栈与队列

栈

栈是什么

栈 是另一种数据结构，其插入 / 删除操作仅能在表的端点进行。

我们将允许进行插入 / 删除操作的一端称为 栈顶 ， 另一端称为 栈底 。
可以看出，栈的操作规则代表着其先进入的元素会被压在栈中，若想删除，则只能等到比其后进入的元素全部删除后才能进行。我们称这种规则为 后进先出 。

栈的基本操作

栈含有以下几种基本操作：

• InitStack：初始化
• StackLength：求长
• GetTop：获得栈顶元素
• Push：入栈
• StackTraverse：遍历
• Pop：出栈
• ClearStack：置空
• StackEmpty：判空
• DestoryStack：销毁

栈的存储结构

顺序存储

我们常用一组地址连续的存储单元来对栈进行存储，即C中的数组。
数组的上界（maxsize）用于表示栈的最大容量，而单独设置一个指针Top用来指向当前栈顶在数组中的位置。

需要注意的是，栈底的位置往往是固定的，但栈顶的位置会随着入栈 / 出栈的操作而变化。

定义如下：

typedef Maxsize n;

typedef struct {
    Elemtype stack[Maxsize];
    int top;
}sqstack;

在这里同时也对栈的各类操作进行一些说明：

初始化

void InitStack(sqstack &s){
    s.top = -1；//直接将栈顶的指针定为-1
}

入栈

Status Push(sqstack &s, Elemtype e){
    if(s.top>Maxsize){
        return ERROR; //此时栈满，即将上溢出
    }else{
        s.top++;
        s.stack[s.top] = e;
    }
}

出栈的操作与入栈相似，只需要考虑是否下溢出即可，这里不再详述。

取顶

Status GetTop(sqstack &s, Elemtype &e){
    if(s.top<0){
        return NULL; //此时栈空
    }else{
        e = s.stack[s.top];
    }
}

其余操作在此不再详述。

基于动态存储的栈管理

上文中基于数组的栈管理方法无法得心应手的进行栈扩容，而由此我们引出基于动态内存管理的方法。

它的定义如下：

# define Stack_Int_Size 100;
# define Stack_Increment 10;

typedef struct{
    Elemtype *base; //指向栈底
    Elemtype *top; //指向栈顶的下一个元素
    int stacksize;
}sqstack;

这样的管理方法使得每次当栈满时，我们可以进行realloc操作重新扩容栈：

if(S.top-S.base>=S.stacksize){
    //栈满，追加存储空间
    S.base = (Elemtype*)realloc(S.base, (S.stacksize + Stack_Incerment)*sizeof(Elemtype));
    S.top = S.base + S.stacksize; //先将栈顶定出来
    S.stacksize += Stack_Increment;
}

需要注意的是，这种定义方法，判断栈满和栈空的语句分别为：

S.top - S.base > S.stacksize; //栈满
S.top == S.base //栈空

多个栈共享空间

在实际运用栈时，我们通常为了节省空间，防止空间浪费，会让多个栈同时使用一片存储空间，这通常表现为分配一个足够大的数组给多个栈，而后利用栈的动态存储特性，来对其进行存储空间的扩充。

以下，对两个栈的空间共享方法进行简要说明：

总体思路在于将两个栈的栈底至于 数组的两端 ，而后在两个栈需要扩充空间时，将其栈顶向数组中间移动。

typedef struct{
    Elemtype stack[m];
    int top1, top2; //分别用于指向两个栈的栈顶位置
} dustack;

如果用指针来表示：

typedef struct{
    Elemtype *m; //整片区域的头指针
    Elemtype *top1, *top2; 
    int stacksize;  //整片区域的大小
} dustack;

这种结构的栈，要判断是否上溢，则需要用到以下语句：

if(top1 == top2-1){
    return ERROR; //上溢
}

这里给出入栈的写法：

void push(int i, int x){
    if(top1 == top2 - 1){
        printf("上溢");
    }else if(i == 1){
        top1++;
        c[top1] = x;
    }else{
        top2--;
        c[top2] = x;
    }
}

链式栈存储结构

在栈的大小并不能确定时，采用链式存储结构能够更加轻松的扩栈，缩栈。

具体在C语言中，即链表的存储方式，但有所不同的是，此处链表的 头结点 指向的是栈的 栈顶 ，因此每次对栈进行操作，相当于是对头结点的位置进行相关的改变。

链栈的定义方式如下：

typedef struct snode{
    Elemtype data;
    snode* next;
} linkstack;

链栈的进栈操作在这里给出：

void push(linkstack top, Elemtype x){
    snode* t = (snode*) malloc(sizeof(snode));
    if(t == NULL){
        return ERROR; //内存满，栈上溢
    }else{
        t->data = x;
        t->next = top; //t的指针域指向原先的头节点
        top = t; //将头结点改成t的位置
        return OK;
    }
}

可以看出，只要内存不爆满，链栈是不会有上溢这种错误出现的，这也是为什么链栈更加灵活的原因。

栈的应用

讲了一堆，现在该看看栈这种后进先出的玩意到底有什么用了

数制转换

算法原理：

N = (N div d)×d + N mod d

其中，d是进制数

举例：
（1348）₁₀ = (2504) ₈
具体计算为：

• 1348/8 = 168; 1348%8 = 4;
• 168/8 = 21; 168%8 = 0;
• 21/8 = 2； 21%8 = 5；
• 2/8 = 0；2%8 = 2；

将每次取余计算的结果逆序链接，则能得到2504的结果

抽象为实现代码即：

void conversion(int i, int N){
    InitStack(S); //初始化一个栈
    while(N){
        //N不得0时，持续循环
        Push(S, N%i);
        N = N/i;
    }
    while(!StackEmpty(S)){
        //栈不空，则循环
        Pop(S, e); //取出栈顶元素，存在e中
        printf("%d", e);
    }
}

需要注意的是，如果涉及到16进制的转换操作，需要对相应的字母与数字之间的关系进行建立，然后再进行算法的进一步优化，这里不再详述

括号检验

在表达式中，括号的对应是十分重要的一环，往往这种工作编译器会帮我们做完，如果需要我们自己进行编写，则需要借助栈这种结构。

如下的括号，都是符合书写格式的：
（ [ ] [ ] ）, ( ( [ ] ) )

但当出现如：
( [ ) ]
这一类的括号时，如何判断其是否符合要求，就是我们的任务。

总结一下，我们在检验括号时，出现的不匹配的现象，往往有三种可能：

• 到来的右括号并不是 被期待的
• 到来的是 不速之客
• 直到最后，被 期待 的括弧也没到来。

由此，我们可以设计出这样的算法：

从表达式左侧开始逐字符扫描，如果遇到左括弧，则入栈。
当遇到右括弧时：

• 如果栈空：则右括弧必定多余，报错
• 如果栈非空，则将右括弧与栈顶元素比较：
  · 如果栈顶元素能与右括弧匹配，则栈顶元素出栈
  · 如果栈顶元素不匹配，则正常入栈

当表达式扫描完成时，如果此时栈空，则表达式无误，若非空，则报错。

行编辑程序问题

如果让我们设计一个输入编辑器，我们应当如何设计？

一个最简单的设计思路是，用户输入一个字符，则存入一个字符。但这样显然是不合理的，如果用户输入错误，我们也应当给用户相应的挽回余地，对吧。

因此，至少需要有退格（backspace）的机制。
这里举一个例子，如果以“#”作为退格符号，用户输入的内容如下：

whli##ilr#e（s#*s)
    putchar(*s=#++);

则有效的输入内容为：

while (*s)
    putchar(*s++);

因此，这种方式十分符合栈的存储方式，思路为：
我们接收到一个字符，如果字符不是退格符，则压入栈顶；
如果字符是退格符，则令一个栈顶元素出栈。

上述例子只是一个最简单的行编辑程序，更多的符号如回车（enter），上档（shift）等可以自行思考。

表达式求值问题

我们向程序中输入一个表达式，我们希望能够输出它的结果，这是如何被计算出来的？

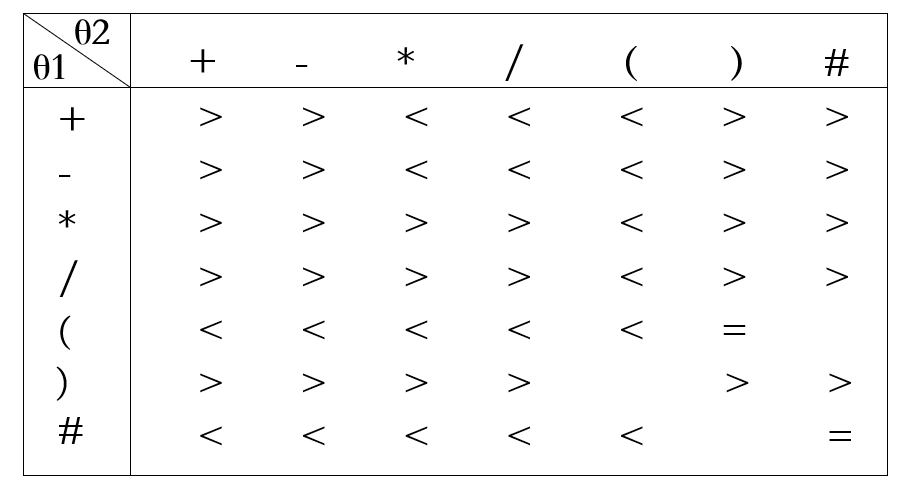
要理解这个问题，我们首先应当介绍一下 算符优先法 。

我们先将一个表达式分成三部分：

• 界限符：即左括号，右括号，表达式终止符等
• 运算符：即算术运算符，逻辑运算符，关系运算符等
• 操作数：常数，变量等

本文中仅仅以简单算术表达式的例子做抛砖引玉作用。（其实是博主水平不够）

要实现这个算法，我们需要设计两个栈，即：

• 运算符栈：OPTR栈
• 操作数栈：OPND栈

算法基本思想如下：

• 我们首先将操作数栈为空栈，将起始符#入栈
• 依次读入字符，如果是操作数，则存入OPND栈，如果是运算符，我们就将当前读入的操作符与栈顶的操作符做优先级比较，并根据比较结果决定要不要进行相关的运算。直到我们的运算符栈里面只有两个#为止。

这里可以看出，相同的运算符，优先级默认是前者大于后者的，这点是为了使得“=”这个优先级仅在括号的判断中出现，防止歧义。

操作符之间的优先级很重要：

• 如果读入的操作符优先级大于栈顶的操作符优先级：则该操作符入栈。
• 如果读入的操作符优先级等于栈顶的操作符优先级：则该操作符必定是括号。
• 如果读入的操作符优先级小于栈顶的操作符优先级：则直接取操作数栈的栈顶两个元素进行运算。

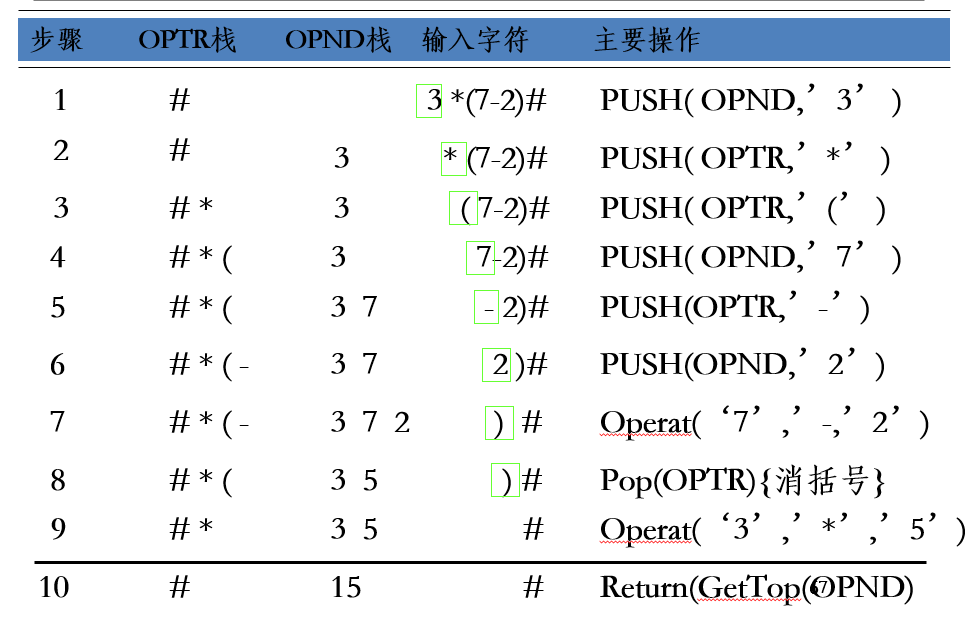
这里给出一个运算式例子：

更多的应用有迷宫求解，递归的实现，地图染色等等，这里不再详述。

队列

只允许在表的一端进行插入，在另一段进行删除的线性表
先进先出

队列的基本操作：

• EnQueue(&Q, e) 入队
• DeQueue(&Q, &e) 出队
• InitQueue(&Q) 初始化
• QueueEmpty(Q) 判空
• DestoryQueue(&Q) 销毁
• QueueLength(Q) 求长
• ClearQueue(&Q) 置空
• GetHead(Q, &e) 求头
• QueueTraverse(Q, visit()) 遍历

顺序存储结构

采用数组进行存储：

typedef struct{
    Elemtype queue(maxsize);
    int front, rear; //front表示队头，rear表示队尾
}queue

入队，改变队尾指针
出队，改变队头指针

队空：

front == rear;

队满：

rear == maxsize;

顺序存储-改进

显然，总有一个时刻，front指针与rear指针均指向数组的maxsize处的元素，但整个数组并没有被填满，反而前面空余了很多空间。这种情况被称为 假溢出 。

假溢出一般有两种解决方式：

• 出队后，令整个队列左移。（涉及大量元素的移动）
• 将Queue[0]接到Queue[maxsize-1]的后方，形成队列环（参考上一章中循环链表的思想）

入队时：

rear = (rear+1)%maxsize;

出队时：

front = (front+1)%maxsize;

这种方法中，还有个问题，即队满和队空的判断语句均为：

front == rear;

对于这个问题，有两种解决方法：

• 可以采用 设置标志位 的方法进行改进：
  队空的情况只能由出队操作引起
  队满的操作只能由入队操作引起
  因此，加一个标志位 flag ，将其初始化为“delete”， 进行入队时，更改其为“enter”。由此判断队空还是队满。

• 可以少用一个存储空间
  这时，队空则仍然由front == rear来判断，队满则可使用front == rear-1的方式来进行判断。

链式存储结构

顾名思义，使用链表对队列进行存储

当然，对于队列的链表而言，我们需要有队头与队尾两个指针来对整个队列进行维护

typedef struct{
    node* front, rear;
}

链队列初始化时，只需要分配出头结点即可，此后利用rear = front来进行初始化
销毁时，从队头开始遍历，分次释放所有的结点

入队：

node* p = (node* )malloc(sizeof(node));
p->data = e;
p->next = NULL;
Q.rear->next = p;
Q.rear = p;

本篇仅对栈和队列的基础定义与一些简单应用做出了阐述，后续有时间会补充更多的细节。

本篇博文就到这里~