数据结构-Chap-5

Data Structure
Study Notes
发布日期:   2023-12-12

数组与广义表

数组

C语言中，我们已经多次接触过 数组 这一概念，这里我们给出数组的具体概念。

数组的定义

在数据结构中， 数组 指有限个数据元素的集合，这些数据元素具有相同的特性，并都有与之相对应的下标来表征它们的位置。

一维数组，与我们在第一章中介绍的 线性表 几乎是同一个东西。但这里，我们数组的维数理论上可以无限延申。

但向外延伸的复杂度则也带来了些许不便，即数组的删改操作会变得极其复杂（尤其在维数过多的情况下），因此我们不妨一刀切掉，数据结构中定义的数组，除了初始化与销毁两种操作之外，只有两种运算：

  • 给定下标，存储相应的元素
  • 给定下标，修改相应下标内元素的值

很多读者可能会想起C中的relloc操作，但relloc操作常见于一维数组，即线性表的范畴内，因此这里不再对数组的删改进行叙述。

数组的基本操作

如上所述，数组仅仅包含以下几种操作：

  • InitArray：初始化
  • DestroyArray：销毁
  • Value：取出数组的元素值
  • Assign：给数组赋值

数组的顺序表示

以二维数组为例

数组既然是多维的，则必然存在存储顺序优先级的问题，由于普遍已经适应了 以行序为主序 的存储方法，因此本文中会采用行序主序的映像方式进行说明。

上面的说法有点抽象，举个例子：
存在一个2*3的数组，如果使用行序主序的方式，则在计算机内存中的存储顺序即：0 0、0 1、0 2、1 0、1 1、1 2。
相反的，如果使用列序主序的方式，则在计算机内存中的存储顺序即：0 0、1 0、0 1、1 1、0 2、1 2

因此，一个m行n列的数组采用行序主序的形式时，存储aij的位置时，其位置即：

LOC(i, j) = LOC(0, 0) + (n*i + j) * L;

如果以列序为主序，则：

LOC(i, j) = LOC(0, 0) + (m*j + i) * L;

这里，LOC(0, 0)被称为基地址（即数组第一个元素所在的地址），L则是数组一个元素所占有的内存大小。

矩阵相关

了解过高等数学的读者可能看出来了，我们拿来举例子的二维数组，在数学上有个另外的名字，叫 矩阵 。

但我们又想了，这矩阵里面可能有很多 值相同的元素 或 0元素 ，显然，它们用处不大，但是占据了很大一部分的存储空间，这就显得很浪费。因此，我们需要研究一下压缩存储的相关问题。

那首先，我们讨论一下压缩的基本规则：

  • 多个值相同的元素，我们只分配一个存储空间
  • 0元素，我们不分配存储空间

我们先看一些特殊的矩阵：

对称矩阵的压缩存储

对称矩阵 ，即 aij = aji ，我们可以只为每对对称的元素分配一个存储空间，即我们可以只存储其下三角（包括对角线）中的元素。

说的详细点，在内存中的下标存储方式：0 0、1 0、1 1、2 0、2 1、2 2、……、n-1 0、n-1 n-1。

由这个规律，我们得出对称矩阵压缩存储时其下标计算公式：

LOC(i, j) = LOC(0, 0) + [i*(i+1)/2 + j] * L;

i*(i+1)/2 是一个从1到i，公差为1的等差数列的求和公式，读者自己推一下即可。

三角矩阵的压缩存储

三角矩阵 即一个矩阵中只有其上（下）三角的位置有元素，其余部分为0元素或常数C。

因此，其实与对称矩阵非常类似，我们留出相应的三角矩阵的存储空间，而后增加一个存储常数C的存储空间即可

稀疏矩阵相关

稀疏矩阵 即矩阵中零元素的出现没有规律的矩阵

在了解它如何压缩之前，我们先来了解一个概念—— 稀疏因子 。
其定义为如果m行n列的矩阵中含有t个非零元素，我们称：

d = t / m*n

为稀疏因子，即数组中非零元素个数与非零元素个数的比。

如果这个稀疏因子的大小小于0.05，则我们称这个矩阵为稀疏矩阵。
这种稀疏矩阵造成了两种问题：

  • 零元素占据空间过大
  • 进行运算时（除法 / 取余），需要频繁的判断当前的除数是否为0

这就代表着压缩存储的操作非常的必要

三元组表示法

这种压缩方法大概是最容易想到的了，即我们用一个线性表来表示稀疏矩阵，这个线性表中每个元素都是一个结构体，结构体里有三个元素，分别为非零元素的行下标、列下标、值。

相应的，习惯使然，我们在存储它时也已行下标优先的存储方法。

typedef struct{
    int i, j; //行、列下标
    Elemtype v; //非0元素的值
}Triple;

typedef struct{
    Triple data[Maxsize+1];
    int line, col, num; //矩阵的行数、列数、非零行个数
}TSMatrix;

三元素表示法的加、减都挺简单，但一旦涉及到矩阵的 转置 ，则事情就变得有些复杂。

  • 三元组的转置——常规转置

我们知道，常规矩阵的转置：

for(int i = 0;i<line;i++){
    for(int j = 0;j<col;j++){
        swap(a[i][j], a[j][i]);
    }
}

放到三元组里面，我们可以采如下的转置方法：

  • 将矩阵的行、列值互相调换
  • 将三元组存储行、列下标的变量互换
  • 将三元组重新排成以行序为主序的顺序表

这前两步非常简单，但第三步的实现需要琢磨一下，我们这里也给出两种方法：

  • 按照原先三元组列序的顺序查找（因为原先三元组的列序就是转置后三元组的行），而后按照顺序进行转置，转置后依次添加进一个新的三元组里面。
  • 直接按照原先三元组中的顺序进行转置，此后将转置的每个元素置入与之对应的新位置里。
//第一种方法
Trans(TSMatrix M, TSMatrix &N){
    //M是需要被转置的矩阵，N是一个全新的矩阵
    if(M.num!=0){
        //M非空
        N.line = M.col;
        N.col = M.line;
        N.num = M.num;
        int temp = 1;
        for(int col = 1; i<M.col; i++){
            for(int line = 1; j<M.line;j++){
                //从M的第一列开始转置
                if(M.data[temp].j == i){
                    N.data[temp].i = M.data[temp].j;
                    N.data[temp].j = M.data[temp].i;
                    N.data[temp].v = M.data[temp].v;
                    //行列互换，值直接赋入新三元组
                    temp++;
                }
            }
        }
    }
}

第一种方法非常清晰明了，但是显然效率不够，因为我们需要将三元组所有的元素都扫描很多遍，这显然不是很优雅。

这种转置方法存在循环的嵌套，因此其时间复杂度为：

O(M.num * M.col);

我们再想一想，我们如果能知道M中每一列的 第一个非零元 在N中应该存储的位置，那么我们在对M中的元素进行转置时，我们就可以直接将相应的元素放到N中合适的位置上，这就显得非常的理想。

问题来了，这法子需要怎么实现呢？

  • 三元组的转置——快速转置

我们想知道新矩阵每一行开始的位置，我们自然需要对原数组先进行一次遍历，通过这次遍历的结果得到我们想要的数据并进行储存。

因此，我们再设置两个数组：

nums[col] //表示原矩阵中第col列中含有多少个非零元素
cpot[col] //表示原矩阵中第col列的第一个非零元素在新矩阵中的起始位置

注：这里需要再啰嗦一嘴，原矩阵中的第col列其实就是新矩阵中的第col行，因此cpot[col]中的元素就是新矩阵里面第col行的起始下标。

我们可以通过以上的关系得到这个式子：

cpot[1] = 1; //第一行的第一个非零元的起始下标为1
cpot[col] = cpot[col-1] + nums[col-1]; //第col行的第一个非零元的起始下标 = 上一行的起始下标 + 上一行的元素数

如果将上述式子写成代码也非常简单，只需要用for循环遍历一遍，就能将nums数组中的所有元素得到，而后再通过nums遍历一遍得到cpot数组即可：

得到这个cpot数组后，转置的工作就很简单了，这里给出具体的转置代码：

//第二种方法
Trans(TSMatrix M, TSMatrix &N){
    if(M.num!=0){
        //M非空
        N.num = M.num;
        N.line = M.col;
        N.col = M.line;
        int* nums = (int*) malloc(sizeof(int)*(M.col+1));
        int* copt = (int*) malloc(sizeof(int)*(M.col+1));
        //这里之所以每个数组都多分配一个空间是因为想让下标从1开始，与三元组统一
        for(int i = 1;i<M.col;i++){
            nums[i] = 0;
        } //初始化nums数组
        for(int i = 1;i<M.num;i++){
            nums[M.data[i].j]++;
            //遍历M中每一个元素，该元素是哪一列，就把nums相应下标的值+1
        } //nums数组赋值完成
        cpot[1] = 1;
        for(int i = 2;i<M.col;i++){
            cpot[i] = cpot[i-1]+nums[i-1];
            //通过遍历得到cpot每一个值
        } //cpot数组赋值完成

        for(int p = 1;p<M.num;p++){
            int col = M.data[p].j;
            int place_in_N = cpot[col] + M.data[p].i;
            //在新三元组N中的下标为：行起始下标+新矩阵中的列下标（也就是原矩阵中的行下标）
            N.data[place_in_N].i = M.data[p].j;
            N.data[place_in_N].j = M.data[p].i;
            N.data[place_in_N].v = M.data[p].v;
            //行，列下标互换，值不变
        }
    }
}

上述完整方法其实理解起来有一定难度，主要是因为需要定义以及捋清楚的变量非常多，如果读者暂时无法理解全部，也可以先放一放，或者跟着此前的梳理顺序再来一遍。

我们再来看这个算法的时间复杂度：

我们通过分别对M的列以及M的所有元素进行遍历，实现了这个算法，其时间复杂度为

O(M.num + M.col);

这个加式可比之前那个乘方式好看多了

行逻辑链接表示法

三元组表示法的优点在于其内每个非零元素的行下标与列下标都非常清晰，可以直接提取出来，但是如果我们需要随机存取某一行中的非零元，则三元组需要从头开始遍历，不是非常的优雅。

我们参考三元组快速转置中的思路，直接将一个数组rpos添加到压缩后矩阵的结构体的定义中，其代表的就是每一行第一个非零元在三元组中的下标。

typedef struct{
    Triple data[Maxsize+1];
    int line, col, num; //矩阵的行数、列数、非零行个数
    int* rpos = (int*) malloc(sizeof(int)*line);
}RLSMatrix;

这样的话，我们如果给定一组下标(r, c)，我们就可以直接通过以下的算法进行取值：

Elemtype value(RLSMatrix M, int r, int c){
    //r:行数; c:列数
    int p = M.rpos[r];
    while(M.data[p].i == r && M.data[p].j < c){
        p++;
    }
    if(M.data[p].i == r && M.data[p].j == c){
        return M.data[p].v;
    }else{
        return 0;
    }
}

行 / 列链接存储表示法

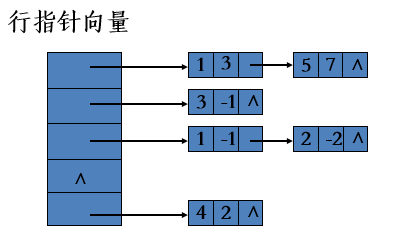
如果我们想用指针来对稀疏矩阵进行存储，思路也很简单：
我们可以以每行 / 每列为单位，存储一个链表的头节点，在其后面存储每一个不为0的元素为一个节点。

这里以行链接表示法为例，给出具体定义：

typedef struct LinkNode{
    Elemtype v;
    int col // 每一个元素的列数
    LinkNode* next;
};

typedef struct CpMatrix{
    int num, line, col;
    LinkNode* Head; //链表的头指针
};

用图示表示一下：

行链接存储

看到这里，有些读者可能就有些 大胆的想法 ，哎？我如果行与列都加上一个链表来存储呢？当然可以，不过这种玩意维护起来就显得有亿点点麻烦了，有需求的读者可以自行尝试实现，这里权当抛砖引玉。让我们在读者的思想变得更危险之前进入下一个话题…

广义表

广义表这个玩意其实目前用的已经很少了，因为它的定义方式决定着这玩意哪怕是用手画都很难理解，并且捋清楚层次，更别提用真正的计算机来实现它了，其实这玩意的思路跟后面要叙述的 多叉树 非常的接近，占用空间又比树大，所以嘛…

说了这么多，毕竟这玩意也是数据结构的考点，还是在这里大体捋一下。

广义表 是用递归形式定义的线性结构，是线性表的推广，它的元素可以是一个单元素，也可以是一个子表。

LS = (α1, α2, α3, …, αn);

以上是它的书写形式，LS是其表名，而其中的α1, α2 等元素，可以是一个元素，也可以是又一个表 （这不纯纯tm套娃吗）

上面的定义决定了广义表这玩意有以下性质：

  • 广义表里的元素是有顺序的
  • 广义表的长度：最外层的表含有的元素个数
  • 广义表的深度：广义表所含括弧的重数，即其最深的一枝能深到第几层
  • 广义表可以是递归的

广义表的分解

这里咱单开一块来说一说广义表分解这一茬事情，因为这玩意的定义方式使得分解很容易把人绕晕喽。

我们通常认为，任何一个广义表，都可以被分解成表头和表尾：

  • 表头是广义表的第一个元素
  • 表尾是广义表的 剩余元素组成的新广义表

请希望学习这一部分的读者提高重视，表头是一个元素，而表尾必定是一个 广义表 。这个分解方式在学习时已经坑了笔者很多次了，希望读者能够不要像笔者一样踩这么多坑。

我们举个例子：
有个广义表：

D = (E, F);
其中E = (a, b, c); F = z;

那么 D的表头 就是 E ，而 D的表尾 是 (F) 。
再写一个，加深一下印象：E的表头 是 a ，而 E的表尾 是 (b, c) 。

在读者能够清晰地分辨出表头和表尾的区别后，我们进入下面的章节。

广义表的表示

由于广义表的定义过于复杂，拆解也很复杂，因此广义表的表示通常只能用链表这一结构来实现。

我们首先明确一下，广义表中，存在两类节点：

  • 表节点（表示这里面是另一个表）
  • 原子节点（表示这里面只有一个元素）

这两类节点通过一个额外的表示符 tag 来区分。

我们这里只说一种表示方法

表头、表尾分析法

这法子挺自然的，刚刚说了拆分方式嘛，所以我们干脆直接将节点中拆出两个玩意来，一个指向表头，一个指向表尾。

typedef struct GenNode{
    int tag = 1; //表节点
    GenNode* ListHead, ListTail; //分别指向表头以及表尾
}GenList;

typedef struct Atom{
    int tag = 0; //原子节点
    Elemtype value;
};

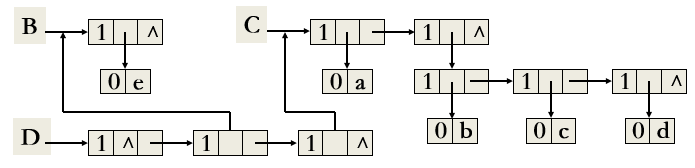
这里举一个相对复杂的例子来让读者再次理解这个分析的方法

A=( ) ; B=(e) ; C=(a,(b,c,d)) ; D=(A,B,C)

我们把D用这种方法来表示出来：

D 表头表尾分析法

可以得见，这玩意真要表示需要耗费多少空间…

其实这玩意还有另一种表示方式叫 子表分析法 ，这种法子相对而言比较节省空间，但是把这玩意写出来的话想必读者会更混乱，这里有需求的读者可以自行查阅其他资料。

广义表的相关算法

这里我们只写一个广义表求深度的算法，我们利用递归的思想来求一个广义表的深度：

int GetDepth(GenList L){
    if(L == NULL){
        return 1; //L是空表，深度为1
    }
    if(L.tag == 0){
        return 0; //L是原子节点，返回深度0
    }
    GenNode* p = &L;
    int max;
    for(max = 0; p; p = p->ListTail){
        int dep = GetDepth(p->ListHead);
        if(dep > max){
            //当前表头的深度比此前得到的深度更深
            max = dep;
        }
    }
    return max+1;
}

至此，数组与广义表的内容就阐述的差不多了。

额外提一嘴，广义表的相关概念，考虑到日常生活中的应用概率较低，可以不必过于在意，但如果是因为数据结构考试的话，建议还是深入思考一下（苦笑

好啦，这篇博文就到这里~

文章作者: MUG-chen
文章链接: http://mug-chen.github.io/posts/6435.html
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 MUG-chen !
Data Structure
  目录