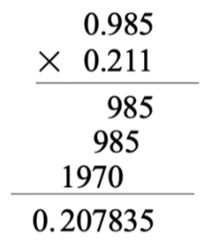发布日期: 2025-02-23

更新日期: 2025-03-20

文章字数: 11.9k

计算机组成原理 Chap.2 数据的表示和运算

本系列计算机组成原理博文基于Bilibili王道计算机教育的免费考研课程整理而来, 目的在于系统的梳理计算机专业课的基础知识, 并为将来的面试做好充分的准备.
除本系列外, 计算机考研相关还包括数据结构 / 操作系统 / 计算机网络的相关内容. 会在后续时间内一一进行补足.

2.1 计算机中的进制以及数的表示

第一章中我们寻思了计算机的基本组成结构以及一些总体性的玩意, 这一章我们率先进入一个大难点, 运算 .

聊到运算, 首先要唠唠这个进制的事.

2.1.1 进位计数制

进制 , 这是个挺古老的概念, 这玩意最开始要追溯到罗马数字了, 但我们这里不唠太多有的没的, 仅仅给出一些重要的概念和方法.

概念: 基数
每个数码位所用到的不同符号的个数. 十进制的基数就是10, 二进制的基数就是2.

我们在计算机中通常只涉及到四种常用的进制:

二进制 : $ (1010)_2 / 1010B $
八进制 : $ (534)_8 $
十进制 : $ (534)_{10} / 534D $
十六进制 : $ (a145)_{16} / a145H / 0xa145 $

注意: 进制的表示方法
二进制的 B 来源于英文 Binary ; 十进制的 D 来源于英文 Decimalism ; 十六进制的 H 来源于英文的 Hexadecimal .

二进制 是最适合计算机进行信息存储与处理的的进制, 这主要有3方面的原因:

仅需要 两个稳定状态 的物理器件就能表示全部的信息
0 / 1 刚好对应计算机中的逻辑 假 / 真 , 方便实现逻辑运算
算术运算可以很方便的使用逻辑门电路实现

扯远了, 我们拉回来点. 进制知道了, 那自然要涉及到 书同文 这么一个事情, 互相转换要整的明明白白的.

对于 二进制 / 八进制 / 十六进制 转 十进制 这个事情, 我们通常采用 位权相乘 的方式, 即 位上的数值 * 对应位的权重值

例子
以常见的16进制举例:
16进制转10进制: $ 123.12 = 1 \ast 16^2 + 2 \ast 16^1 + 3 \ast 16^0 + 1 \ast 16^{-1} + 2 \ast 16^{-2} $

这之后, 我们要考虑 二进制 / 八进制 / 十六进制互相转换 的问题. 这个玩意的原理挺简单的, 是由它们基数之间的关系得到的: $ 2^3 = 8, 2^4 = 16 $ , 因此我们很自然的想到应该能实现 三个2进制数能与一个8进制数互相转换 , 四个2进制数能与一个16进制数互相转换 .

注意: 转换的补零
由于这种转换方式的起始点是 小数点 , 因此当某组位数不足时, 需要自动在前 / 后补零.

例子
二进制数: 10 011 101 . 101 01
八进制数: 235 . 52

最后是 十进制转二进制 / 八进制 / 十六进制 的问题. 这个问题的方法是通过上面的 位权相乘 式子得来的. 有想法的读者可以自己举个例子证明一下, 原理很简单.

十进制的转换要分整数部分和小数部分分别写. 整数部分的处理方法为 除基取余 , 将每次除完的余数从小数点开始往前写. 小数部分的处理方法为 乘基取整 , 将每次相乘后的整数位从小数点开始往后写.

转换整明白了. 我们最后出两个概念: 真值 / 机器数 .

这个问题的根源在于数字这玩意很讨厌, 它有正负, 但是机器上只能通过二进制来表示一个数, 这就意味着必须要单独分一个位来表示这个数是正值还是负值.

例子
真值: +15
机器数: 0 1111 (最前方为符号位, 0表示正)

2.1.2 定点数的编码表示

这标题有点突兀, 定点数 是个啥玩意?

概念: 定点数 / 浮点数
定点数 , 指的是在表示数据时, 小数点的位置是固定的. 举例而言即 996.007 .
浮点数 , 与之对应, 即在表示数据时使用科学计数法的方式将数据拆为两部分. 举例而言即 $ 9.96007 \ast 10^2 $ .

这么看定点数还挺简单的, 直接写就完了? 理是这么个理, 但由于计算机里面要进行运算的类型不同, 在 有符号数 的定点表示部分, 我们还需要接触些新的内容.

2.1.2.1 无符号数的定点表示

概念: 无符号数
指的是整个机器字长的全部二进制位都是数值位, 没有符号位 .

无符号数的表示原理挺简单的, 因为不涉及到符号位. 我们这里只需要明确其 表示范围 即可.

n位无符号 数的表示范围: $ 0 \sim 2^n -1 $ .

注意: 无符号数的修饰范围
通常而言, 无符号数不会用于修饰浮点数, 而仅仅会用于修饰整数.
例如, 在C语言中, 无符号的修饰符 unsigned 仅能够用于修饰 int, long long 等整数类型.

2.1.2.2 有符号数的定点表示

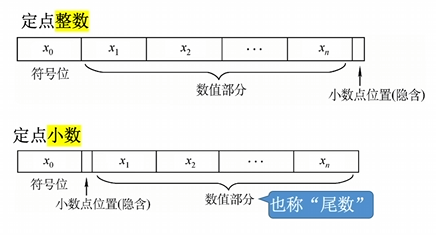
既然是定点, 通常来说整数和小数就要分开保存了.

可见, 所谓定点就是将小数点定在了 整数之后 以及 小数之前 . 符号位则永远处于最前面的位置, 除了符号位以外用于表示数值的部分, 我们单独起个名叫尾数 .

明确完这种表示方法, 我们要唠唠一个老大难问题: 原码 / 反码 / 补码 / 移码 .

原码 , 即用尾数表示 真值的绝对值 . 这种表示方法是最简单易懂的, 它最符合我们印象中的二进制表示, 只不过单加了一个符号位而已.

例子
+19D
定点整数: 00010011
注: 上文中将符号位用特殊颜色标出. 实际书写时也有 在符号位后加一个逗号 这种习惯. (0,0010011)

现在考虑一下 原码的表示范围 :

对于 n位定点整数 而言, 由于其尾数(n-1位)其实就是无符号数的表示方法, 因此加上符号位的表示范围: $ -(2^{n-1}-1) \leq x \leq (2^{n-1}-1) $ .

注意: 原码中的0
0在原码中由于符号位, 可以被分为 +0 / -0 两种形式. 这也是为什么我们用n-1位, 只表示出了 $ 2^{n-1} -1 $ 个数的原因.

对于 n位定点小数 而言, 我们还是先看尾数(n-1位), 全0为最小值, 全1为最大值, 计算出n-1位尾数能表示的范围: $ 0 \sim 1-2^{-(n-1)} $ .

然后我们再加上符号位, 得到n位定点小数的表示范围: $ -(1-2^{-(n-1)}) \leq x \leq (1-2^{-(n-1)}) $ .

反码 , 定义如下:

若 原码为正 , 则该数的反码等同于该数的原码.
若 原码为负 , 则该数的反码是该数原码 除符号位以外各位取反 的结果.

例子
-19D
$ [x]_原 $ = 10010011
$ [x]_反 $ = 11101100

可见, 原码和反码是 一一对应 的关系. 因此在表示范围上, 反码和原码是相同的.

注意: 反码中的0
有原码的转换得知反码中 +0 / -0 的表示:
$ [+0]_反 $ = 0,0000000
$ [-0]_反 $ = 1,1111111

反码只是由原码转向补码的一个中间状态, 在实际应用中并没有什么作用.

补码 , 定义如下:

若 原码为正 , 则该数的补码等同于该数的原码.
若 原码为负 , 则该数的补码为该数 反码的末位+1 .

例子
-19D
$ [x]_原 $ = 10010011
$ [x]_反 $ = 11101100
$ [x]_补 $ = 11101101

注意: 补码中的0
有兴趣的读者可以自行看一下-0转成补码之后的形式, 它会进位出一个范围外的1被系统丢弃, 因此 +0 / -0在补码中的表示是相同的 .

那问题来了, 原来原码和反码都用了两种情况表示0, 你补码把其中一种情况(1,0000000)丢了, 咋整捏?

因此, 对这种特殊情况做出了特殊规定, 还是拿8位机器码举例:

在 定点整数 中: (1,0000000)用于表示 $ -2^7 $
在 定点小数 中: (1,0000000)用于表示 $ -1 $

这意味着, 相比于原码和反码, 补码可以多表示一个负数 , 对于定点整数, 其表示范围为: $ -(2^{n-1}) \leq x \leq (2^{n-1}-1) $ ; 对于定点小数, 其表示范围为: $ -1 \leq x \leq (1-2^{-(n-1)}) $ .

注意: 补码转原码
正常而言, 我们应该先把加进去的1减掉, 然后逐位取反对吧. 但这里是二进制, 因此其实我们按照原码转补码的方式(除符号位各位取反再+1)再操作一遍, 就是补码转原码了.

移码 , 定义即:

在补码的基础上, 将其符号位取反 . ~~(是的, 没有额外的规定了)~~

注意: 移码的表示范围
移码只用来表示整数.

由于移码是由补码转换而来的, 因此移码和补码的数的表示范围也是相同的.

关于 移码的作用 , 我们这里简单提一嘴:

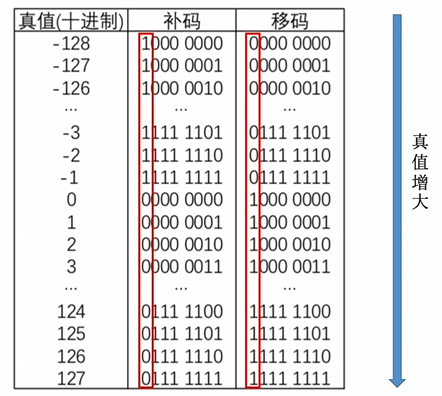
对比一下补码和移码, 可以发现 ~~补码这叫一个乱七八糟~~ , 把移码当作无符号数来看的话, 正好是真值越大, 对应的无符号数越大.

因此移码可以很方便的实现整数的大小比较.

各种码制, 我们唠完了, 但是这一堆有啥用? 我们待会说.

2.1.3 补码的作用

搞了这么多乱七八糟的玩意有啥用呢?

举个简单的例子, 我们用有符号数来表示 +14 + (-14) , 如果直接用原码摁算, 结果显然不是0.

$$
\begin{align*}
\space \space \space 00001110 \\
+\space 10001110 \\
Result \space 10011100
\end{align*}
$$

这种情况挺不符合直觉的, 按理来说这玩意应该直接得到0对吧.

事实上, 我们应该在符号位不同时 对尾数运用减法 , 可以有效地解决这一问题. 但问题又来了:
他娘的减法器比加法器可难设计多了 .

好嘛, 最终有一帮子人寻思着能不能把减法也用加法整出来, 所以搞出了上面那一坨.
这个事怎么实现呢, 得从模运算说起.

上面我们提到了, 计算机能表示的数字再大, 也有那么个上限. 因此实际上, 我们将数字14变成0, 并不仅仅只能用减法来实现, 我们可以 直接把它加到上限, 然后进行一个取模运算 .

概念: 补数
在数论中, 指的是两个数相加之后等于模数的情况.

所以, 减去某个数, 实质上等价于 加上这个数的补数 . 现在问题是, 补数怎么求?

我们上个小节说了个玩意叫补码 . 对, 就那么求.

现在读者应该明白为啥正数的补码就是它自己了, 因为正数相加的时候根本不需要什么转换, 只有涉及到负数的时候才需要有求补这一步 .

2.1.4 零扩展 / 符号扩展

不整啥复杂的了, 直接上概念:

概念: 扩展
指的是从小位宽数据向大位宽数据进行转换. 简单而言就是16位数据转到32 / 64位数据的过程.

为啥要扩展? 因为不同的数据之间的运算都需要借助 ALU 进行实现, 但ALU能接收的数据宽度是固定的. 因此首先就需要进行一个统一位宽的工作.

所谓 零扩展 和 符号扩展 是两种扩展的方法. 适用于不同的情况.

零扩展 , 适用于无符号整数(unsigned), 这是因为这玩意不受到正负号限制, 因此扩展时只需要 在高位补零 即可.

$$ 01011010 \to 00000000 \space 01011010 $$

符号扩展 , 适用于带符号整数(short, char, int, longlong, …), 这一类整数在计算机中往往以补码的形式进行存储, 在符号位扩展时要遵守的原则为 用符号位扩展高位 .

$$ 1,1011010 \to 1, 11111111 \space 1011010 $$

2.2 计算机中的四则运算

2.2.0 数字电路基础知识补充

关于最最基础的 与或非 运算等知识我们这里不再细说了, 这是数字电路中最最基础的内容. 对此部分不了解的读者请自行查找 逻辑运算 / 逻辑门电路 相关的内容.

本小节主要目的在于补充几个比较重要的部件.

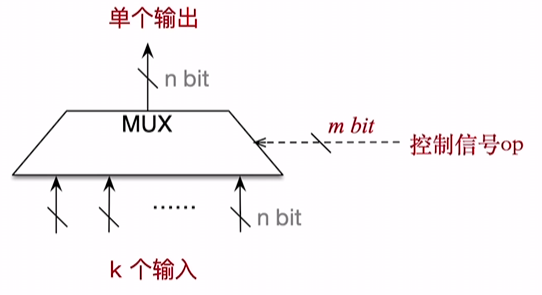
多路选择器(Multiplexer, MUX)

该部件的作用是在 多个输入中根据控制信号OP的值来选择一个输入让其输出 . 控制信号的位数是有长度要求的: $ m \geq log_2k \space bit $ . (因为m位信号最多能表示 $ 2^m $ 种可能)

注意: 多路选择器的预留控制信号
上面提到的情况是该选择器总有一个信号能够通过, 但实际情形中有可能会 单独预留一个控制信号 , 并将该控制信号单独作为 拦截所有输入的信号(没有一种输入可以通过) .
最简单的方式及将m扩展一位, 并选择一个不存在的输入作为控制信号即可.

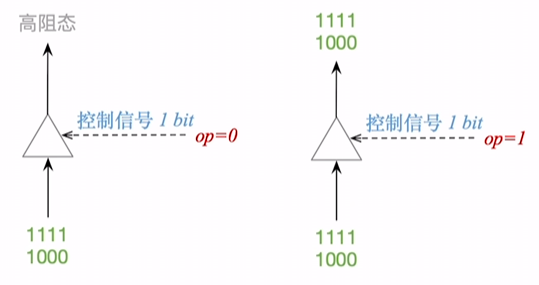
三态门(tristate portal)

跟上面的多路选择器类似, 但只有一个输入. 当控制信号OP=0时, 呈现高阻态, 阻止数据通过, 否则则原样传递数据.

注意: 高阻态
高阻态相当于直接把这个电路给 断掉了 , 它并不属于高电平 / 低电平这两种状态之一.

2.2.1 实现运算的硬件单元

我们先来唠一唠在计算机里面是用什么硬件来实现这些四则运算的.

2.2.1.1 加法器

加法器的目的在于实现 由加数A, 被加数B得到和S 的过程.

咱一步步来, 先看对于一位二进制位, 加法器需要有什么:

被加数的本位 $ A_i $
加数的本位 $ B_i $
来自低位的进位 $ C_{i-1} $
本位和 $ S_i $

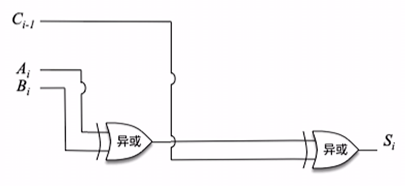
这几位之间的关系可以用如下的式子表示:

$$
\begin{align}
& S_i = A_i \oplus B_i \oplus C_i \tag 1 \\
& C_i = A_iB_i + (A_i \oplus B_i)C_{i-1} \tag 2
\end{align}
$$

这俩式子我们解释一下:

(1) 意味着输入中只要有奇数个1就输出1
(2) 意味着输入中至少有两个1时就输出1

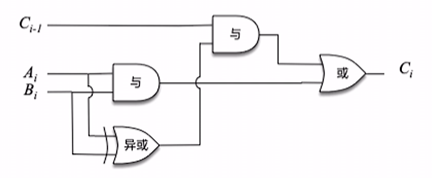
然后给一下这俩式子对应的逻辑电路:

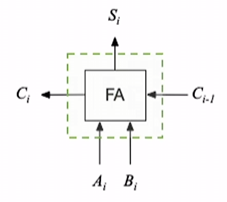
把这俩电路封装一下, 仅仅暴露出输入 / 输出的接口:

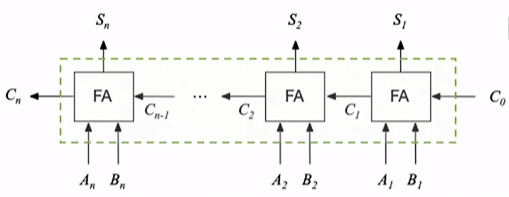
一位搞定了, n位就不足为惧了, 把n个这样的玩意拼到一块去, 然后把进位的玩意连起来就完事了嘛.

我们一般称呼这种加法器为 串行进位的并行加法器 .

概念: 串行进位的并行加法器
指并行数据输入, 但串行进位的加法器.

好的, 这一步步的推下来贼顺溜, 但是问题来了, 这么进位可太慢了.

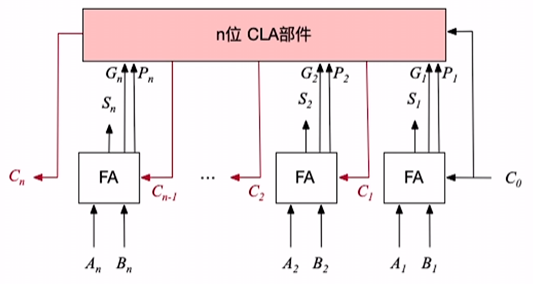
我们的目标现在更高了, 我们希望搞出一个能在数据输入的同时就得到所有进位信息的加法器, 即 并行进位的并行加法器 .

概念: 并行进位的并行加法器
指并行数据输入, 同时并行进位的加法器.

这个玩意的原理我们先不深究, 我们本节中就知道这东西是刚刚的加法器加上 CLA部件 改造而来的就成了.

倒腾到现在, 我们的运算速度算是搞上去了, 随后需要再添加一些小细节.

判断加法器工作后是否溢出.
判断加法器结果是否为0 (A == B ?)
判断加法器结果的正负 (A > B ?)

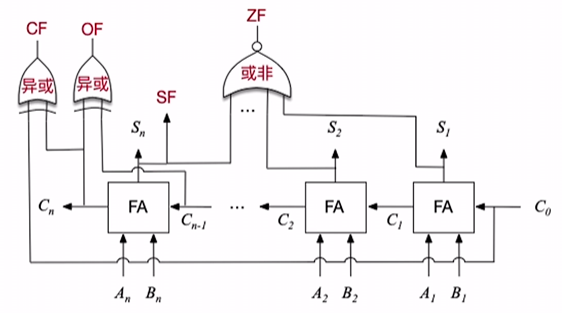
根据我们上面的需求, 给这个加法器加点标志位:

OF(Overflow Flag) : 溢出标志, 用于判断 带符号数 加减运算是否溢出(1表溢出, 0表未溢出)
SF(Sign Flag) : 符号标志, 用于判断 带符号数 加减运算结果的正负性(1表负, 0表正)
ZF(Zero Flag) : 零标志, 判断加减运算结果是否为0(1表结果为0, 0表结果非0)
CF(Carry Flag) : 进位 / 借位标志, 用于判断 无符号数 加减运算是否溢出(1表溢出, 0表未溢出)

$$
\begin{align}
& OF = C_n \oplus C_{n-1} \tag 1 \\
& SF = S_n \tag 2 \\
& ZF = \overline{S_n + … + S_2 + S_1} \tag 3 \\
& CF = C_{out} \oplus C_{in} = C_n \oplus C_0 \tag 4
\end{align}
$$

这里面比较难理解的是 (1) 和 (4) , 我们暂且按下不表, 等到后面了解到具体的运算过程中来解答.

2.2.2.2 快速进位

我们上一节说除了串行进位还有个并行进位的玩意, 那东西可快. 但是并行进位怎么实现呢?

得从我们之前写的进位公式说起:

$$ C_i = A_iB_i + (A_i \oplus B_i)C_{i-1} $$

这东西我们细细一寻思, 嘿, 是个递推.

这就代表着这玩意能接着往下拆:

$$
\begin{align}
& C_i = A_iB_i + (A_i \oplus B_i)C_{i-1} \tag 1 \\
& C_i = A_iB_i + (A_i \oplus B_i)(A_{i-1}B_{i-1} + (A_{i-1} \oplus B_{i-1})C_{i-2}) \tag 2 \\
& … \tag 3
\end{align}
$$

这意味着我们要算 $ C_i $ , 需要的信息是:

$ C_0 $
$ B_0, B_1, …, B_{i-1} $
$ A_0, A_1, …, A_{i-1} $

这一堆东西就好拿了, 意味着其实后面的进位可以直接在运算一开始直接得到.

但这种情况还有个问题, 这东西套两位就挺复杂的, 这要套64位, 好家伙, 开玩笑呢.

这就产生了另一种方式, 即 组内并行, 组间串行 , 即将位数分组(通常是4位一组), 随后组内的进位立刻算出, 组外的运算需要等上一组的进位结果产生后再进行计算.

当然, 这种方式的原理与此前的两种加法器就大同小异了, 也不太算是一个很重点的玩意, 这里就不再详述.

2.2.1.3 算术逻辑单元ALU

ALU, 英文全称 Arithmetic and Logic Unit , 翻译为 算术逻辑单元 .

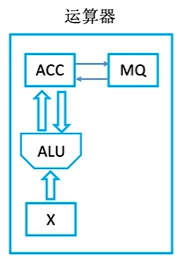
考虑我们在第一章中提到的内容: (专业课总复习-计组-Chap.1)

得见, ALU是运算器中很重要的一部分. 它负责对各种寄存器中的数据进行处理与运算, 得出结果.

注意: 运算器中的核心
由于ALU负责各种算数运算和逻辑运算的实现, 因此 ALU是运算器的核心 , 此外, 后续章节中我们会了解到, 各种算数运算都是途径加法器而实现的, 因此 ALU的核心是加法器 .

ALU主要实现的功能有以下三类:

算数运算 : 加减乘除
逻辑运算 : 与或非, 异或, 移位
其他 : 求补, 直送, …

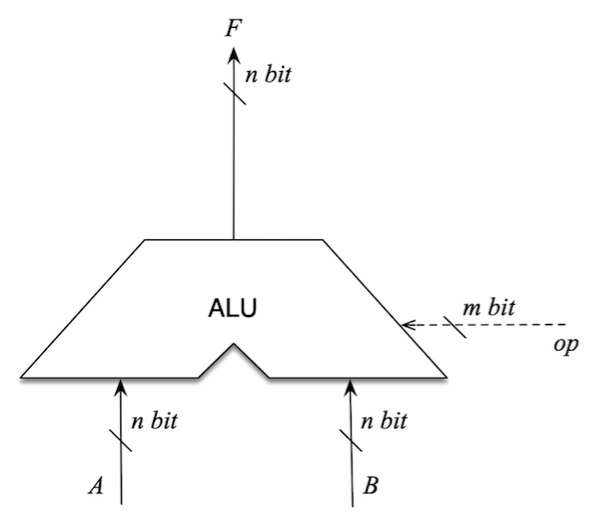
ALU的输入端即上图中的 $ A, B $ , 而功能控制则交与控制信号 $ op $ 进行控制.

注意: 控制信号的位数
控制信号 $ op $ 的位数是跟ALU的功能总数密切相关的, 具体而言, $ |op| \geq \lceil log_2k \rceil $ , 其中 $ k $ 为ALU的功能总数.
读者可能觉着这玩意跟之前提过的一个叫 多路选择器MUX 的玩意挺像, 哎, 很对, 在MUX的前面接上对应的功能电路, 再在每个功能电路前接上输入, 它不就是一个简单的ALU嘛.

此外, ALU除了F之外正常还能输出之前提到的四个标志位: 0F, SF, ZF, CF , 这些标志位信息能够进一步送到运算器的某些寄存器(比如PSW, 又称FR(Flag Register)寄存器)中供CPU取用.

2.2.2 定点数的移位运算

唠完了硬件, 我们来唠唠几个运算. 首先从移位运算开始.

概念: 移位
通过改变各个数码位与小数点的相对位置, 从而改变各个数码位的位权.
说的简单点就是乘 / 除对应的基数.

移位运算通常分三类:

算术移位
逻辑移位
循环移位

2.2.2.1 算术移位

我们直接从例子开始:

例子
-20D
$ [x]_原 $ = 10010100
右移一位 等价于 $ \div 2^1 $
$ [x’]_原 $ = 10001010

可见, 原码的算术移位就是 符号位保持不变, 仅对数值位进行移动 .

进一步的讲:

原码右移 : 高位补0, 低位舍弃
原码左移 : 低位补0, 高位舍弃

注意: 右移的精度丢失 / 左移的数据溢出问题
刚刚的例子我们舍弃了一个0, 所以是没问题的.
我们如果再右移两位会发生什么? 会舍弃一个1, 得到一个结果2 .
这时, 我们如果再单看这个移位的效果, 就不是简单的 $ \div 2^1 $ 了, 它会自动舍弃掉丢失的那个小数 .
类似的, 我们左移的时候也会遇到数据溢出的问题, 这里也不再赘述.

再来看反码, 我们之前说过的, 正数反码就是原码, 负数反码是原码的 符号位不变, 数值位取反 .

因此对于反码:

正数反码 : 移位规则同原码
负数反码 :
- 右移: 高位补1, 低位舍弃
- 左移: 低位补1, 高位舍弃

最后看补码, 正数补码还是原码, 负数补码是 反码+1 .

这意味着啥呢? 我们举个例子:

$$
\begin{align*}
& 原数值: & -20D \\
& 原码: & 1,0010100 \\
& 反码: & 1,1101011 \\
& 补码: & 1,1101100
\end{align*}
$$

这是啥意思呢, 负数补码数值位的 后半部分与原码一样, 前半部分与反码一样 , 所以方法就呼之欲出了:

注意: 后半部分
这个后半部分指的是 知道从后往前数第一个1为止 .

正数补码 : 移位规则同原码
负数补码 :
- 右移: 高位补1, 低位舍弃( 同反码 )
- 左移: 低位补0, 高位舍弃( 同原码 )

2.2.2.2 逻辑移位

逻辑移位更算术移位的区别在于, 逻辑移位是要带着符号位一块移的 .

注意: 逻辑移位的适用范围
一看这个移位的规则, 肯定不能用在有符号数上, ~~那一通移动那不乱套了~~ , 因此逻辑移位 一般只适用于无符号数 .

2.2.2.3 循环移位

循环移位的方式不太一样, 但规则比较简单.

我们要把 移出的那一位放在要补位的那一位上 .

而这种情况还有两种方式:

带进位位 : 移出的位放在进位位上, 进位位放在补位的位上
无进位位 : 直接把移出的位放在补位的位上

2.2.3 加减运算

聊完移位的, 再来聊聊加减. 首先我们要明确 加减通常不涉及到反码, 我们这里只探讨原码和补码 .

2.2.3.1 定点数的加减运算

我们先来探讨 原码的加减 , 之前我们提过原码正负相加的时候会出现的问题, 详见2.1.3

因此我们先把原码加减的三种情况捋出来:

正+正 : 数值位做加法, 结果为正
负+负 : 数值位做加法, 结果为负
正+负 : 数值位大-小, 符号同绝对值大的数

注意: 原码减法的处理方式
减法就将被减数换符号, 随后按照加法的方式运作即可.

当然, 我们这里也只是探讨一下这种情况, 这玩意在计算机里太难实现了. ~~用补码就可以仅用加法实现的东西, 为啥要节外生枝?~~

这之后, 我们看一下计算机中最通用的 补码的加减 .

在进行补码的加减运算时, 不需要考虑符号位, 只需要将对应的数值转变为补码后一同运算即可. 但问题来了, 我们看下面这么个情况:

$$
\begin{align*}
& A=15, C=124 \\
& [A]_补 = 0,0001111 , [C]_补 = 0,1111100 \\
& [A+C]_补 = 1,0001011 \space (对应真值-117)
\end{align*}
$$

我们看到, 上述情况中, 两个正数的补码相加最终得到了一个负数的补码结果, 这即我们所说的溢出 . 由于八位补码所能表示的数值范围为: $ 2^{-7} \leq x \leq 2^7-1 $ , 这已经无法表示原先的正数结果了.

因此, 我们得节外生枝, 说一说这个 溢出判断 该怎么实现.

我们首先得明确, 溢出这个事出现的情况:

正+正 , 结果为负
负+负 , 结果为正

因此, 我们给出几种判断溢出的逻辑:

(1)采用一位符号位时, 单独设置溢出判断位V

$$
\begin{align*}
& 加数A, 被加数B, 结果S \\
& 对应符号位: A_s, B_s, S_s \\
& V = \overline{A_s} \overline{B_s} S_s + A_sB_s \overline{S_s}
\end{align*}
$$

这个式子的意思即: 当加数与被加数符号相同, 并且结果符号与加数 / 被加数符号相反时, 则产生了溢出 .

(2)根据符号位的进位和最高数值位的进位情况判断溢出

符号位进位 $ C_s $

最高数值位进位 $ C_1 $

$$
\begin{array}{}
C_s & C_1 & Res \\
0 & 1 & 上溢 \\
1 & 0 & 下溢
\end{array}
$$

又或者当不需要判断上溢还是下溢的时候, 只需要判断:

$$ V = C_s \oplus C_1 $$

即可.

注意: 标志位OF的产生方式
请读者回看2.2.1.1中加法器的溢出标志位OF的逻辑表达式, 其使用的溢出判断方式即如上所述.

(3)采用双符号位的补码来表示数值

$$
\begin{array}{}
& 加数 & 00,0001111 \\
& 被加数 & 00,1111100 \\
& Res & 01,0001011
\end{array}
$$

可见当最终结果两个符号位不同时, 代表出现了溢出. 其中, 前侧的符号位代表结果原本的符号位 .

注意: 双符号位补码的存储方式
双符号位补码在计算机中同样 只存储一个符号位 , 只不过在运算时会复制一个符号位而已.

2.2.3.2 无符号数的加减运算

唠完有符号数, 无符号数就显得友好许多. 这玩意没有符号的限制, 直接加就完了.
但是到了减法这一块, 问题出现了: 无符号数没有补码, 怎么整?

要解决这个问题, 我们需要回忆一下补码的含义: 说白了就是一个数的补数 (详见2.1.3).
$ A-B = A+[B]_补 $
明确了这一点之后, 我们的问题就转变为: 怎么求减数的补数?

事实上, 无符号数的补数的求法与补码的求法几乎一致, 但不需要考虑符号位了(无符号数没有符号位).
全部位取反, 末位+1 即可.
这个事明白之后, 按照加法接着算就行了.

无符号数的加减怎么判断溢出?

加法: 最高位进位为 1 时发生溢出
减法: 最高位进位为 0 时发生溢出

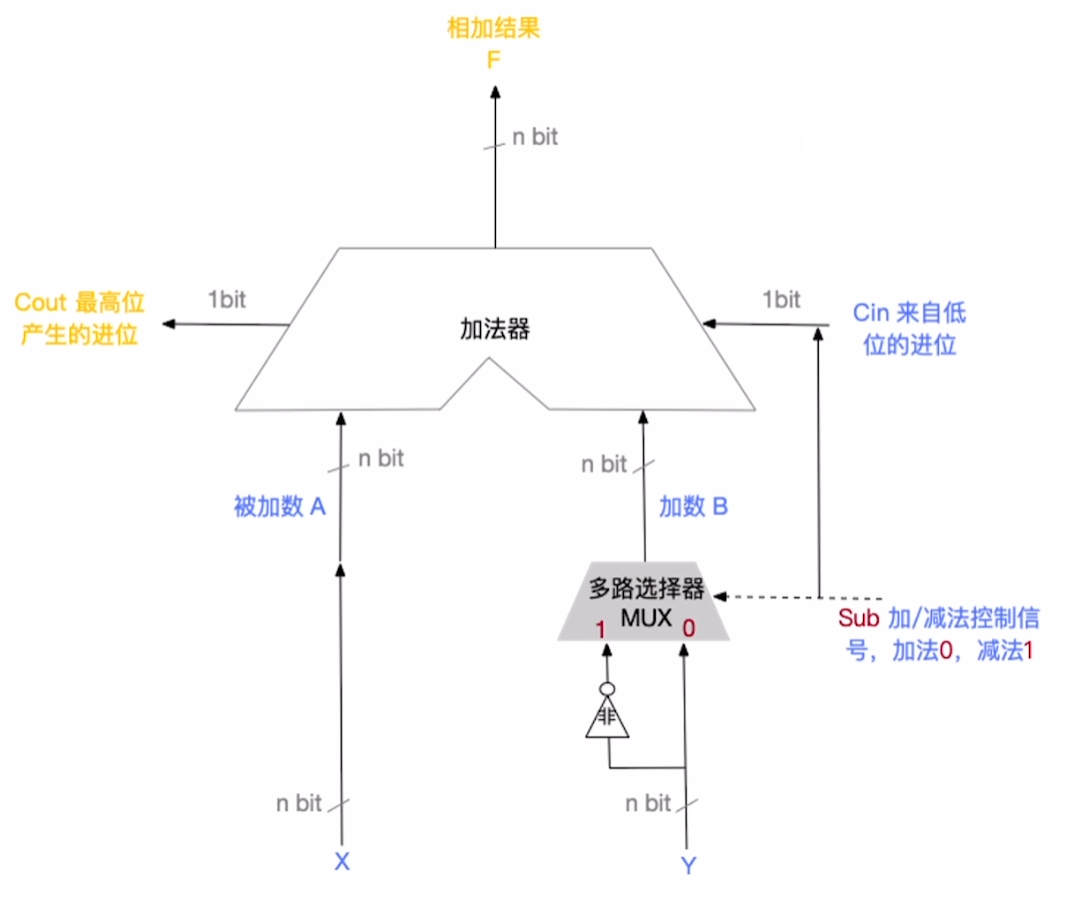
2.2.3.3 补码加减运算电路

我们看到右侧的 加减法控制信号Sub 同时连接到了加法器的 低位进位Cin 上, 回忆一下刚刚所提到了减法运算方式, 在传来减法后, 需要对减数所有位取反再+1变为加法. 这个电路设计就能实现这种运算方式.

注意: 标志位CF的产生方式
请读者回看2.2.1.1中加法器的无符号溢出标志位CF的产生方式. $ C_{in} \oplus C_{out} $
现在想一想为啥这个产生方式能够这样写出?
当 $ C_{in} = 0 $ 时, 代表当前为加法, 而无符号数加法的溢出标志为 最高位进位为1 ;
当 $ C_{in} = 1 $ 时, 代表当前为减法, 而无符号数减法的溢出标志为 最高位进位为0 ;
是不是刚好符合我们的电路设计 : )

2.2.4 乘除运算

基础的加减说完了, 现在说点更难的乘除. 同样的, 乘除也不会涉及到反码, 我们这里仅对原码和补码进行说明.

2.2.4.1 原码的乘法运算

我们首先得考虑一下乘法该怎么算, 列个 乘法竖式 .

那放到二进制里, 是不是一个道理?

这之后, 我们考虑一下竖式到底为什么要 错位相加 ?

按照之前提过的位权来思考这个问题:

$$
\begin{align*}
& 0.1011 = 1 \times 2^{-1} + 0 \times 2^{-2} + 1 \times 2^{-3} + 1 \times 2^{-4} \\
& 0.1101 = 1101 \times 2^{-4} \\
& 0.1011 \times 0.1101 = (1 \times 1101 \times 2^{-8}) + (1 \times 1101 \times 2^{-6}) + (1 \times 1101 \times 2^{-5})
\end{align*}
$$

可以看到, 随着位权递增, 对应到竖式里面就是错位相加了.

基本原理搞明白了, 到机器上还有些问题要考虑:

数字有正负, 符号位咋办?
乘积的位数太多了, 咋处理?
每一次的乘积都要保存下来最后统一相加吗? ~~当然不可能, 那64位的俩数相乘岂不是要有64个寄存器~~

第一个问题的解决方式很简单, 同原码加法一样, 符号位单独处理 .

$$ 符号位 = x_s \oplus y_s $$

注意: 这里异或的含义
代表着只有两数符号位不同(一正一负)时, 才会得到1(负数).

第二个和第三个问题, 我们就要看在机器中乘法的实现方式了.

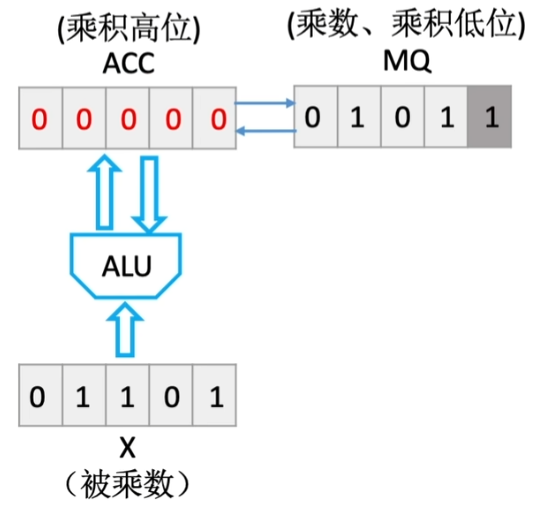
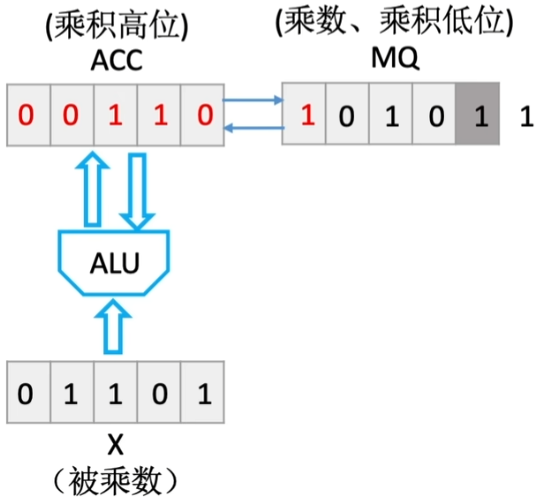
再放一遍这个图:

在乘法中, 三个寄存器各有作用:

ACC: 存放 乘积高位
MQ: 存放 乘积低位和乘数
X: 存放 被乘数

概念: 原码一位乘
指基于原码的, 每次仅逻辑右移一位的乘法形式.
下述过程即原码一位乘的具体说明.

我们以如下的例子做一个说明:

$ x_原 = 1.1101, y_原 = 0.1011 $

(1)符号位单独运算, 得到结果的符号位, 此例中为1

(2)将ACC置零; 并将被乘数和乘数分别放入X和MQ中

注意: MQ最低位
上图中MQ最低位进行了加深标记, 代表着该位是参与下一次乘法的位.

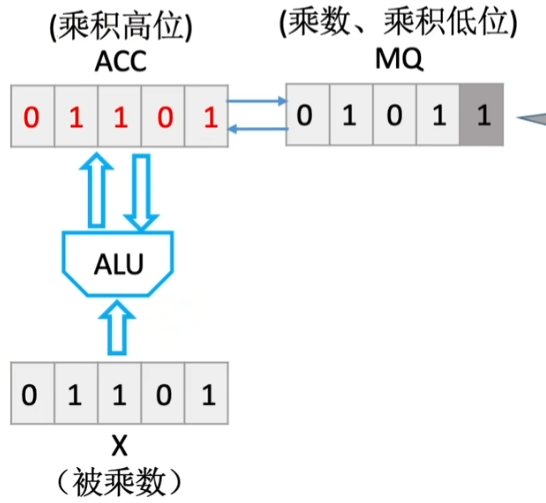
(3)观察当前MQ最低位, 是1则令ACC加上被乘数, 是0则令ACC加0(加法通过ALU实现)

(4)ACC与MQ统一逻辑右移一位

注意: MQ中原先的最低位被抛弃
因为原先MQ最低位的位权加和已经完毕, 因此此处可以直接将其丢弃. 将位置腾出来用于存放乘积的低位.

概念: 部分积
指计算机乘法运算中, ACC与MQ中用于存储乘积的部分.
就是上图中红色数字的部分.

(5)从(3)开始重复上述步骤n次(n为数值位个数), 直至乘数的数值位完全移出MQ为止

(6)增添上(1)中计算得到的符号位即可

最终我们可以得到正确的结果, 其小数点隐含在符号位后方.

注意: 整数乘法
与小数乘法原理相同, 将小数点变更为分隔符号位的逗号即可.

在王道Bilibili的计算机组成原理课程中, 并未提及 原码两位乘 的移位和加减方式, 在本文中进行额外补充.

概念: 原码二位乘
指基于原码的, 每次仅逻辑右移两位的乘法形式.

原码二位乘的主要目的在于 提高计算机的运算效率 , 其计算原理跟一位乘很类似.

既然名为 二位乘 , 自然意味着我们 一次加法需要利用到MQ的后两位 , 并在进行对应处理后 逻辑右移两位 .
我们先给出运算中乘积高位与被乘数的加法准则, 随后再对这个准则进行解释.

$$
\begin{array}{}
& y_{i-1} \space y_i & C_j & 操作内容 \\
& 0 \space 0 & 0 & 原部分积右移两位, C_j = 0 \\
& 0 \space 0 & 1 & 原部分积+X, 右移两位, C_j = 0 \\
& 0 \space 1 & 0 & 原部分积+X, 右移两位, C_j = 0 \\
& 0 \space 1 & 1 & 原部分积+2X, 右移两位, C_j = 0 \\
& 1 \space 0 & 0 & 原部分积+2X, 右移两位, C_j = 0 \\
& 1 \space 0 & 1 & 原部分积-X, 右移两位, C_j = 1 \\
& 1 \space 1 & 0 & 原部分积-X, 右移两位, C_j = 1 \\
& 1 \space 1 & 1 & 原部分积右移两位, C_j = 1 \\
\end{array}
$$

对上表进行一个解释:

$ y_{i-1} / y_i $ : 指的是MQ的最低两位.
$ C_j $ : 指的是一个单独的标志位, 用于标记上一次运算时是否有欠账

注意: 欠账?
$ y_{i-1} / y_i $ 总共有四种可能: 00 / 01 / 10 / 11, 对应着要加 0 / 1 / 2 / 3 个被乘数X.
加 0 / 1 / 2 个被乘数都比较简单, 可以直接通过将被乘数逻辑左移来实现(左移一次相当于乘2), 唯独这个 加3个X 比较难搞.
因此为了加速运行, 将 加3个X 拆开来, 变成 加4个X再减1个X .
加4个X 可以直接在 部分积右移两位后加1个X , 而 减1个X 则在当次计算中进行完毕.
因此这个 $ C_j $ 就代表着一个欠账的含义, $ C_j = 1 $ 代表着需要在右移后多补上一个X.

2.2.4.2 补码的乘法运算

补码的乘法运算涉及到一个新算法 Booth算法 .
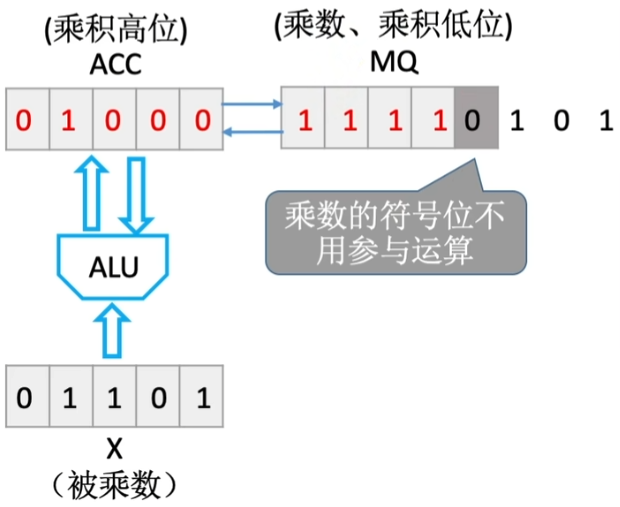
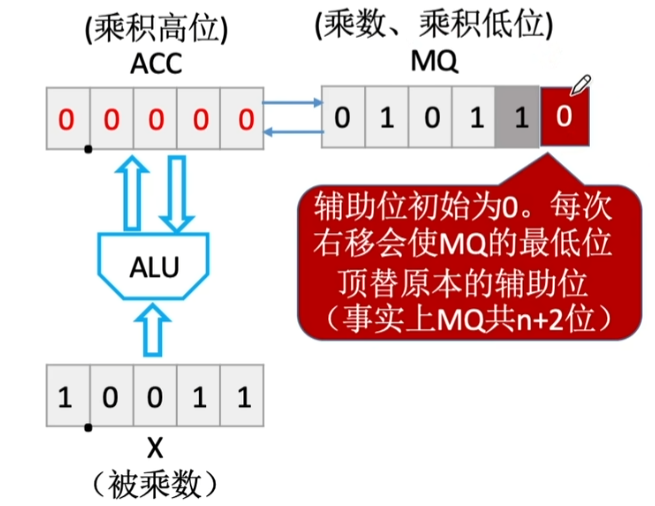
这个方法的特点在于 符号位也参与运算 . 此外, MQ寄存器多出一个 辅助位 进行单独的运算辅助; 对应的ACC与X寄存器也要多一位, 一般此时利用 双符号位数据 来填充这多出来的一位.

注意: MQ辅助位的位置
实际上, Booth中添加的辅助位就是原先一位乘中每次丢失的那一个乘数.

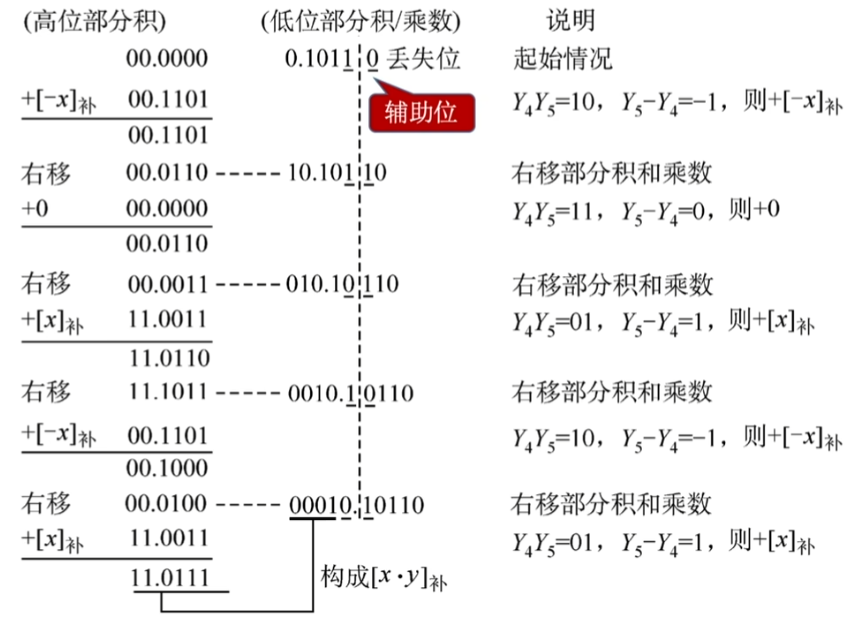
在Booth中, 可能加上的数值有以下三种可能:

$$
\begin{array}{}
& 原MQ最低位y_i & 辅助位y_{i+1} & 操作内容 \\
& 0 & 0 & 部分积+[X]_补, 算数右移一位 \\
& 0 & 1 & 部分积+0, 算数右移一位 \\
& 1 & 0 & 部分积+[-X]_补, 算数右移一位 \\
& 1 & 1 & 部分积+0, 算数右移一位
\end{array}
$$

注意: 部分积算数右移时的补位原则
这里使用的是 补码运算 , 因此请格外注意部分积右移时该怎么补空缺出来的位.
具体而言, 补与 当前符号位 相同的数即可.

与原码相比, 补码的乘法由于 符号位也参与运算 , 最后会要 额外进行一次加法 , 但最后一次加法过后 无需右移 .

2.2.4.3 原码的除法运算

说完了乘, 我们来看看除.
还是要从最开始的那个问题谈起, 我们最开始是怎么做除法的?

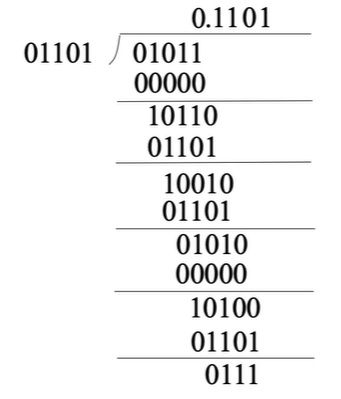
我们此前学过的除法是这么算的, 每一次都尽可能让除数接近上一次求出的余数, 随后得出新一轮的余数.
能不能类比到二进制上?

一个道理, 对吧, 甚至二进制的位数判断要更简单一些, 只需要判断当前位的结果是0还是1即可.

好的, 现在问题简单了~~(简单个锤子)~~ , 怎么把这种手算的思想转化为计算机的形式?

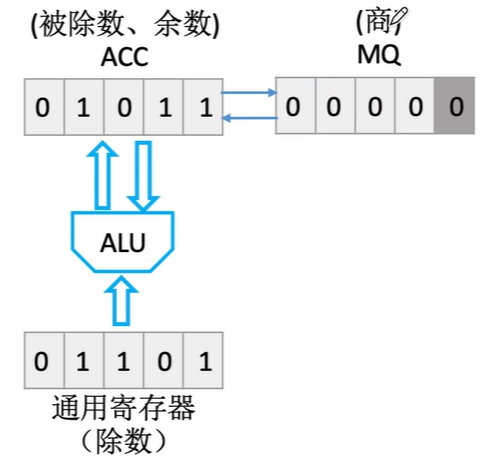
我们还得放一遍这个图:

除法中, 三个寄存器同样各有作用:

ACC: 放置 被除数和余数
MQ: 放置商
X: 放置除数

下面我们给出第一种进行原码除法的方法: 恢复余数法

(1)确定结果符号, $ Res_s = x_s \oplus y_s $

(2)取被除数x, 除数y的绝对值进行计算, 分别写出: $ [x]_原, [y]_原, [y]_补, [-y]_补 $

(3)将 $ [x]_原 $ 放入ACC, $ [y]_原 $ 放入X, MQ置零

注意: MQ的最低位
这里MQ的最低位就是我们要确定的一位商, 将其标注为了深灰色.

(4)计算机默认将MQ的最低位置1, 随后进行如下操作: $ (ACC) = (ACC) - (X) $ , 即将ACC内的值减去除数, 再次放入ACC

注意: $ [-y]_补 $ 的作用
经过前面对于减法的学习, 我们知道实际上减法就是加上对方相反数的补码, 因此这一步用到了我们(2)中写到的 $ [-y]_补 $

(5)检测当前ACC中的符号位, 如果为0则进入下一步, 如果为1则再进行 $ (ACC) = (ACC) + (X) $ , 即将ACC内的值加上除数, 再次放入ACC, 并将MQ的最后一位改为0, 进入下一步

注意: (4)(5)之间的关系
(4)的实际意义是: 计算机先假设这一位商是1, 然后计算出商为1时的结果.
(5)的意义在于判断(4)的假设是否正确, 如果ACC此时是正数, 代表这一位商就应该是1, 无需更改; 如果ACC此时是负数, 代表这一位商不应当是1, 因此需要将刚刚减去的除数加回来, 并将错误的商1改回商0.

(6)ACC与MQ一同逻辑左移一位, 并重复(4)-(5)的过程, 直到MQ被占满(即商的长度已经达到机器字长的情况)后, 停止过程.

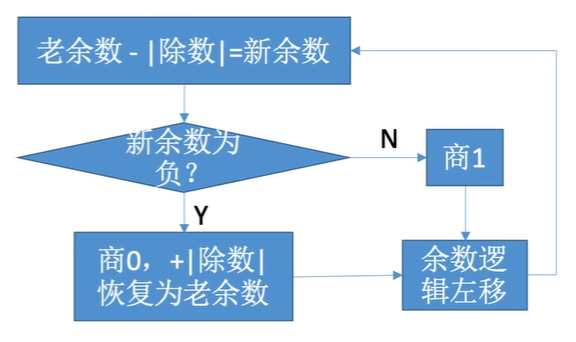
给出全过程的流程图:

上面这方法已经挺好, 但我们还是想再往前走走, 因为这方法判断完还要恢复余数, 太费劲了.
要优化, 我们要考虑每次恢复余数之后我们干了点啥:

我们记当次被除数减去除数后的得到的数值为 $ a $ , 除数为 $ b $ .

$$
\begin{align}
& if(a<0) & \tag 0 \\
& (ACC) = (a+b) & 恢复余数 \tag 1 \\
& (ACC) = 2(a+b)=2a+2b & 逻辑左移 \tag 2 \\
& (ACC) = 2(a+b)-b = 2a+b & 再次减去余数 \tag3 \\
& else \space if(a>0) & \tag 0 \\
& (ACC) = 2a & 逻辑左移 \tag 1 \\
& (ACC) = 2a-b & 再次减去余数 \tag2
\end{align}
$$

因此我们可以直接跳过 恢复余数 这个过程, 根据减去余数的正负直接确定下一次减去余数的数值.
具体而言:

$ a>0 $ : 左移, 减除数
$ a<0 $ : 左移, 加除数

这种方法被我们称之为 加减交替法 .

注意: 加减交替法的最后一步
最后一步因为要得出最终结果了, 因此余数的符号位应当保证与被除数的符号位相同, 因此此时还是要恢复余数的.

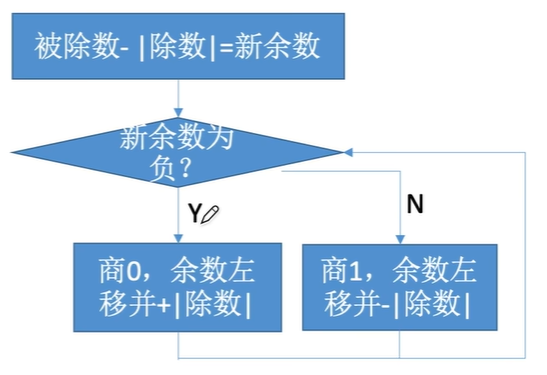
我们给出加减交替法的流程图:

原本而言, 这里应该是有一个补码的除法的, 但是实话实说的讲, 补码除法这里笔者也没看明白, 所以不误导人了, 请有兴趣的读者自行寻找相关资料吧 : (

2.3 浮点数及其相关运算

好的, 定点数这一大关, 我们好说歹说算是过去了~~(稀里糊涂的?)~~

接下来我们得来看看另一类费劲的玩意, 叫 浮点数 .

2.3.1 浮点数的表示

首先聊聊为啥非得整个浮点数? 当然是我们之前整的定点数有缺陷.
非常典型的案例即定点数的 数据表示范围被卡的很死 , 它与数据长度息息相关, 但无限制的扩充数据长度又是不现实的.

我们此前在十进制中怎么表示很大的数呢? 科学计数法 , 对吧.
因此我们仿照着科学计数法的思路, 来考虑一下浮点数的设计方式:

$ 3.026 \times 10^{11} $ , 这是个用科学计数法表示的很大的数. 我们要记录的有两个部分:

阶码 : 即上述案例中的 $ +11 $
- 阶符 : 阶码的符号
- 阶码的数值
尾数 : 即上述案例中的 $ 3.026 $
- 数符 : 尾数的符号
- 尾数的数值部分

我们按照科学计数法的方式来理解, 可以得到这么个结论:

阶码控制数据可表示的大小, 尾数控制数据可表示的精度 .

在计算机中, 阶码常常是用 移码或补码 表示的定点整数; 尾数常常是用 原码或补码 表示的定点小数.

因此, 我们给出浮点数的定义:

$$ N = r^E \times M $$

r: 阶码的底, 通常为2
E: 阶码
M: 尾数

寻思完了浮点数的定义, 来聊一个标准化的问题, 在本处被称为 浮点数的规格化 .

我们知道同一个真值, 其浮点数是可以通过多种方式来表示的:

例子
给出两个二进制的浮点数:
$ 0,11;0.0101 $
$ 0,10;0.1010 $
这俩数是不是一样?

我们一寻思, 下面那个数应该更好一点, 因为其表示的尾数精度要更高一些对吧.
因此我们给出规定, 尾数数值位 的最高一位应当是一个 有效值 , 这样的浮点数被称为 规格化的浮点数 .

而我们上面那个例子中, 将第一个浮点数转变为第二个浮点数的过程, 相当于将尾数左移了一位 , 因此这种情况我们称为左规 .

概念: 左规 / 右规
左规: 指将尾数进行 算数左移 , 阶码减一 .(通常用于运算后结果尾数最高位不是有效值时)
右规: 指将尾数进行 算数右移 , 阶码加一 .(通常用于运算后结果尾数符号位不同时, 意味着产生了溢出, 这种情况下一般采取多符号位)

好的, 我们随后说说 规格化数的特点 :

原码表示的尾数 : 最高位为1
- 正数
  - 最大值: $ 0.11…1 $
  - 最小值: $ 0.10…0 $
  - 表示范围: $ \frac{1}{2} \leq x \leq (1-2^{-n}) $ , n为 尾数的数值位的位数
- 负数
  - 最大值: $ 1.10…0 $
  - 最小值: $ 1.11…1 $
  - 表示范围: $ -(1-2^{-n}) \leq x \leq - \frac{1}{2} $
补码表示的尾数
- 正数: 同原码, 最高位为1
  - 最大值: $ 0.11…1 $
  - 最小值: $ 0.10…0 $
  - 表示范围: $ \frac{1}{2} \leq x \leq (1-2^{-n}) $
- 负数: 由于我们此前提过的, 补码数值位的前半部分同反码, 因此最高位为0
  - 最大值: $ 1.01…1 $
  - 最小值: $ 1.00…0 $ 注意这里就是-1的补码
  - 表示范围: $ -1 \leq x \leq -(\frac{1}{2} + 2^{-n}) $

规格化之后, 我们要继续往后说以下 浮点数的溢出 .
因为即使是浮点数, 也有表示不了的范围不是?

这个情况下我们需要一并考虑阶码和尾数, 刚刚已经把尾数的范围表示完了, 那阶码就相当于在尾数的范围上乘上一个对应的权值对不?

例子
假设阶码共3位(意味着阶码的数值位只有2位, 阶码的数值范围为 $ -4 \leq x \leq 4 $ ), 以原码表示尾数:
该浮点数的正数表示范围区间:
$ \frac{1}{2} \times 2^{-4} \leq x \leq (1-2^{-n}) \times 2^4 $
该浮点数的负数表示范围区间:
$ -(1-2^{-n}) \times 2^4 \leq x \leq - \frac{1}{2} \times 2^{-4} $

我们可以发现, 无论怎样, 浮点数总会在两个部分有表示不了的数字:

0的左右
能表示的上限值的右侧, 下限值的左侧

因此, 我们给这几个部分的溢出分别取了几个名字:

注意: 溢出的解决方案
通常, 下溢会被我们直接当作0处理, 而上溢则会抛出对应异常.

注意: IEEE754 内容缺失
IEEE 754是当前公认的对浮点数的计算机内存储方式, 但奈何博主实在是没捯饬明白这一部分的内容, 只得有待将来补充了. 读者见谅.

2.3.2 浮点数的加减运算

好了, 我们进入浮点数的运算部分, 从加减开始.

我们先明确运算的步骤:

对阶
- 将阶数表达为同一个值. 如 $ 1.2 \times 10^{10} + 1.2 \times 10^{12} $ , 那肯定是先把这俩数后面的乘阶改成一样大的之后才能算是不是.
- 通常原则是 小阶向大阶看齐 .
尾数加减
- 按照此前讲述的定点数加减法进行即可.
规格化
- 按照此前讲述的浮点数规格化的原则进行即可.
舍入
- 浮点数尾数的位数是有限的, 但在对阶的过程中会出现小数过长的情况(因为变小了嘛). 因此可能会出现需要舍弃结果中的某些低位部分的情况, 这时候要决定是否要向对应的高位进1.
判断溢出
- 即某些情况下, 阶码的大小已经超出了浮点数阶码能够表示的范围(比如位数太多了), 此时要进行溢出处理.

注意: 小阶向大阶看齐?
读者不妨想一想如果反过来, 让大阶向小阶看齐会发生什么?
那上面的例子中, $ 1.2 \times 10^{12} $ 就会变成 $ 120.0 \times 10^{10} $
这种数的问题是小数点前面的有效位太多了, 计算机挺不好处理的, 按照此前我们商定的原则, 尾数转换时只会变小, 不会变大. 更便于计算机处理.

由于这里大部分是之前涉及到的知识, 就不给太详细的说明了, 给出一个王道考研课中的样例供读者参考.