密码学 Chap.4 分组密码
1. 概述
1.1 引入
分组密码 , 实质上描述的是一种加密方式, 它将明文分为一个个等长的消息组, 在密钥的控制下按固定算法分别进行每组的加密, 最终再将 等长的 密文组拼接后输出.
$$ m_1, m_2, …, m_k \to (m_1, m_2, …, m_n)(m_{n+1}, m_{n+2}, …, m_{2n})… \to (y_1, y_2, …, y_m)(y_{m+1}, y_{m+2}, …, y_{2m})… $$
1.2 基本概念
- n / m : 分组长度. 我们可见, 分组密码的分组长度与加密后的分组长度不一定相同.
- n > m 时, 称为有数据压缩的分组密码.
- n < m 时, 称为有数据扩展的分组密码.
- n = m 是最常见的方式.
- 实质上, 研究分组密码就是研究 $ (x_1,x_2, …, x_n) \to (y_1, y_2, …, y_m) $ 这一过程.
可见, 通常而言研究的就是明 / 密文的二元组, 因此也可表示为 $ GF(2)^n \to GF(2)^m $ 的映射.
1.3 历史沿途
这一部分简单了解即可.
分组密码出现的标志是上世纪70年代出现的 美国数据加密标准 DES (Data Encryption Standard) 算法 . 它所持有的一些特征也为当代的分组密码所继承, 如算法完全公开, 信息安全性大程度取决于密钥的安全性等.
1.4 关于安全性
分组密码作为不同于古典密码的新产物, 其出现目的在于防范来自于现代计算机的攻击, 因此其安全性标准要更复杂一些.
现代分组密码的 密码算法是完全公开的 , 这意味着其安全性仅依赖于密钥的复杂程度.
评判分组密码的安全性, 首先需要考虑攻击者可能获取到什么信息:
- 截获在不安全信道上传输的全部密文
- 攻击者的计算能力
- 获得的其余信息等
在攻击者拥有的信息越多 / 拥有的计算能力越强的前提下, 如果一个系统仍然是安全的, 则这个系统的安全性越高.
所谓 相对安全 与 绝对安全 的概念也源于这个考量, 当一个系统对于一个拥有无限计算机资源的攻击者都是安全的, 则这个系统被称之为绝对安全的系统. 反之则均称之为相对安全的系统.
很遗憾, 当前来看, 绝对安全的系统并不存在. 因此我们通常从密码应用时期的硬件算力所需的破译时间来进行评判一个相对安全的系统.
如果攻击者利用其手中有限的算力破译该密码算法所需要的时间远超该新系统所保护的内容的有效期,我们称这个系统是 计算上安全的
1.5 分组密码的设计原则
人们认为分组密码应当具备两个特性:
- 复杂-难于分析
- 分组长度足够大
- 密钥量足够大
- 混乱和扩散 :
- 混乱: 指的是使得明文和密文之间的统计特性难以分析
- 扩散: 指的是每一位明文数字的影响都应当迅速地体现在密文多个输出的数字中
- 简单-易于实现
- 硬件实现则必须高效
- 软件实现则必须灵活 / 代价低
混乱(Confusion) 与 扩散(Diffusion) 是由香农(Shannon)提出的两个一般性的现代密码设计原则
复杂与简单 这两个要求其实有着本质性的矛盾, 分组密码的目的在于设计出能在二者之间找到平衡的算法.
2. 迭代密码
2.1 迭代?
如上文所说, 为了在复杂与简单之间找到平衡, 提出了 迭代密码 这一创新性的概念, 它意味着将一个简单的密码算法进行多轮循环迭代, 从而达到复杂的效果.
我们给一个具体定义:
定义 $ K $ 为一个确定长度的二元密钥, 迭代算法会指定一个固定的 / 公开的密钥编排方案, 得到 $ N_r $ 个 轮密钥 (也称 子密钥 ) , 记为 $ (K_0, K_1, …, K_{N_r}) $ . 此后, 还会设计一个公开的 轮函数 $ g $ , 它以 轮密钥 $ K_r $ 以及当前状态 $ w_{r-1} $ 作为输入, 输出当前轮的中间状态 $ w_r $ .
轮函数即:
$$ w_r = g(K_r, w_{r-1}) $$
初态 $ w_0 $ 被我们定义为明文, 经过 $ N_r $ 轮的最终态 $ w_{N_r} $ 被我们定义为密文 $ y $ .
迭代密码的复杂性我们保证了, 但我们好像忘记了点问题, 咋解密?
对于迭代密码, 其解密的过程就是加密的逆过程, 因此, 除了上述定义外, 我们还要求轮函数 $ g $ 必须是可逆的 , 这使得解密者能够上述过程的逆过程重现明文.
2.2 Feistel 结构
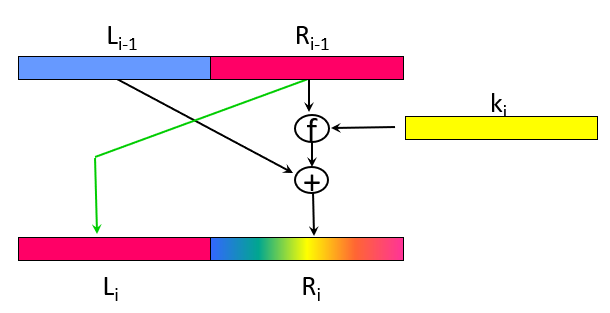
Feistel 结构是迭代密码的一种经典的具体实现, 它将每一个状态 $ w_r $ 分为左右两部分, $ L_i $ & $ R_i $ , 同时轮函数的输出也分为左右两部分, 其具体定义如下:
$$
\begin{aligned}
L_i & = R_{i-1} \
R_i & = L_{i-1} \oplus f(K_i, R_{i-1})
\end{aligned}
$$
这里的函数 $ f $ 是一个公开的函数, 它以轮密钥 $ K_i $ 以及当前状态 $ R_{i-1} $ 作为输入, 其输出与 $ L_{i-1} $ 进行异或运算后得出下一轮的 $ R_i $ .
3. DES
3.1 概述
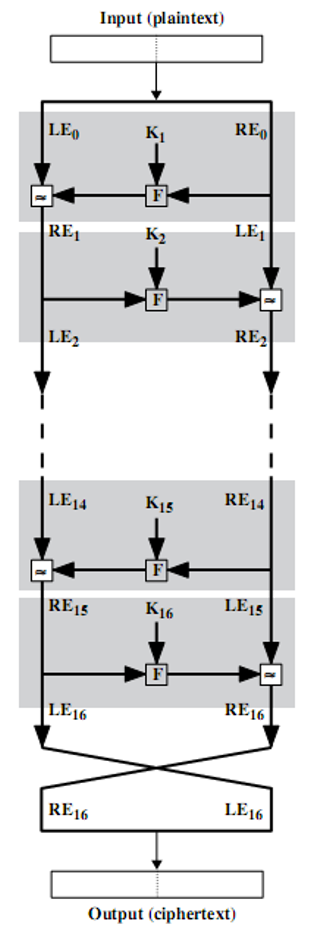
DES 是一种 16轮 的Feistel密码, 其分组长度为 64位 , 并用一个 64位 的密钥进行加密, 最终获取一个 64位 的密文串.
3.2 DES的具体流程
DES 的具体流程分以下几步:
- 初始置换 : 在对64位明文串进行加密前, 通常先对明文做一个初始的置换, 我们称之为 IP(Initial Permutation)
- 子密钥生成( Generate Subkeys ):
- 64位密钥初始置换, 我们称之为 PC-1(Permutation Choice 1) , 这个置换会将64位密钥变为56位密钥.
- 分为左右两部分 $ C_0 $ & $ D_0 $ , 每部分28位, 并对两部分分别根据当前轮数进行循环左移( Left Shift ).
- 左移后, 将两部分拼接起来, 得到56位的二进制串, 随后再进行一次置换 PC-2(Permutation Choice 2) , 这个置换进一步将56位二进制串变为48位二进制串(该串即为当轮子密钥).
- 将上述过程循环16次, 得到16个子密钥.
- 16轮迭代 :
- 根据Feistel结构, 将64位明文串分为左右两部分, 分别记为 $ L_0 $ & $ R_0 $ , 各32位
- 下一轮的左侧 $ L_i $ 就是上一轮的右侧 $ R_{i-1} $
- 下一轮的右侧 $ R_i $ 需要先计算 $ f $ 函数:
- 将 $ R_{i-1} $ 先进行一次扩展置换 E(Expansion Permutation) , 得到一个48位二进制串, 我们称之为 $ E(R_{i-1}) $
- 将这个 48位串 $ E(R_{i-1}) $ 与 当轮子密钥 $ K_i $ 进行异或运算, 得到一个48位二进制串, 我们称之为 $ S_2 $
- 将该48位串 $ S_2 $ 按照一定的规则分成8个6位串, 每个6位串通过一个S盒置换变为一个4位串, 最终得到一个32位二进制串, 我们称之为 $ S_3 $
- 最终将 $ S_3 $ 进行一个置换 P(Permutation) , 得到 $ f(R_{i-1}, K_i) $
- 下一轮的右侧 $ R_i $ 就是 $ L_{i-1} \oplus f(R_{i-1}, K_i) $
- 上述过程循环16次, 得到 $ L_{16} $ & $ R_{16} $
- 尾部逆置换 : 最后将 $ L_{16} $ & $ R_{16} $ 反向拼接起来, 再进行一个 逆置换(Inverse Permutation) , 得到最终的64位密文串.
3.3 具体说明1: 置换?
上述过程中多次涉及到了 置换 这一概念, 在DES中, 置换是通过矩阵体现的.
我们以初始置换为例:
const int IP[64] = {
58, 50, 42, 34, 26, 18, 10, 2,
60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6,
64, 56, 48, 40, 32, 24, 16, 8,
57, 49, 41, 33, 25, 17, 9, 1,
59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5,
63, 55, 47, 39, 31, 23, 15, 7
};我们进一步给出上述过程中用到的全部置换矩阵:
const int IP_INV[64] = {
40, 8, 48, 16, 56, 24, 64, 32,
39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30,
37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28,
35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26,
33, 1, 41, 9, 49, 17, 57, 25
};
const int EP[48] = {
32, 1, 2, 3, 4, 5,
4, 5, 6, 7, 8, 9,
8, 9, 10, 11, 12, 13,
12, 13, 14, 15, 16, 17,
16, 17, 18, 19, 20, 21,
20, 21, 22, 23, 24, 25,
24, 25, 26, 27, 28, 29,
28, 29, 30, 31, 32, 1
};
const int PC1[56] = {
57, 49, 41, 33, 25, 17, 9,
1, 58, 50, 42, 34, 26, 18,
10, 2, 59, 51, 43, 35, 27,
19, 11, 3, 60, 52, 44, 36,
63, 55, 47, 39, 31, 23, 15,
7, 62, 54, 46, 38, 30, 22,
14, 6, 61, 53, 45, 37, 29,
21, 13, 5, 28, 20, 12, 4
};
const int PC2[48] = {
14, 17, 11, 24, 1, 5,
3, 28, 15, 6, 21, 10,
23, 19, 12, 4, 26, 8,
16, 7, 27, 20, 13, 2,
41, 52, 31, 37, 47, 55,
30, 40, 51, 45, 33, 48,
44, 49, 39, 56, 34, 53,
46, 42, 50, 36, 29, 32
};
const int P[32] = {
16, 7, 20, 21, 29, 12, 28, 17,
1, 15, 23, 26, 5, 18, 31, 10,
2, 8, 24, 14, 32, 27, 3, 9,
19, 13, 30, 6, 22, 11, 4, 25
};上述矩阵的意义为, 原二进制串中的第 IP[i] 位, 将会移动到新二进制串的第 i 位. 比如原串中的第 58 位, 将会移动到新串的第 1 位.
DES中几乎全部的置换都是通过这种形式进行的, 并且每个置换对应的置换矩阵是固定的 / 公开的.
3.4 具体说明2: S盒?
在DES中, S盒是DES的另一个核心部分, 每一个S盒都将一个6位的二进制串转为4位, 共8个S盒, 它将48位二进制串变为32位二进制串.
我们以第一个 S盒 为例:
{
{14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7},
{ 0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8},
{ 4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0},
{15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13}
}该盒中有4行 / 16列, 我们假设待转的6位串为 110101 :
- 将第一位与最后一位取出来, 拼接后作为行数: 即 11 , 第3行
- 将第二位至第五位取出, 作为列数: 即 1010 , 第10列
- 取出的数为 3 , 转化为对应的4位二进制串: 0011
剩余的S盒如法炮制即可.
const int Sbox[8][4][16] = {
{
{14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7},
{ 0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8},
{ 4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0},
{15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13}
},
{
{15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10},
{3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5},
{0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15},
{13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9}
},
{
{10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8},
{13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1},
{13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7},
{1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12}
},
{
{7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15},
{13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9},
{10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4},
{3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14}
},
{
{2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9},
{14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6},
{4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14},
{11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3}
},
{
{12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11},
{10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8},
{9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6},
{4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13}
},
{
{4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1},
{13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6},
{1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2},
{6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12}
},
{
{13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7},
{1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2},
{7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8},
{2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11}
}
};3.5 具体说明3: 生成子密钥时的左移?
生成子密钥的左移是 循环左移 , 每次左移的位数由轮数决定, 具体每轮左移位数由一个数组给出:
const int SHIFT_SCHEDULE[16] = {
1, 1, 2, 2, 2, 2, 2, 2,
1, 2, 2, 2, 2, 2, 2, 1
};3.6 代码
博主在这里就不给全部代码了, 将几个重要功能的代码给出: (生成子密钥 / F函数)
void generateSubKey(const bitset<64> key_bin, vector<bitset<48>>& subkey) {
//Generate sub-key
//PC1
bitset<56> permutedKey;
for (int i = 0; i < 56; i++) {
permutedKey[i] = key_bin[PC1[i] - 1];
}
//Left-shift
bitset<28> right(permutedKey.to_string().substr(0, 28));
bitset<28> left(permutedKey.to_string().substr(28, 56));
for (int i = 0; i < 16; i++) {
for (int j = 0; j < SHIFT_SCHEDULE[i]; j++) {
bool left_t = left[0];
bool right_t = right[0];
for (int k = 1; k < 28; k++) {
left[k - 1] = left[k];
right[k - 1] = right[k];
}
left[27] = left_t;
right[27] = right_t;
}
bitset<56> temp;
for (int j = 0; j < 28; j++) {
temp[j] = left[j];
temp[28 + j] = right[j];
}
//PC2
bitset<48> sub;
for (int j = 0; j < 48; j++) {
sub[j] = temp[PC2[j] - 1];
}
subkey[i] = sub;
}
return;
}
bitset<32> f(bitset<32> R, bitset<48> subKey) {
bitset<48> expandR;
for (int i = 0; i < 48; i++) {
expandR[i] = R[EP[i] - 1];
}
expandR ^= subKey;
bitset<32> output;
for (int i = 0; i < 8; i++) {
int row = expandR[i * 6] * 2 + expandR[i * 6 + 5];
int col = expandR[i * 6 + 1] * 8 + expandR[i * 6 + 2] * 4 + expandR[i * 6 + 3] * 2 + expandR[i * 6 + 4];
int val = Sbox[i][row][col];
bitset<4> v(val);
string t = v.to_string();
reverse(t.begin(), t.end());
bitset<4> v_rev(t);
for (int j = 0; j < 4; j++) {
output[i * 4 + j] = v_rev[j];
}
}
bitset<32> output_P;
for (int i = 0; i < 32; i++) {
output_P[i] = output[P[i] - 1];
}
return output_P;
}3.7 讨论
DES 是一个十分完善的加密算法了, 但仍然有较为明显的争论:
- $ f $ 函数(尤其是S盒) 的设计原理未知
- 密钥长度过短: DES的实际密钥只需要56位的枚举, 因此在当前算力的条件下, 其无法抵御穷举式攻击
随后, 为了解决上述问题, 也推出了二重DES / 三重DES算法.
4. 分组密码的工作模式
DES只负责对64位的密钥进行加密, 但实际生活中大部分明文是远超64位的, 因此我们设计了不同的工作模式, 使得DES可以处理任意长度的明文.
在1977年DES颁布后, 1981年针对该算法制定了4种基本工作模式, 随后在2000年又有一种工作模式被加入, 共计5种常用工作模式:
- ECB: Electronic Codebook
- CBC: Cipher Block Chaining
- CFB: Ciphertext Feedback
- OFB: Output Feedback
- CRT: Counter Mode
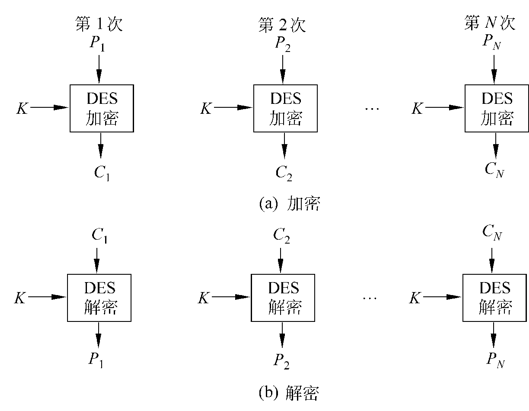
4.1 电子密码本(ECB)
电子密码本是最简单的工作模式, 其将明文分组后, 直接使用DES进行加密, 然后输出密文分组.
本模式中, 各分组的加密结果不受其余分组的影响.
ECB的优劣:
- 优
- 可并行处理
- 误差传递仅会出现在对应的一个分组上, 不会影响其他分组
- 劣
- 无法隐藏明文的模式信息(相同的明文加密出的一定是相同的密文)
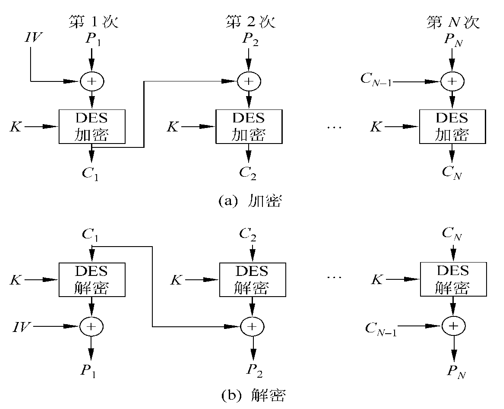
4.2 密文分组链接模式(CBC)
CBC模式在ECB的基础上, 引入了初始向量(IV), 使得每个分组在加密前, 都会与上一个分组的密文进行异或操作, 然后再进行加密.
各个分组的加密结果不仅受自身影响, 同时也受到其前方所有分组的影响( 这里有点类似区块链的感觉 )
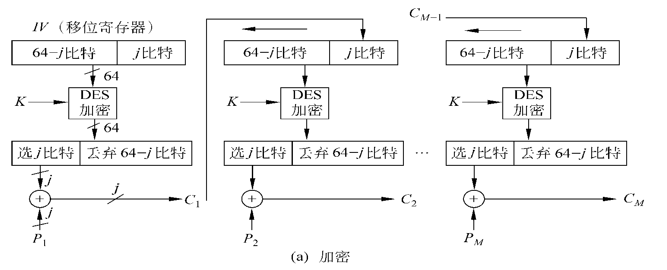
4.3 密文反馈模式(CFB)
CFB模式在CBC的基础上, 将加密过程拆分为两部分: 生成密钥流和异或操作.
CFB模式中, 每个分组在加密前, 都会先进行一次加密, 然后再与明文进行异或操作, 最后输出密文分组.
它相对于CBC好在哪? 我们会发现每一次加密过后, 会产生一定位数的 垃圾密钥流 , 因此如果出错, 其影响的位数是有限的, 因为迟早这种错误引发的影响会被新的密钥流覆盖掉.
至此, 本篇博文对于分组密码进行了初步梳理, 并给出了典型案例DES的详细实现.
本篇博文就到这里~