Chap.2 关系模型

我们在上一章(1.2.6)已经简要的给出的关系模型的大致概念, 本章中将对其进行进一步的讲解.

2.1 关系数据结构及形式化定义

2.1.1 关系

我们需要先给出关系的定义:

现实世界中的实体以及实体间的各种联系都可以用关系来表示, 从用户角度来看, 关系模型中数据的逻辑结构就是一张二维表.

给出一些关于关系的基本定义, 其实其中一部分在上一章的中提到过, 权当复习了:

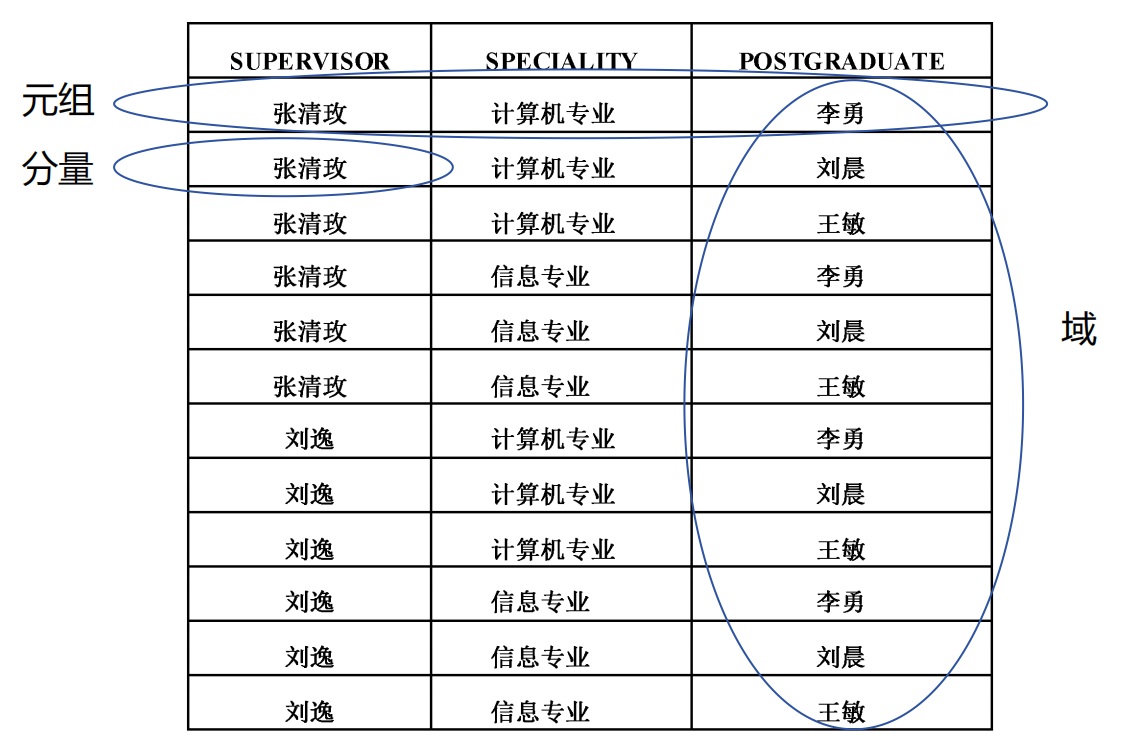
• 域(Domain): 一组具有相同数据类型的值的集合. 也就是我们说的某个属性的取值范围.
• 笛卡尔积(Cartesian Product): 是域上的一种集合运算.

给定一组域 $ D_1, D_2, …, D_n $ , 其笛卡尔积为:

$$ D_1 \times D_2 \times … \times D_n = \lbrace (d_1, d_2, …, d_n) | d_i \in D_i, i = 1, 2, …, n \rbrace $$

其实就是对于几个域中全部元素的全排列组合.

• 元组(Tuple): 在第一章中指的是一个表的某一行, 这里其实笛卡尔积的每一个元素都可以构成一个元组.
• 分量(Component): 在第一章中指的是某一行中的某个具体值, 在这里其实就是一个元组的某一个值 $ d_i $ .
• 基数(Cardinal number): 一个域允许的不同取值的个数(其实就是集合的元素数)
  • 考虑一个笛卡尔积的基数: $ M = \prod_{i = 1}^n m_i $

从这些定义可以看出来, 其实笛卡尔积可以用一张二维表表示, 表中每一行就是一个元组, 每列对应一个域, 每一格对应一个分量.

我们会发现笛卡尔积实际上会引出很多无意义的元组, 它们在现实中并不存在对吧.
因此, 我们可以把无意义的元组去掉, 得到一个关系的表.

我们引出关系的定义:

定义
关系 , 指的是一个笛卡尔积的子集.
$ D_1 \times D_2 \times … \times D_n $ 的子集叫做在域 $ D_1, D_2, …, D_n $ 上的关系. 表示为 $ R(D_1, D_2, …, D_n) $
R叫做关系名
n是关系的目(也叫关系的度)

对应的, 关系也有:

• 元组 : 关系中的每个元素
• n元关系 : 关系的度 = n
• 属性 : 关系中的每一列, n元关系必定有n个属性
• 码 : 能够 唯一标识 一个元组的一个 属性集
  • 这种属性集不一定只有一个, 因此每一个这种属性集都叫 候选码 .
  • 码不一定只有一个属性.
  • 码内的所有属性叫做 主属性 .
  • 不再码内的属性叫做 非主属性 .

注意
关系必须是有限集合.
实际上, 我们会给关系的每个属性附加一个名称(姓名, 学号, 年龄等), 这使得它们不再有顺序性.

• 主码(主键) : 就是我们选定的那个能唯一标识一个元组的属性集(从候选码中选出来的)
• 外码(外键) : 如果某个属性不是本关系的主码, 而是另一个关系的主码, 称之为本关系的外键.

这个外码有点难理解, 举个例子, 一个学生表中有一个属性叫 班级号 , 还有个表叫 班级表 .
这个班级号并不能唯一标识学生表, 但它是用来标明这个学生属于班级表中的哪个元组的, 这时候就叫它 外码(外键) .

我们根据上一章说的数据库的三个模式, 能想到其实有三类关系:

• 基本关系(基本表) : 就是实际存在的表(数据库的模式中的表)
• 查询表 : 查询结果对应的表(数据库的外模式中的表)
• 视图表 : 由基本表或者其它视图表导出的虚表(数据库的外模式中的表)

关系还有一种最重要的性质: 关系是不可再分的 .
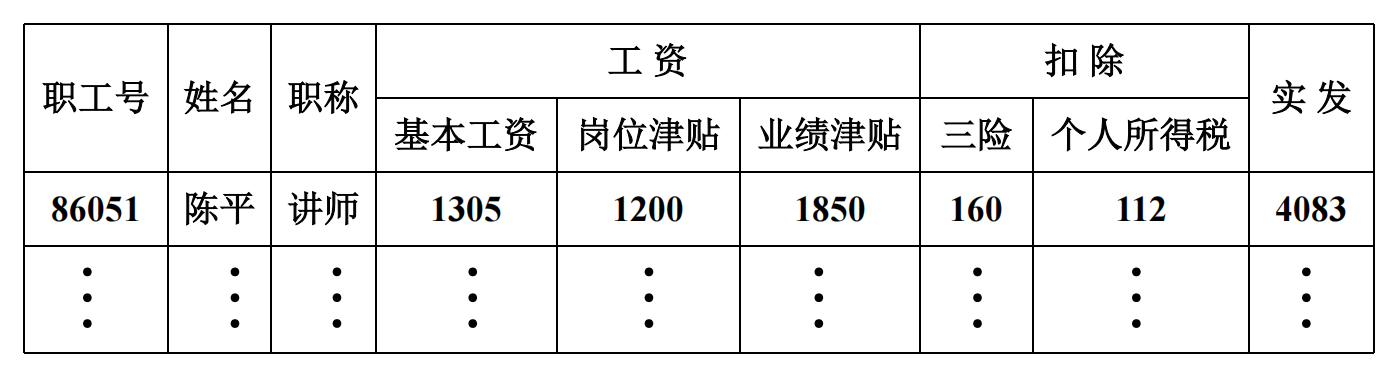
这是啥意思? 看这个例子:

在这个关系中, 工资 和 扣除 这两个属性是可以再分的. 这不符合关系模型的要求, 也可以叫做这个表 不规范化 .

那怎么规范化? 把工资和扣除单拆出去成两个表就可以了啊, 这个过程叫做 数据库的规范化 , 完全规范化的表叫做 范式(Normal Form, NF)

关于范式的概念我们之后还会再提, 读者在这里留个印象就好.

2.1.2 关系模式

2.1.2.1 关系模式的定义与形式化表述

关系模式的定义如下:

关系模式是对关系的描述, 包括元组集合的结构(属性构成, 属性域, 属性与域的映像关系)和完整性约束条件(实体完整性, 参照完整性, 用户定义的完整性)

读者如果对于目前讲的东西比较明白的话, 理解这个定义应该不太难.
给出关系模式的形式化表述:

$$ R(U, D, DOM, F) $$

• R: 关系名
• U: 组成该关系的属性名集合
• D: 该关系属性来自的域
• DOM: 属性向域的映射集合
• F: 属性间数据的依赖关系的集合(就是完整性约束)

这五个玩意里面读者不太明白的估计就是这个 DOM , 咋还出来个映射?

我们举个例子, 你有个学号, 它是个数字, U就是学号, D就是数字的取值, 但是你得单独定义一个映射, 告诉数据库, 我这个学号是个数字 .

这就是DOM, 它实际上是很多类似 $ 学号 \to INT $ 这样的映射关系.

2.1.2.2 关系模式的简单表述

上面这个形式化表述确实非常清晰, 但问题是, 写起来太麻烦了.
有些时候, 你只要写出属性名, 自然就知道这里面是个啥对不对.(比如你写个性别, 自然就知道里面只能出现男和女了, 别给我整武装直升机那一套奥 )

所以我们可以简单的把关系模式写成这样:

$$ R(U) = R(A_1, A_2, …, A_n) $$

其中 $ A_1, A_2, … $ 是一个个的属性名.

2.1.2.3 关系模式 Vs 关系?

这是两个比较相近的概念, 在这里还请读者加以区别.

关系 是动态的, 其内部是在不断发生变化的(一个表里面总会出现增删改查的行为对吧)
关系模式 是静态的, 它不会轻易变化, 就像一个大表里面不会轻易加某一列或者删除某一列一样.

2.1.3 关系数据库

关系数据库 就是支持关系模型的数据库.

其中, 对应关系模式的部分(就是定义结构的部分)叫 关系数据库的型 .
对应关系的部分(就是具体值)叫 关系数据库的值 .

2.1.4 关系模型的存储结构

这里我们简单了解即可, 因为数据库系统概论这门课程实际上不太关注内模式的具体实现.

通常有两种存储方式:

• 一个表对应一个文件, 将物理数据的组织交给操作系统
• 从操作系统那里申请若干个大文件, 自己划分文件空间, 自行组织

2.2 关系模型的完整性

我们之前说过关系的完整性:

• 实体完整性(主键唯一)
• 参照完整性(外键在对应的表内唯一)
• 用户定义的完整性(自主规定的约束)

这里给出三个完整性的具体定义:

2.2.1 实体完整性

若属性A是基本关系R的主属性 , 则属性A不能取空值.

典型例子就是你学号不能为空对吧.

2.2.2 参照完整性

参照完整性既然针对外键, 自然跟关系(或者直接说表)之间的引用有关. 其思路也完全符合逻辑: 不能引用不存在的实体.
定义如下:

若属性集K是R1的主码, 是R2的外码, 那么K在R2中要么为空, 要么是R1中的某个主码值

说白了, 你要么不引用, 要么就给我指到对的位置去, 你不能给我来个野指针这么个玩意.

我们举一个典型的多对多例子:

学生（ 学号 ，姓名，性别，专业号，年龄）
课程（ 课程号 ，课程名，学分）
选修（ 学号，课程号 ，成绩）

关于外键的补充说明:
如果关系 $ R_1 $ 中有一个关于关系 $ R_2 $ 的外键, 则:

• $ R_1 $ 叫: 参照关系
• $ R_2 $ 叫: 被参照关系

比如上例, 选修就是一个参照关系, 而学生和课程是两个被参照关系.

注意
参照关系和被参照关系可以是同一个关系! 同时参照关系中的外码也不一定要跟被参照关系中的主码同名!
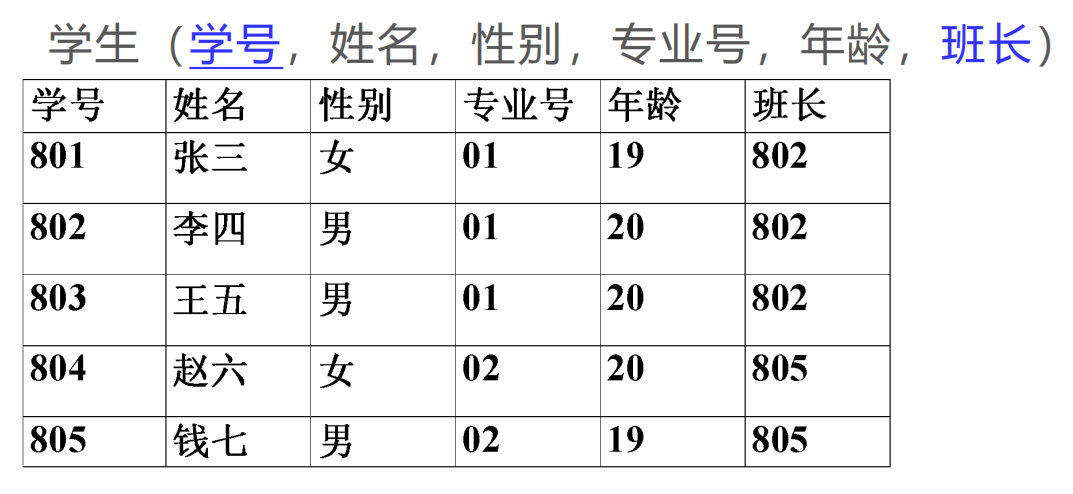
请看下例:

这个图中参照关系和被参照关系都是 学生 .
外码叫 班长 , 对应被参照关系中的主码叫 学号 .

2.2.3 用户定义的完整性

用户定义的完整性往往并不是必须项, 而是针对某一具体应用设计的必须满足的语义要求.

比如成绩一般必须大于0, 性别只能是男和女, 某一个非主属性也不能取空值等等.

2.3 关系操作

关系操作一般都被简要的称为增删改查, 但其实没那么简单:

• 查询操作:
  • 基本操作: 选择, 投影, 并, 差, 笛卡尔积
  • 导出操作: 连接, 除, 交
• 更新操作: 增删改

要进行相关的操作, 自然需要有相应的查询语言, 当前查询语言主要分两类:

• 关系代数语言(用集合运算表示)
• 关系演算语言(用谓词演算)

这一部分读者可以选择去看看离散数学. 当前主流的SQL语言具有两种语言的双重特点.

2.4 关系代数

我们这里只说关系代数, 关系演算就不提了, 毕竟, 关系是个集合.

关系涉及到的运算符有以下八种:

• $ \cup $ : 并
• $ - $ : 差
• $ \cap $ : 交
• $ \times $ : 笛卡尔积
• $ \sigma $ : 选择
• $ \pi $ : 投影
• $ \bowtie $ : 连接
• $ \div $ : 除

前四个我们挺熟悉, 后四个我们不太了解. ( 什么玩意 )

2.4.1 并 ( $ \cup $ )

要求是 关系R, 关系S 有相同的目(属性数) , 且相同的属性来自同一个域.
其实说白了, 两个表想合并, 是不是得有一样的属性啊.

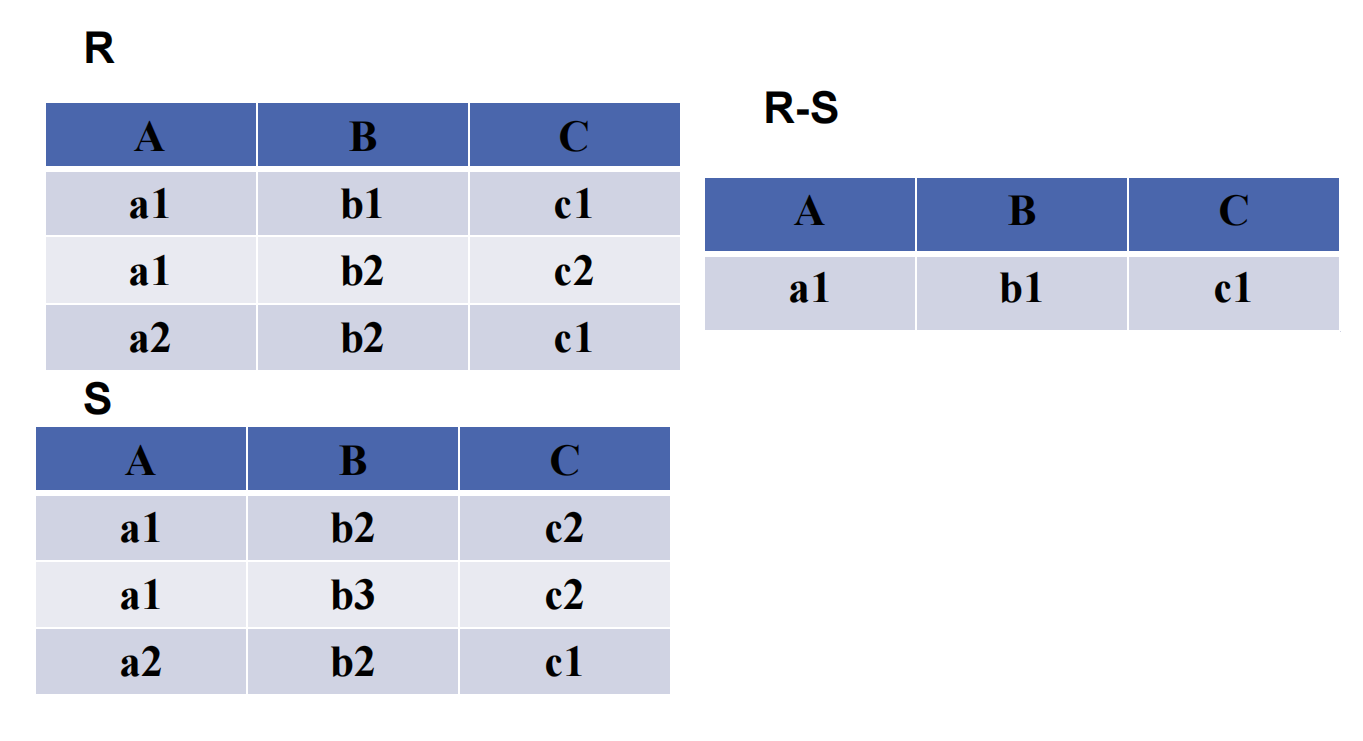
2.4.2 差 ( $ - $ )

要求跟并运算是一样的.
一个道理吗, 想作集合相减, 集合里面的东西首先得是同一类啊.

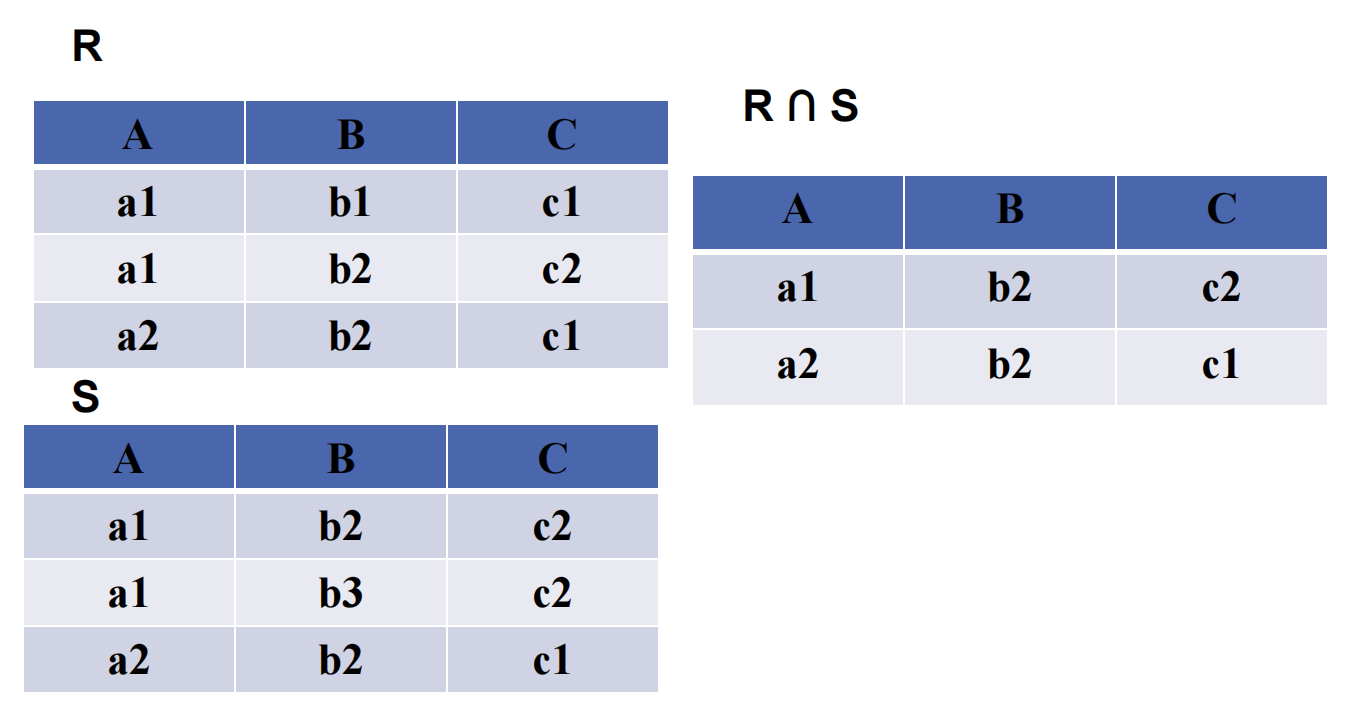
2.4.3 交 ( $ \cap $ )

要求跟前两者还是一样的, 不解释了哈.

这里还得单独提一嘴一个经典公式, 离散里面都说烂了:

$$ R \cap S = R - (R - S) $$

读者自行理解一下哈.

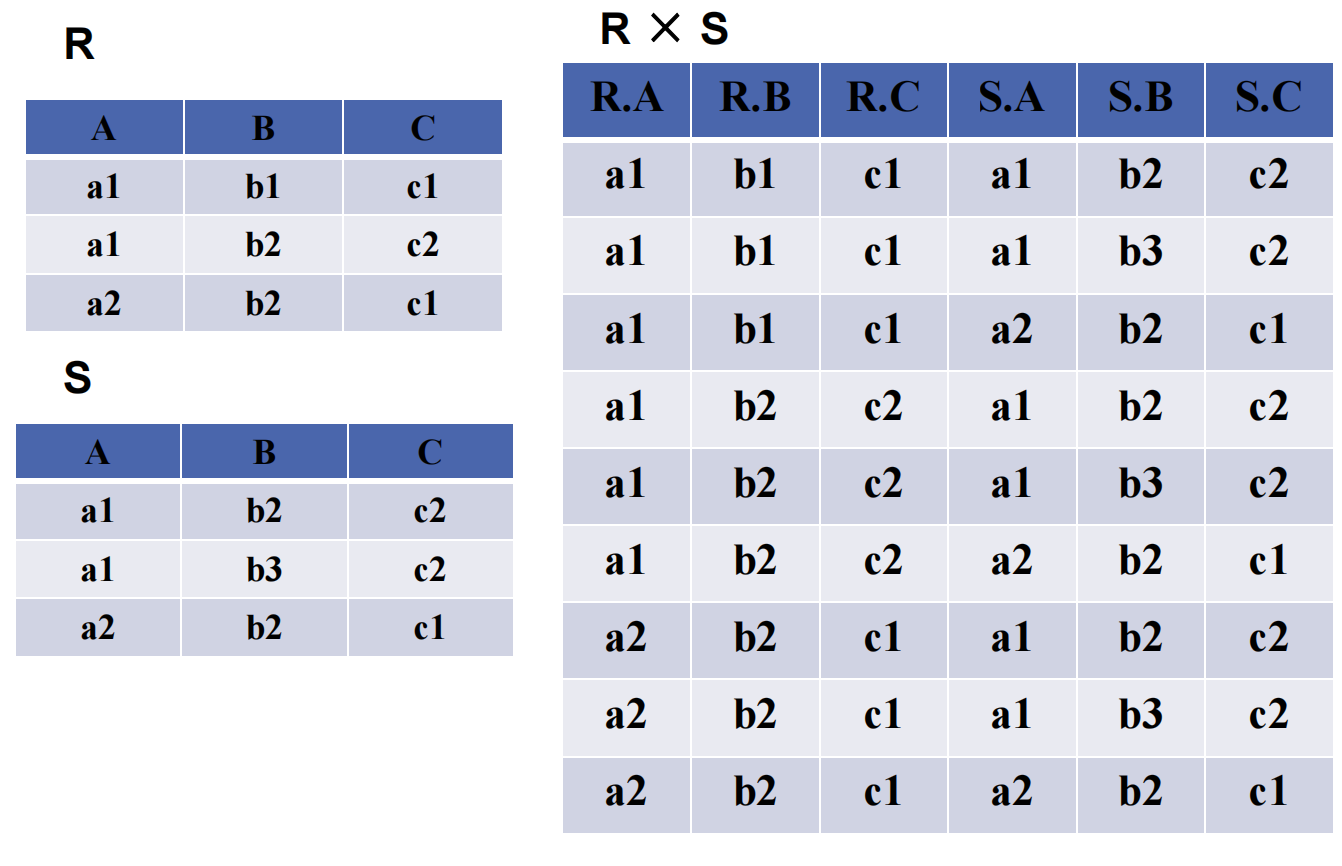
2.4.4 笛卡尔积 ( $ \times $ )

这个东西我们最开始唠叨元组关系那一堆事情的时候刚好说过.
在这里也就相当于把两个关系完全的排列组合了一下:

一个关系 $ R_1 $ , 目数 $ m $ , 共 $ k_1 $ 个元组
一个关系 $ R_2 $ , 目数 $ n $ , 共 $ k_2 $ 个元组

那 $ R_1 \times R_2 $ , 会有 $ m+n $ 目, 共 $ k_1 * k_2 $ 个元组.

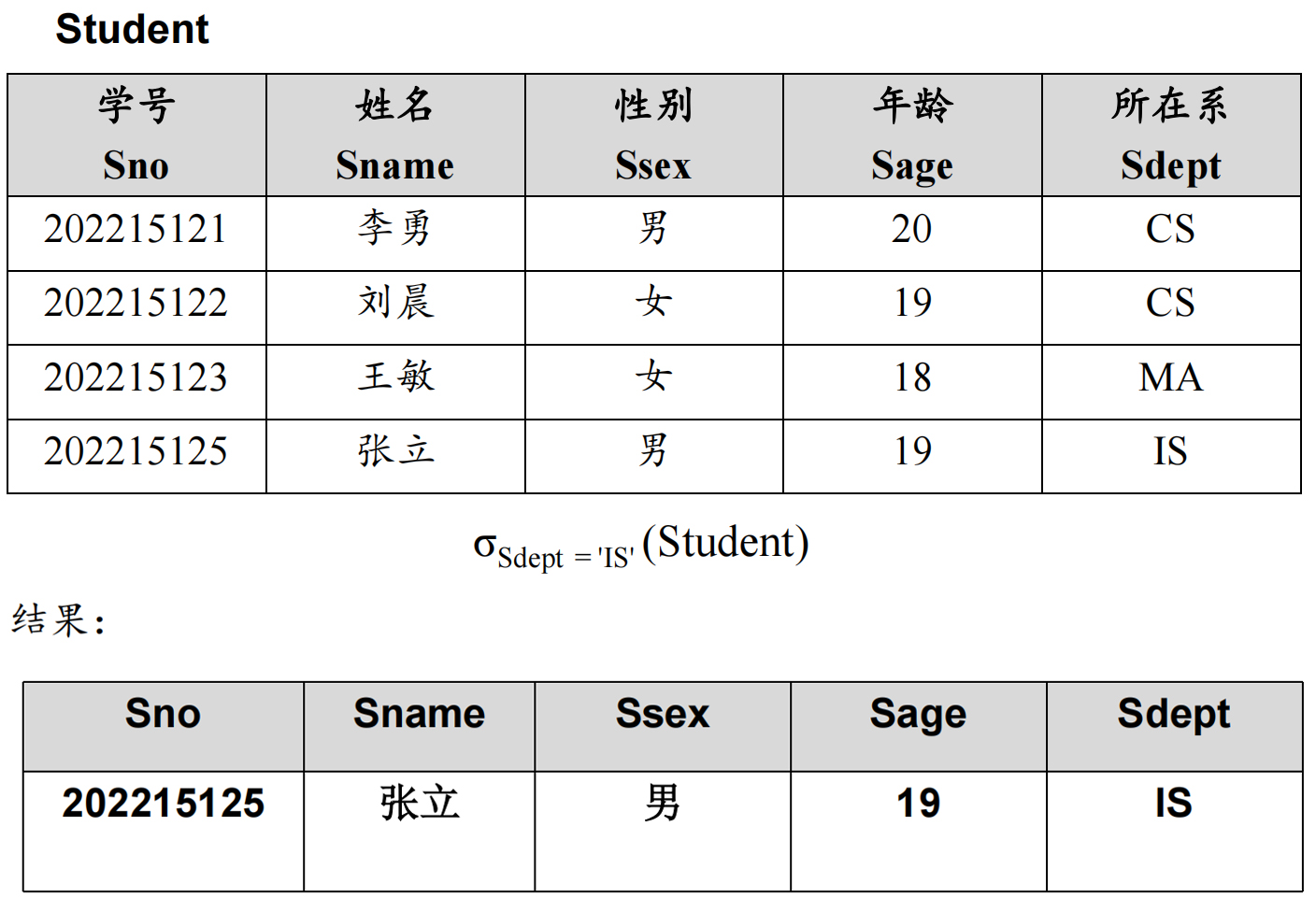
2.4.5 选择 ( $ \sigma $ )

选择, 如其所表示的, 就是针对 某一个表达式 对整个表进行筛选.

什么叫表达式?
比如关系 学生 中有个属性叫 学号

给出一个表达式: $ 学号 = 12345678 $ .
选择通常这样写 $ \sigma_{学号 = 12345678}(学生) $

所以给出更通用的写法:

$$ \sigma_{R.Attr_1 = x}(R) $$

就是在表R中选出满足这个条件的元组.

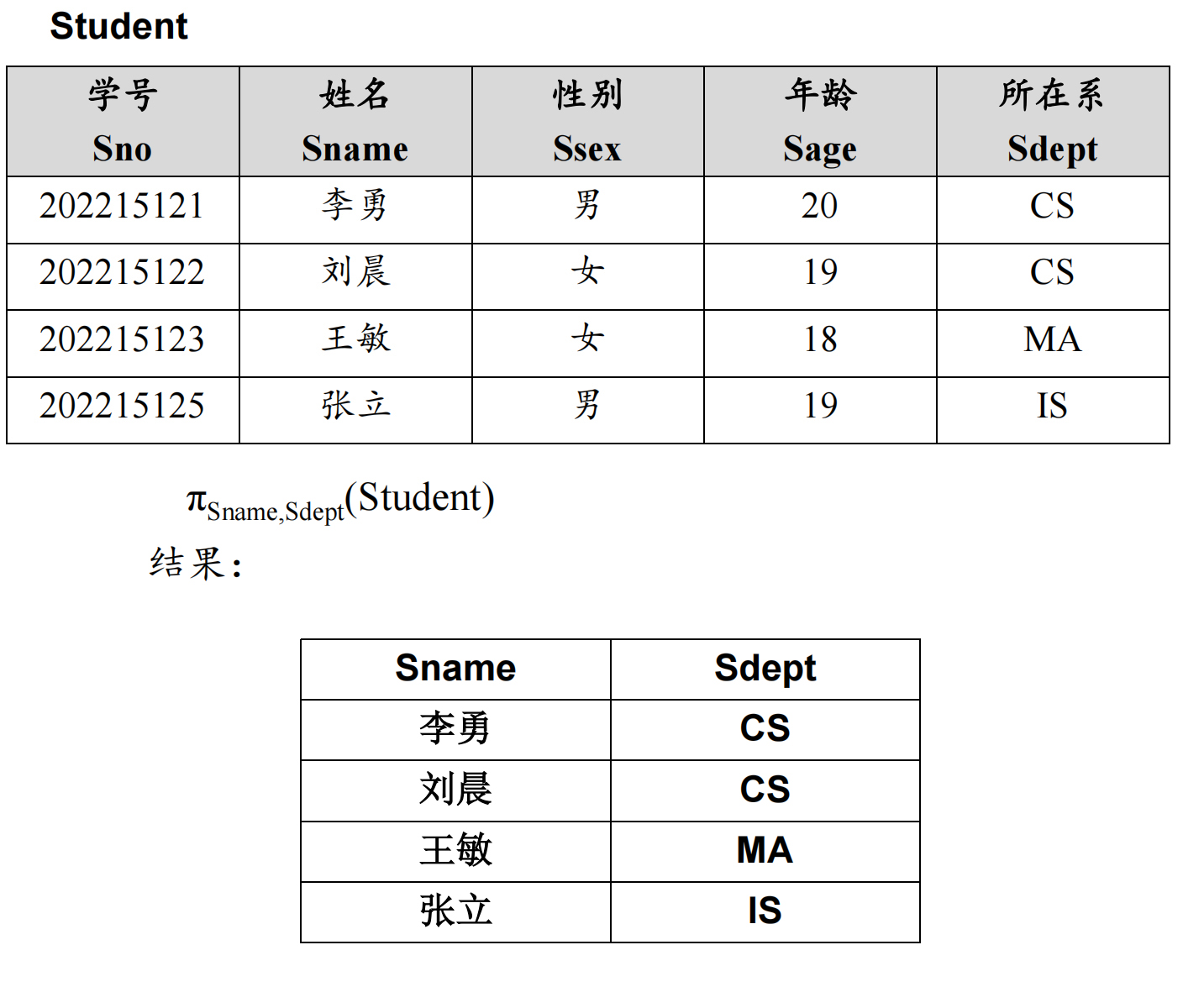
2.4.6 投影 ( $ \pi $ )

如果说选择是在元组(行)上做文章, 那么投影就是在属性(列)上做文章.
它的作用就是单独挑出某些列, 让它们单独形成一个表.

我们还是拿上面那个例子:
比如关系: 学生( 学号 , 姓名, 专业, 性别, 年龄)
我只想要姓名和专业这两行, 那就这么写: $ \pi_{姓名, 专业}(学生) $

给出更通用的写法:

$$ \pi_{R.Attr_{i1}, R.Attr_{i2}, …}(R) $$

就是在表R中把指出来的列但拉出来成一个表.

2.4.7 连接 ( $ \bowtie $ )

连接的概念是:

从两个关系的笛卡尔积中选择属性之间满足一定条件的元组

有点抽象, 先给个分类:

• 等值连接: 就是两个关系(表)的元组里面某个属性相等, 我就把这俩元组一块拉出来, 成一个新的元组.
• 自然连接: 是一种特殊的等值连接, 直接把结果里面的重复列去掉即可.

连接一般这么写:

• 一般连接

$$ R \underset{R.Attr_1 < S.Attr_2}{\bowtie} S $$

• 等值连接

$$ R \underset{R.Attr_1 = S.Attr_2}{\bowtie} S $$

• 自然连接

$$ R \bowtie S $$

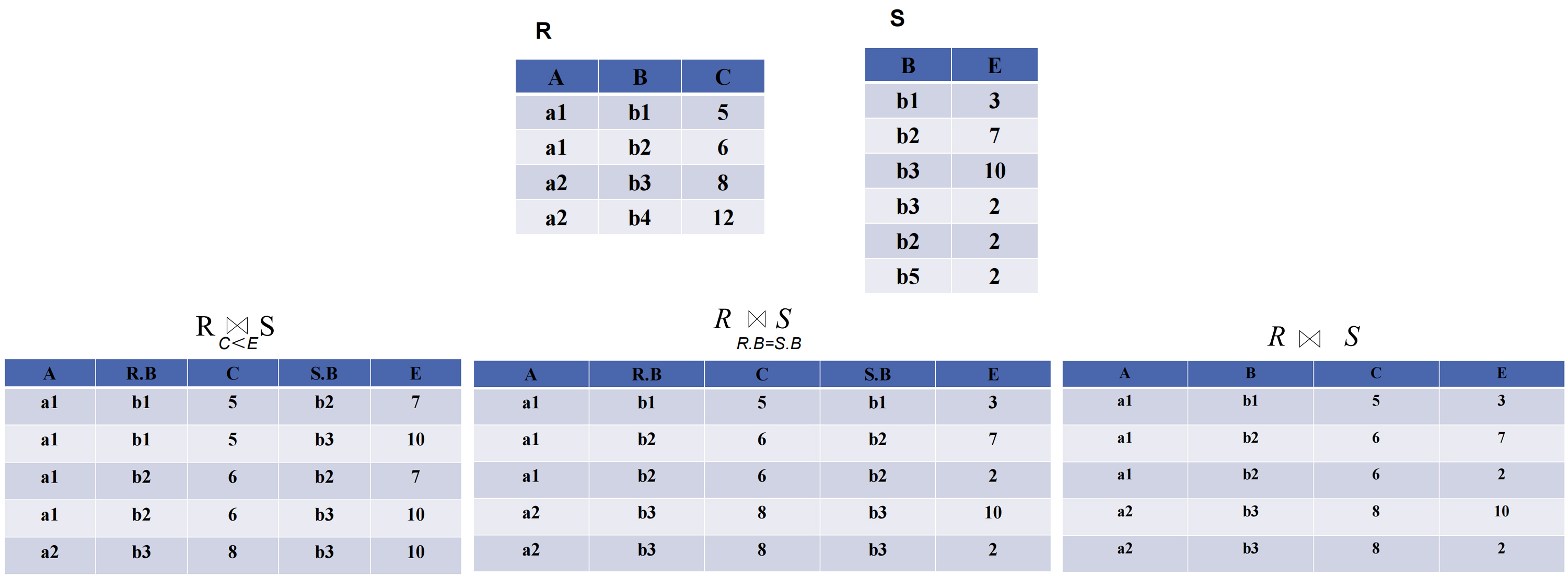
给个例子读者就应该能明白:

从上图可以看出来, 只有在做自然连接的时候才会删除重复的元组, 其它的连接方式不会 .

其实本来到这就结束了, 但是有个问题, 我们连接有时候不希望去掉一些元组的(尤其是自然连接的时候), 我们希望保留全部元组, 怎么办?
在自然连接的时候, 没有匹配的元组叫 悬浮元组 , 比如上图R中的 (a2, b4, 12) 和S中的 (b5, 2) .
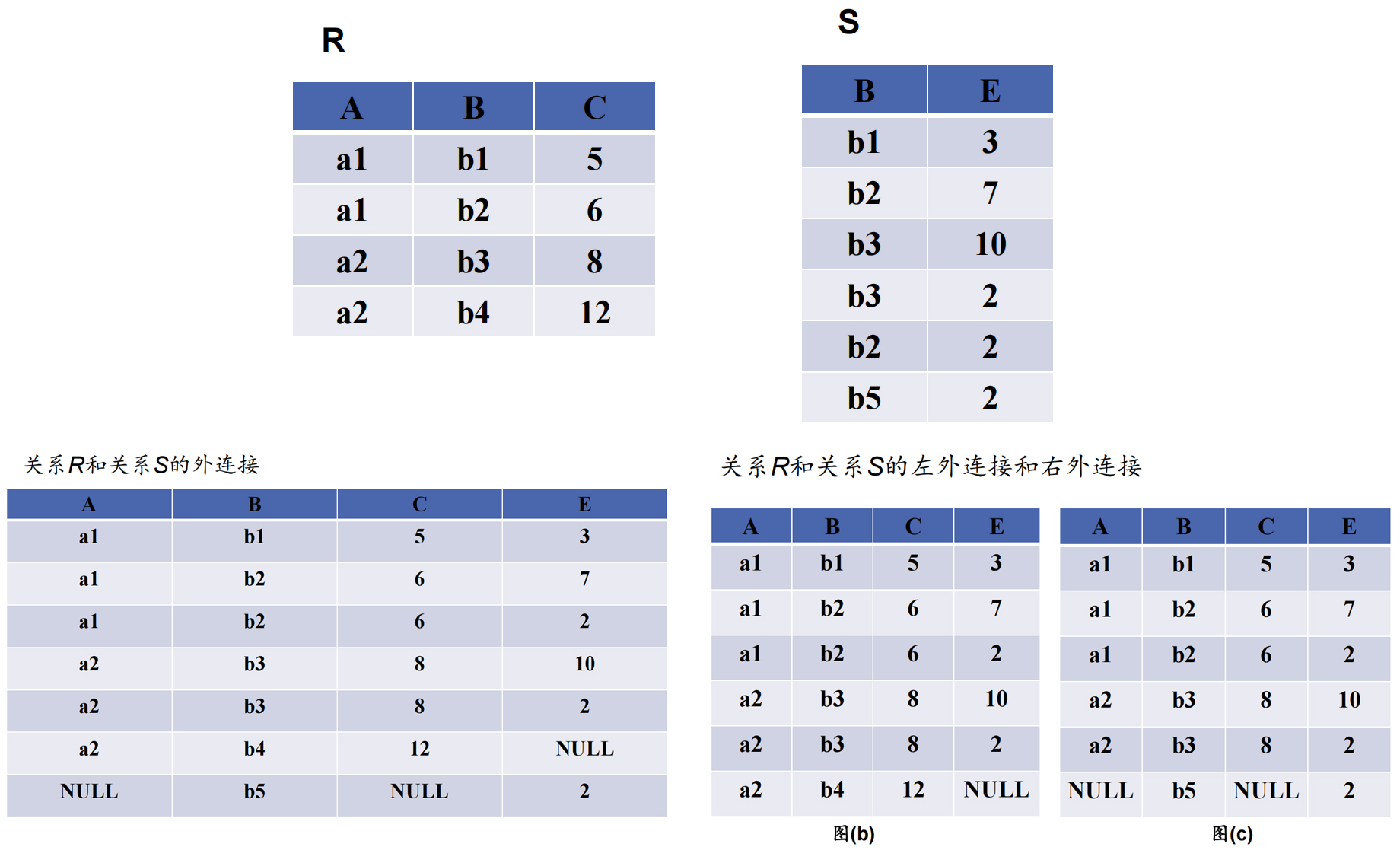
有个东西叫 外连接 . 会把所有的悬浮元组也放在表内, 并将没有匹配的属性填上空值.

对应的也有 左外连接 和 右外连接 , 就是只保留左边的 / 右边的悬浮元组.

2.4.8 除 ( $ \div $ )

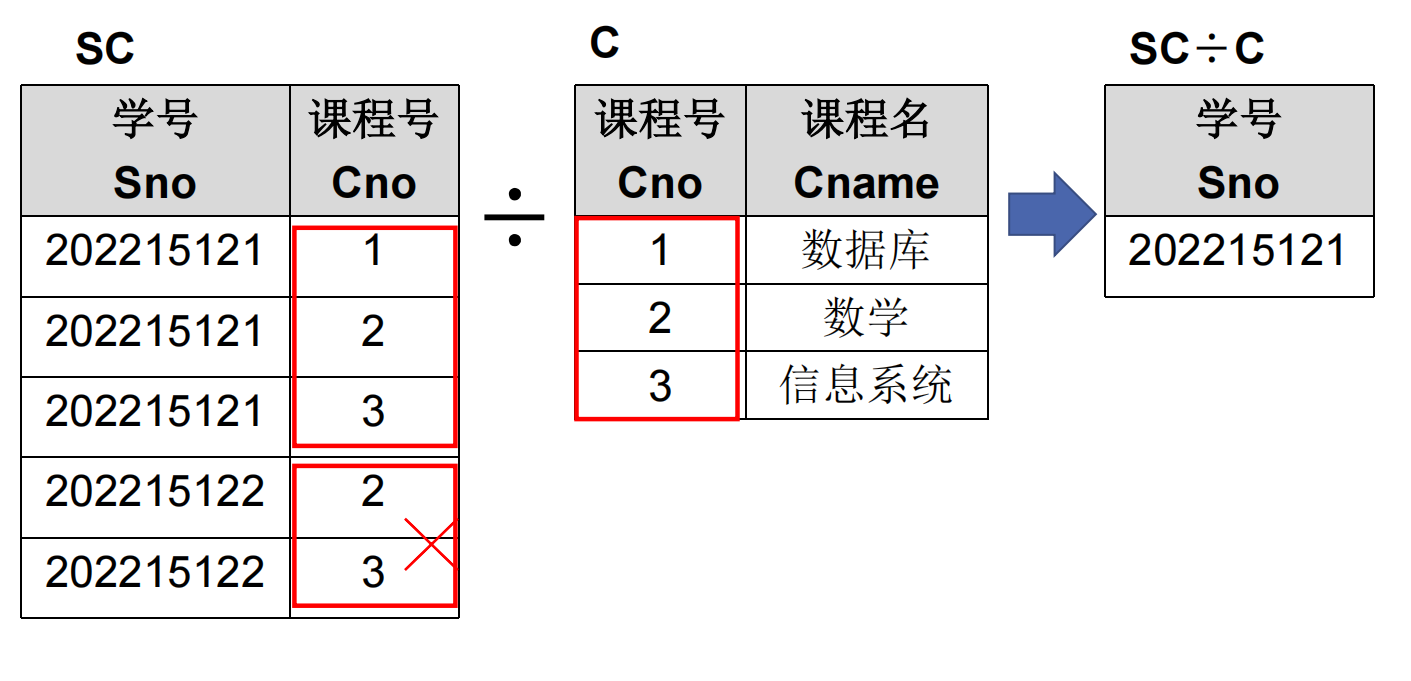
这是几个运算中最复杂的一个, 从定义来看这东西实在是不好讲. 本文中就不从定义出发了, 直接上例子.

其实就是在两个表中, 先对表R按照其它属性分组, 随后找到表R中的特定列满足表S某一列的筛选条件的组

显然, 能除的前提是:

• R中包含S的部分属性
• R中有一些属性不在S中