计算机网络 Chap.3 数据链路层

本系列计算机网络博文基于Bilibili王道的免费考研课程整理而来, 目的在于系统的梳理计算机专业课的基础知识, 并为将来的面试做好充分的准备.

除本系列外, 计算机考研相关还包括数据结构 / 操作系统 / 计算机组成原理的相关内容.

3.0 写在前面

本章的内容极其丰富, 因为王道考研的课程组织将很多后续章节中同样会涉及到的机制(流量控制, 差错控制, 可靠传输等)放到了数据链路层中一并讲解, 因此还请读者做好心理准备, 我们即将面对整个计网中最困难重重的一章(笑

不过也不必过于害怕, 啃完这一章, 后面的事情会轻松很多.

3.1 数据链路层的功能

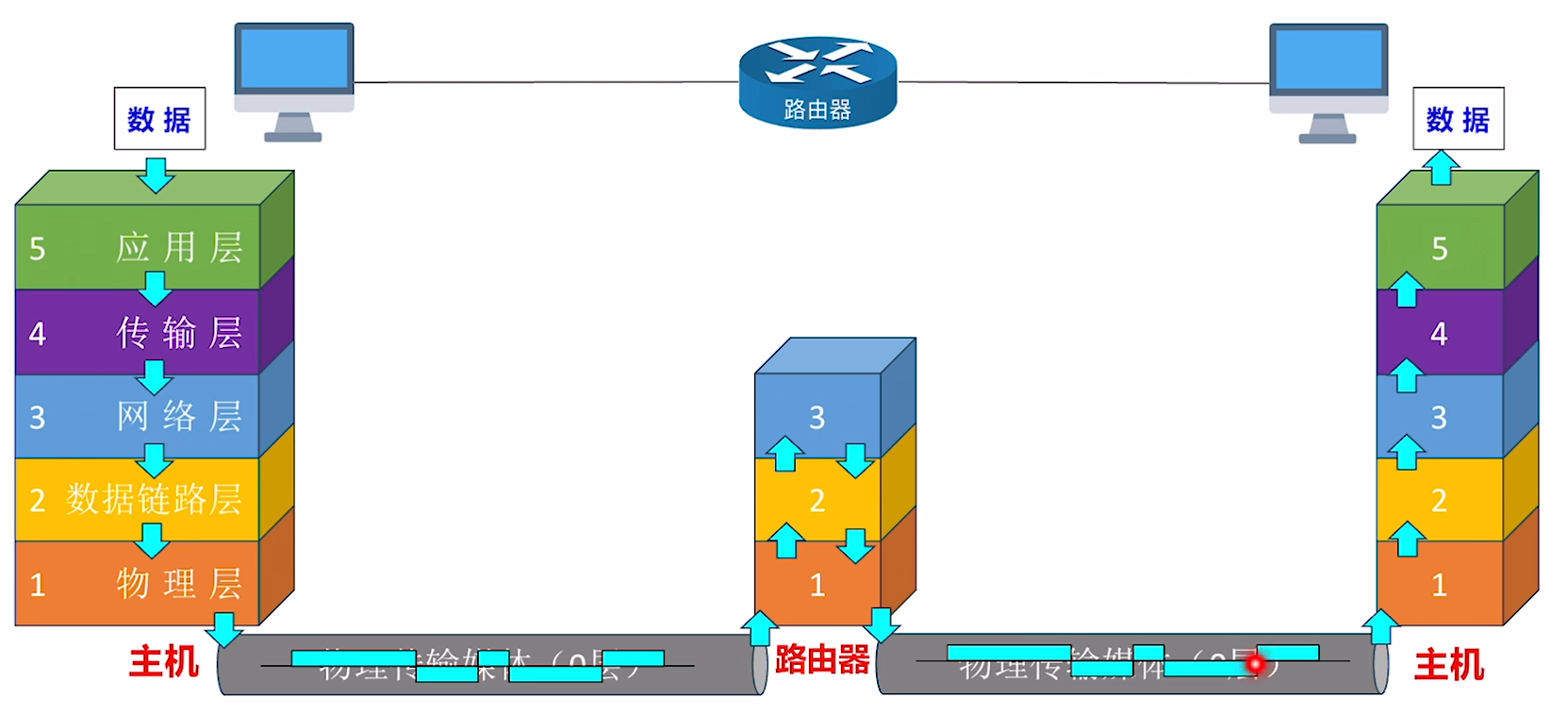
我们还是得把老图搬过来, 倒腾一下数据链路层的位置:

数据链路层上接网络层, 下接物理层. 因此其主要负责两件事:

• 使用物理层提供的 比特传输 服务
• 为网络层提供服务, 将网络层的 IP数据报(也就是分组) 封装成 帧 .

因此, 数据链路实际上, 为底层的物理层提供了一层额外的封装(就是这个 帧 ) , 它能够使得数据链路层在 物理链路 之上的 逻辑链路 上, 来进一步保证下层的数据传输的正确性.

这之后, 我们来详细一些, 列举一下数据链路层的主要功能:

• 组帧 / 拆帧
  • 帧定界: 让接收方能够确认帧的界限, 对应 组帧
  • 透明传输: 接收方的链路层要能够根据对方发送信息的定界来恢复原始的数据报, 即数据链路层的 服务数据单元 (SDU / Service Data Unit) , 并交付给其网络层. 对应 拆帧
• 差错控制
  • 需要能够发现一个帧内部的 位错误
  • 有 丢弃重传 / 纠错改正 两种策略, 前者简单些, 后者复杂些
• 可靠传输
  • 需要能够发现并解决 帧错误
  • 分为三种: 帧丢失 / 帧重复 / 帧失序
• 流量控制
  • 匹配发送方和接收方的发送 / 接收速率
• 介质访问控制
  • 对于 广播信道(总线型拓扑) , 需要实现介质访问权的分配
  • 对于 点对点信道 , 则通常不需要提供该功能, 因为存在专属介质, 不需要依靠介质的分配和争抢

注意: 差错控制 Vs 可靠传输
差错控制 通常针对的是 帧内部 的错误, 而 可靠传输 针对的是 帧之间 的错误.

这之后的小节中, 我们会对数据链路层实现这一大堆功能的方法进行逐一说明.

3.2 组帧

组帧 , 通常用于达成 帧定界 和 透明传输 的目的. 有四种常见的方案:

• 字符计数法
• 字节填充法
• 零比特填充法
• 违规编码法

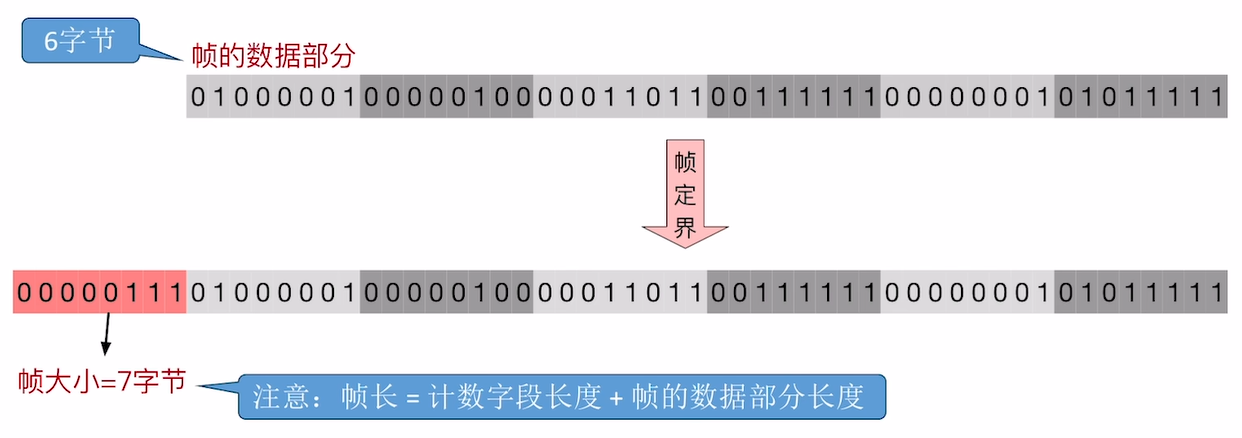
3.2.1 字符计数法

字符计数法 的原理是在每个帧的开头加上一个单独的 定长计数段 , 来表示每个帧的长度.

注意: 帧长
帧长, 指的是 计数字段长度和帧的数据部分长度的 总和 .

可知, 使用这种方法的帧的最大长度是有上限的, 其值为 $ 2^{计数字段长度}-1 $ .

除此之外, 该方案的 最大缺陷 在于: 任何一个计数字段出错, 都会导致后续全部的帧都无法正确定界 .

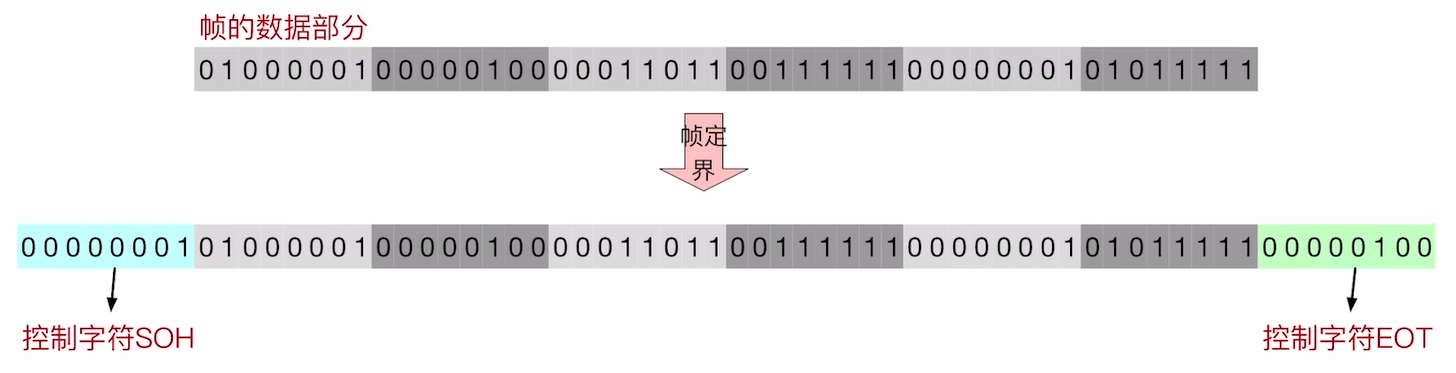
3.2.2 字节填充法

字节填充法 的原理是用两个规定好的字符来 标志一个帧的开始与结尾 . 它们分别叫 SOH(Start of Header) 和 EOT(End of Transmission) , 对应的16进制分别为 $ 01H $ 和 $ 04H $ .

这个方案也有问题, 因为当 数据内本身出现了SOH和EOT时 , 会使接收方 误认为该内容是控制字符 , 导致定界失败.

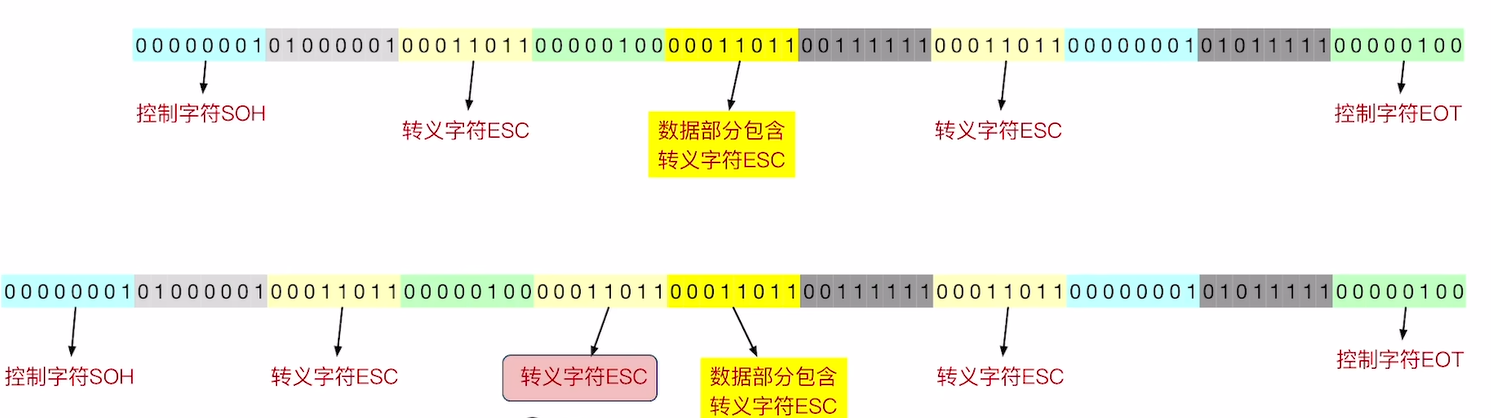
那咋办呢? 人们引入了一个新的字符叫 转义字符(ESC / Escape Character) , 对应的16进制为 $ 1BH $ .
如果发送方的数据中包含了 特殊字符(SOH, EOT, ESC) , 则需要在对应的字节之前插入一个转义字符, 同时接收方也会进行逆处理, 将数据中的转义字符删除, 并原封不动的保留其下一个字节的内容.

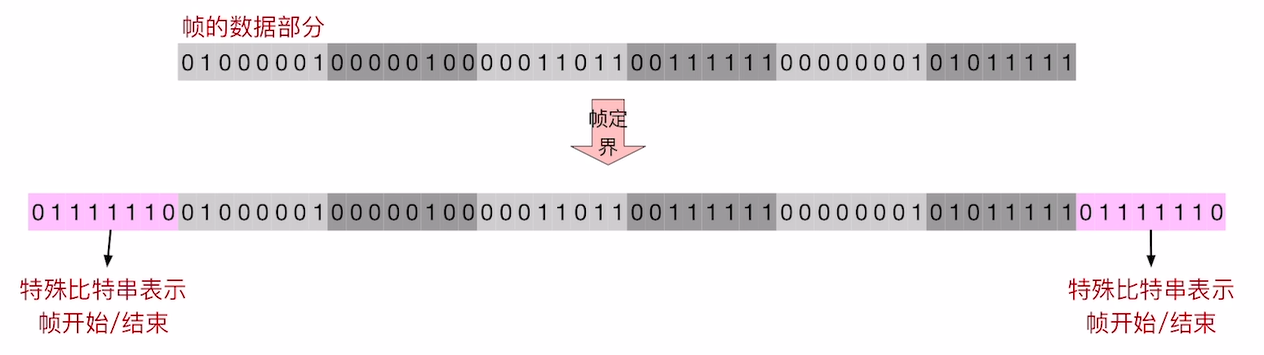
3.2.3 零比特填充法

这种方案的初心跟上一种类似, 只不过开头和结尾使用的定界符相同, 是 $ 7EH $ , 对应的二进制是 $ 0111,1110 $ .

如果理解了上一种方法的问题, 则很容易发现这种方式也面临着同样的问题. 数据本身如果包含完全相同的字节, 就出问题了.

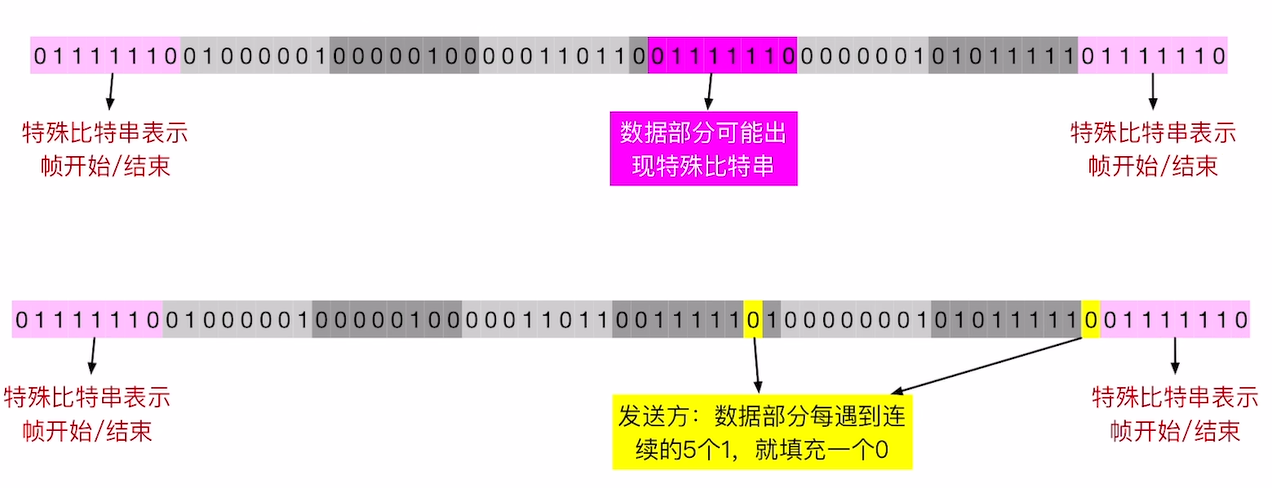
而这个方法中没有引入转移字符, 而是利用了 其规定定界符的特殊性 :

• 发送方对数据进行处理, 每当连续遇到5个1, 就 添加一个0 .
• 接收方对数据进行逆处理, 每当连续遇到5个1, 就 删掉后面的0 .

经过这样的处理, 能够保证数据中一定不会出现跟定界符一样的 六个1连在一块 的情况.

这种组帧方式极为常用, 因为它能够很快速的依赖硬件完成处理. 在当前数据链路层的两个主流协议( HDLC, PPP )中均有所采用.

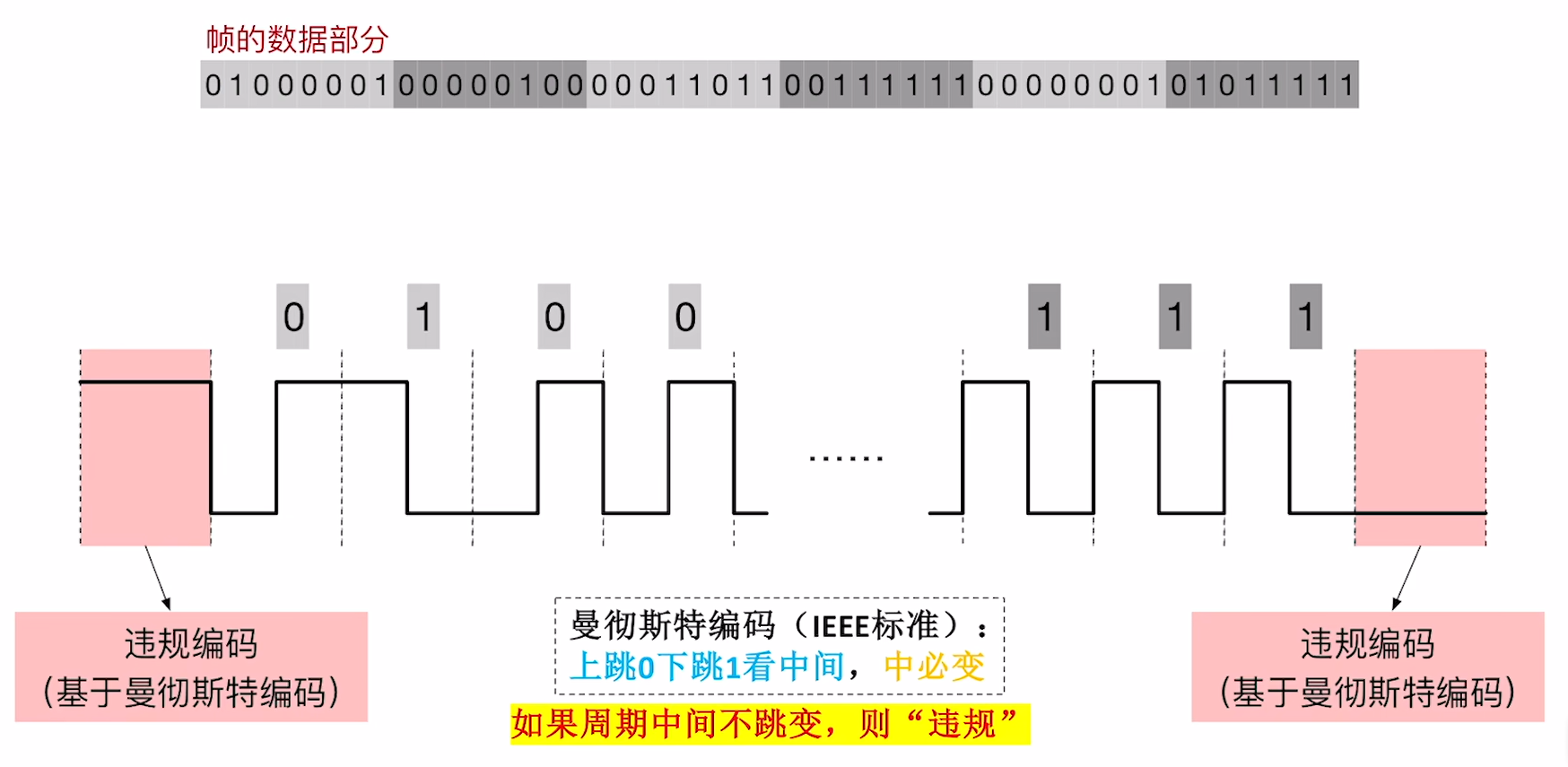
3.2.4 违规编码法

既然扯到 编码 了, 势必意味着这玩意需要物理层的配合. (不知道读者还记不记得上一章物理层的东西, 笑)

我们以 曼彻斯特编码 为例, 其每一个码元中间是必须要进行一次 跳变 的.
那么, 只需要让物理层在每一帧的前面和后面, 分别插入一个时钟周期的 违规信号(比如中间不跳变) , 就可以很方便地让接收方知道帧的起始位置和结束位置.

3.3 差错控制

差错控制 的目标是 发现并解决一个帧内部的位错误 . 解决方案通常有两种:

• 发现错误后丢弃帧, 并通知发送方重传.
  • 只需要发现错误即可, 检错编码
  • 奇偶校验码 / CRC循环冗余校验码等
• 发现错误并纠正比特错误
  • 需要能够确定是哪一位出了错, 纠错编码
  • 海明校验码

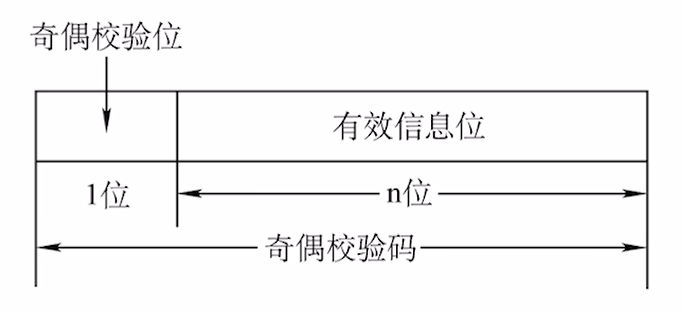
3.3.1 奇偶校验

奇偶校验 指的是通过一个单独的比特位来保证信息中 “1” 的个数为奇 / 偶.

• 奇校验 : 添加该校验位后, 该校验码中总共有奇数个1.
• 偶校验 : 添加该校验位后, 该校验码中总共有偶数个1.

通常而言, 偶校验 要更加常用一些, 因为只需要通过模2加的情况就能简单的得到结果.

• 发送方只需要将 数据的所有位 全部以 异或 的方式相加就能得到偶校验位.
• 接收方只需要将 校验码的所有位 全部 异或 起来, 结果为1说明数据出错, 结果为0说明通过.

注意: 异或?
因为 异或 运算实际上相当于 模2加法 , 因此结果为1就说明有奇数个1相加, 为0则反之.

注意: 奇偶校验的限制
因为奇偶校验只能针对 “1” 数据位总数的奇偶性进行检测, 因此当 偶数个位发生错误时 , 则此时奇偶校验码会失效.

最后, 还请读者明确, 奇偶校验码没有纠错功能, 只有检错功能 .

3.3.2 循环冗余校验

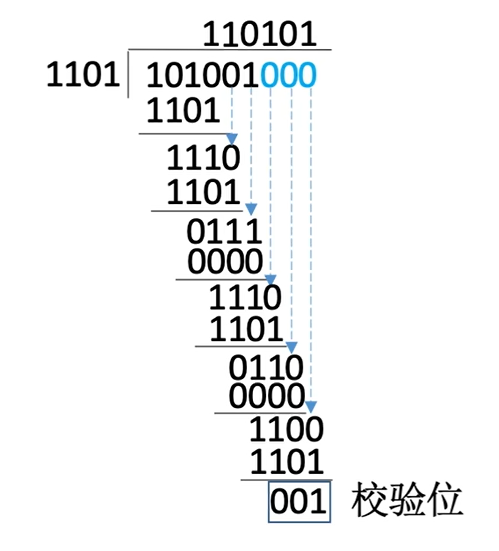
循环冗余校验(CRC / Cyclic Redundency Check) 的核心思路在于通信双方约定一个相同的 除数 , 随后对信息本身运行二进制除法来确定最终的 余数 .

其数据结构分如下两个部分:

• 信息位(K位) : 待校验的信息(也就是数据本身的位数)
• 校验位(R位) : 位数与校验码本身有关, 校验码通常由 生成多项式 给出, 而校验码的位数就是 生成多项式最高次项的次数

我们先捯饬明白一个问题: 生成多项式是什么 ?

生成多项式 是通过一个一元多项式来生成一段二进制的校验码的一种方法. 通过将该多项式各个次数项的系数拼接而成. 我们给个例子

$$ G(x) = x^3 + x^2 + 1 $$

则该多项式可以再写成: $ 1 \times x^3 + 1 \times x^2 + 0 \times x^1 + 1 \times x^0 $ , 进而写成二进制的 $ 1101 $ .

现在的问题是, 怎么除 ?

在循环冗余校验中, 采用的是 模2除 的策略. 其算法为 仅通过最高位判断当前位的商 , 后续低位则使用 异或 计算后顺延到下一次计算中.

我们给个例子, 假设信息位6位, 校验位3位(相当于最初直接将信息位左移3位):

最终得到的三位余数就是最终的 校验位结果 .

发送方计算得到这个校验码之后, 将 信息位 + 校验位 一并传输给接收方. 接收方收到后再次进行与发送方相同的运算, 并验证最终校验位是否为0即可.

注意: 接收方验证是否为0?
读者在这个位置可以类比一下除法的 余数 , 发送方发送给接收方的数据是 信息位 + 校验位 , 换句话说就是把发送方算出的余数加了上去, 再传给了接收方, 因此接收方在算相同的问题时, 只需要检验自己的运算结果是不是0即可.

这里需要额外提一嘴, 循环冗余校验 是具备纠错能力的 , 但具备纠错的条件是校验码能够表示的状态数 ( $ 2^R $ ) 大于本身的数据位数 (K+R) . 因此在计算机网络中一般不常用它来纠错而已.

通常, 循环冗余校验码能够检测出所有:

• 奇数位错误
• 双比特错误
• 小于等于校验位长度的错误

3.3.3 海明校验

海明校验 是对于偶校验的一种扩展. 他着眼于偶校验的校验码长度过短, 导致无法判断指定某位的错误.
那到底需要多少个校验位?

事实上上一节已经给出答案了, 如果校验位数为k, 则它总共能表示 $ 2^k $ 个状态, 这其中应当包括 n+k个信息位出错的情况 以及 正确的情况 . 即:

$$ 2^k \geq n+k+1 $$

我们给个例子:

4位信息位, 因此需要有3位校验码 ( $ 2^3 \geq 4+3+1 $ ) .
随后是海明码的位置规定, 校验位 $ P_i $ 应该放在数据位号为 $ 2^{i-1} $ 的位置上. (即校验位的分布是 1, 2, 4, 8, 16, …)
再将数据位分别填入剩余别的位置上.

这之后进入分组, 我们将 $ P_i $ 与 位置序号第i位为1的数据位分为同一组 .
对同一组的数据进行异或, 得到 $ P_i $ 的值(相当于进行 分组偶校验 )
那怎么纠错呢, 就是验证对应分组的偶校验是否正确, 得到 $ S_1, S_2, S_3, … $ , 这个值标志着哪一位的数据出了错.

请读者明确, 海明码具有 1位纠错 和 2位检错 的能力, 其中两位检错通常是通过前加全体偶校验提供的.

3.4 可靠传输与流量控制 / 滑动窗口机制

可靠传输 的目标是发现并解决 与帧整体相关的错误 , 具体分为三类:

• 帧丢失
• 帧重复
• 帧失序

注意: 差错控制中的丢弃重传
在 差错控制 一节中, 我们提到过有些校验码只具有检错的功能, 而并不能纠错, 这意味着接收方只能丢弃该帧并进行重传. 这种情况下, 问题就回到了可靠传输的 帧丢失 这一类中.

流量控制 的目标是让发送方控制自己的数据传输速度以 能够与接收方的接受速度相匹配 .

那为啥把这俩东西放一块唠呢?
因为这俩目标的实现都跟一个机制相关, 它叫 滑动窗口机制 .

3.4.1 滑动窗口机制

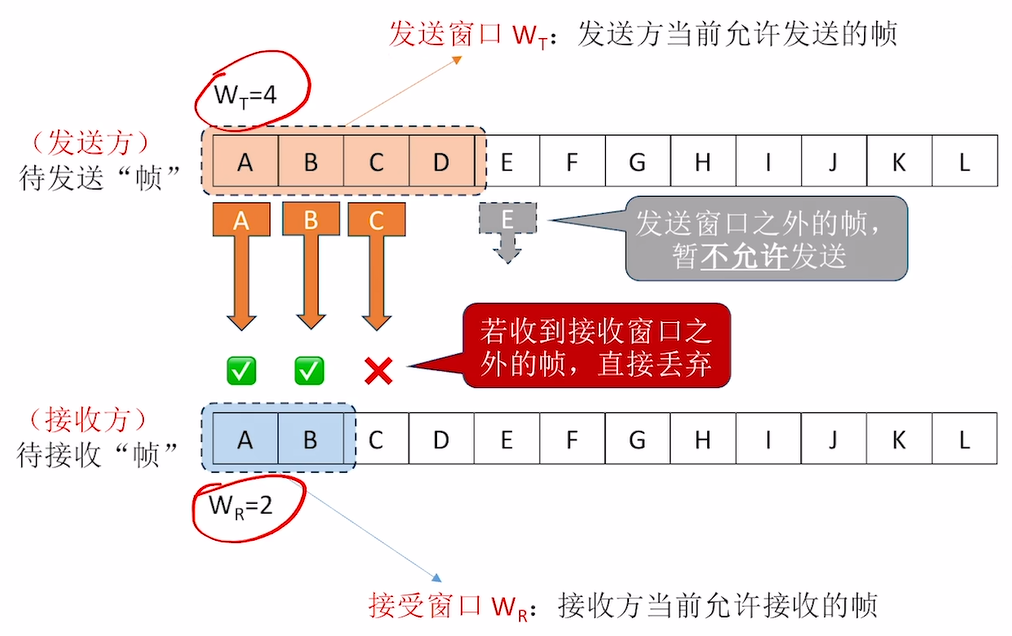
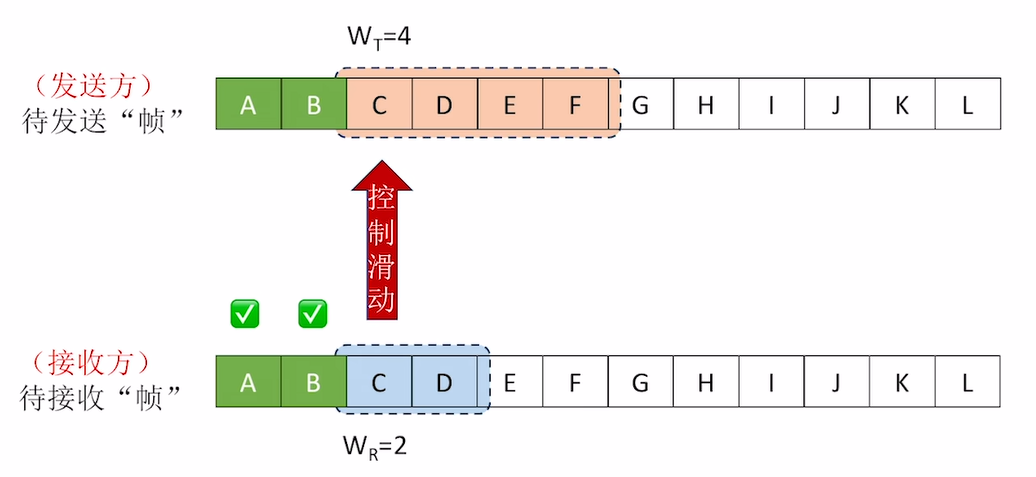
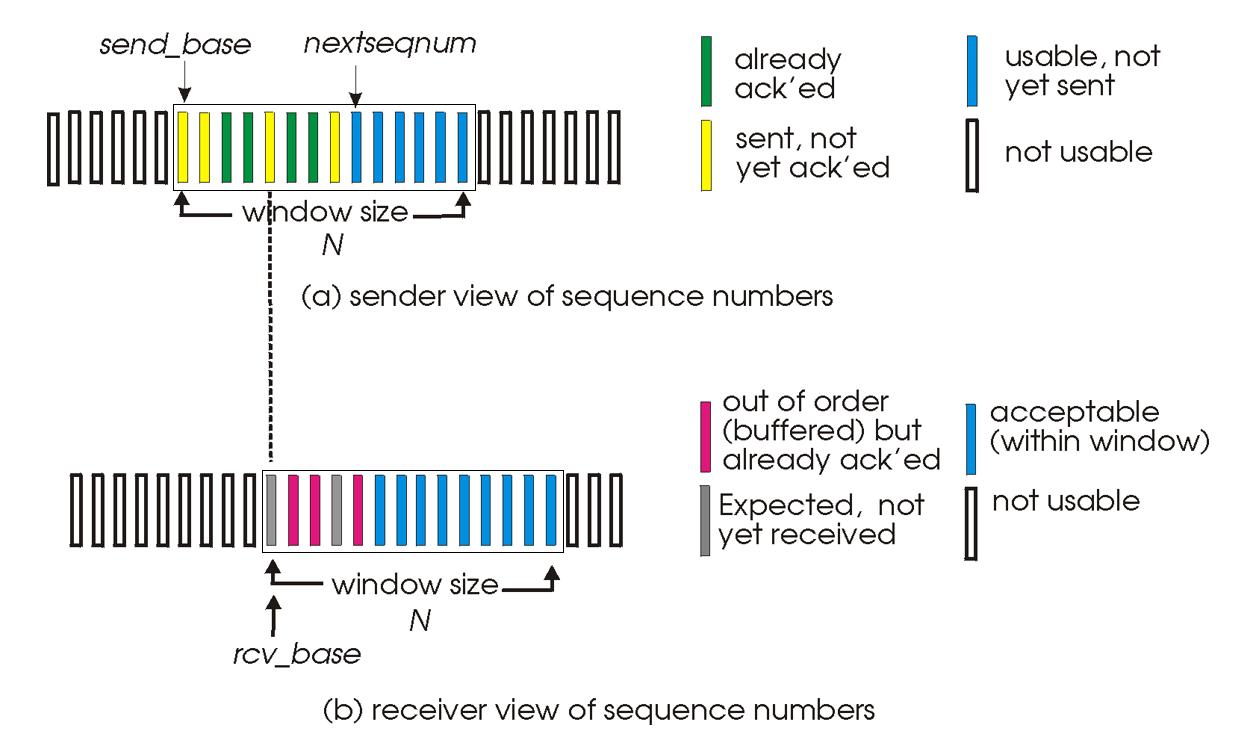
滑动窗口 是针对双方而言的, 它分为 发送窗口( $ W_t $ / Transmit Window) 和 接收窗口( $ W_r $ / Reveive Window) . 它们分别指 发送方当前允许发送的帧 和 接收方当前允许接收的帧 .

注意: 允许发送? 允许接收?
这一部分是笔者自己的理解, 如有错误还请读者谅解
个人认为对于发送 / 接收窗口的定义是有些模糊的, 从笔者的理解, 发送窗口包括了发送方当前 正在或准备传输但没能够接收到确认消息 的帧 , 而接收窗口包括了接收方当前 希望收到但还没有从发送方处收到的帧 .

因此, 发送方暂时不会发送在发送窗口外的帧, 而接收方也会拒绝接受在接收窗口外的帧.

那么, 窗口的 滑动 是如何体现的呢?

在 接收方收到滑动窗口内的帧时 , 会主动先将自己的窗口向后移, 随后通过某种确认方式向发送方确认 我已经收到这个帧了 , 发送方收到该确认消息后 , 也会主动将自己的发送窗口后移, 以达到同步的效果.

这样, 我们就大概明确了 滑动窗口 到底是个啥玩意.
随后我们要探讨的几个协议, 会在以下四个方面有所区别, 但请读者明确, 它们的本质都是滑动窗口机制的延申 .

• 窗口大小
• 确认机制
• 重传机制
• 帧编号

3.4.2 停止等待协议

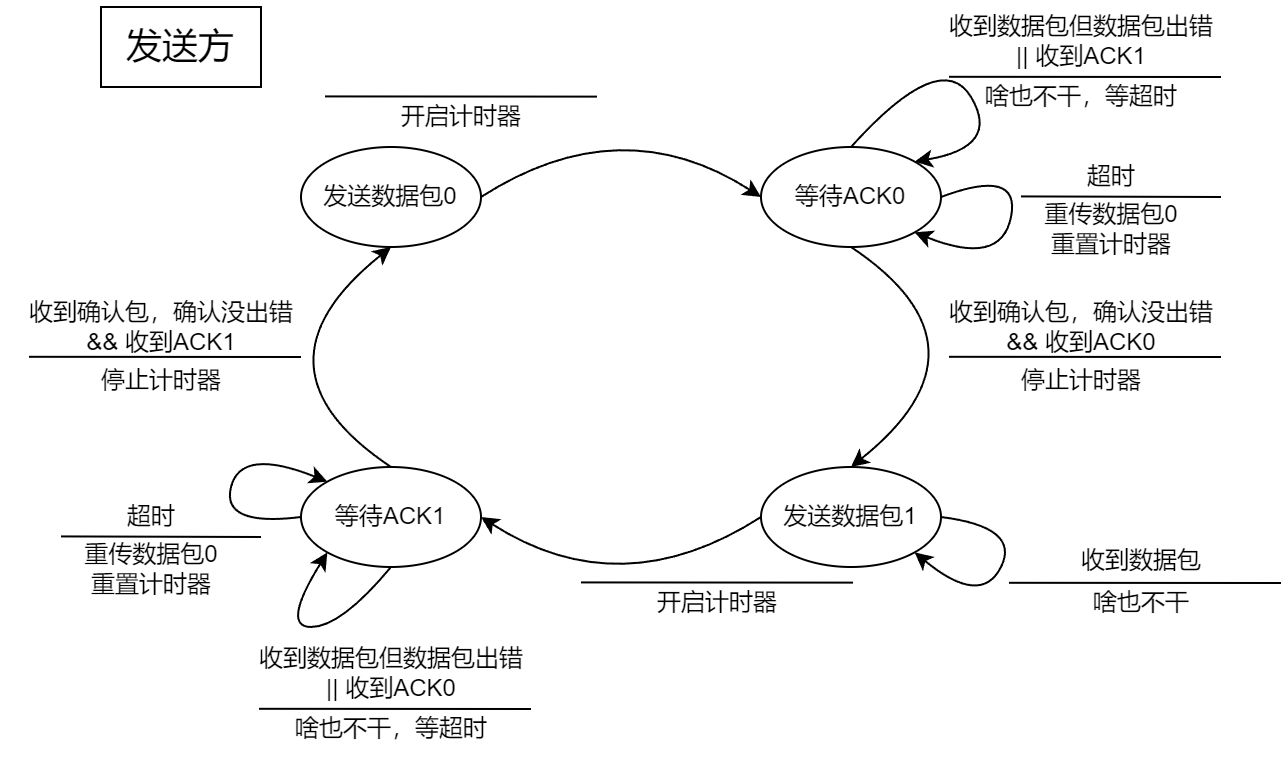
停止等待协议(SW / Stop and Wait) , 是滑动窗口机制中最为简单的协议.

它的特点如下所示:

• 窗口大小
  • 发送窗口 $ W_t = 1 $
  • 接收窗口 $ W_r = 1 $
• 确认机制
  • 接收方收到第i号帧, 且未检测出差错时, 发回给发送方一个确认消息 $ ACK_i $
• 重传机制
  • 发送方若超时未收到 $ ACK_i $ , 则主动重传该帧
• 帧编号
  • 仅需要1bit对帧进行编号

注意: ACK?
ACK 是 Acknowledge 的缩写, 在此后的协议书写中会经常使用.

在这里我们单独对 帧编号 进行一个说明.

帧的编号需要满足一个条件, 即 窗口长度必须小于等于序号空间大小的一半 .

$$ W_t / W_r \leq 2^{n-1} $$

这个式子在随后的协议中也会看到, 而在停等协议中, n=1就已能够满足该条件.

注意: 窗口长度的限制
这个位置王道的网课上给出的式子为 $ W_t + W_r \leq 2^n $ , 笔者认为这种写法不够严谨.
具体留给各位读者自行评判.

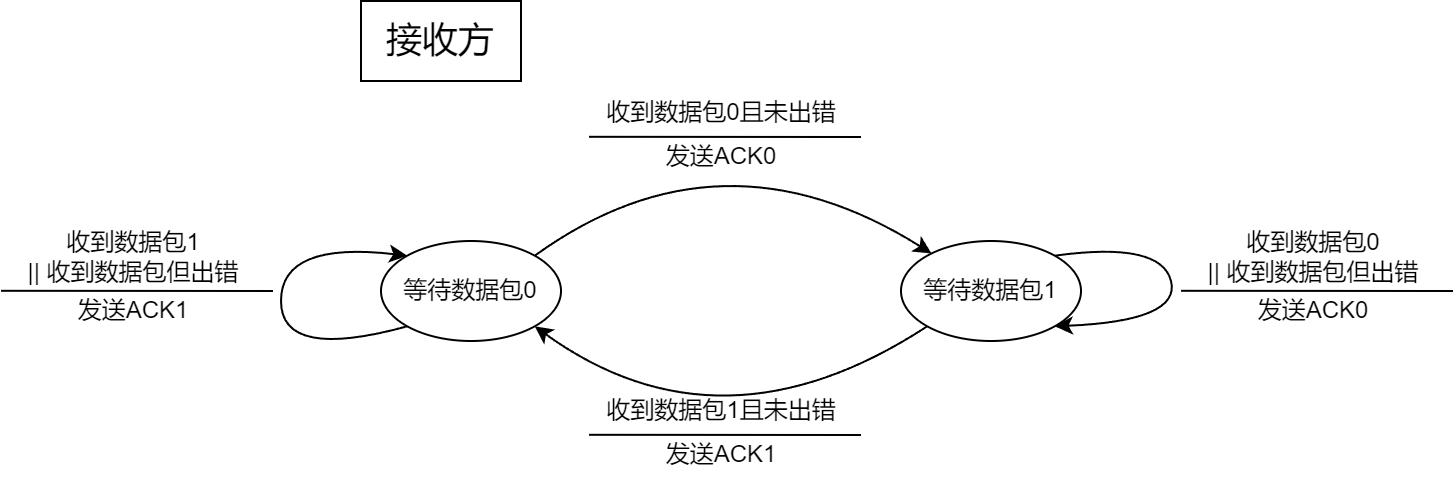
为了写清楚停等协议的具体步骤, 我们得画俩流程图 (草, 这东西真费劲啊)

我们对这种流程图进行一个说明:

• 圈内指的是 当前实体的状态
• 横线上是 当前实体收到的信息
• 横线下是 当前实体会采取的措施

总结一下停等的总体思路:

• 发送方发一个包, 等待接收方确认
• 接收方收到包, 发送确认消息, 等待发送方下一个包

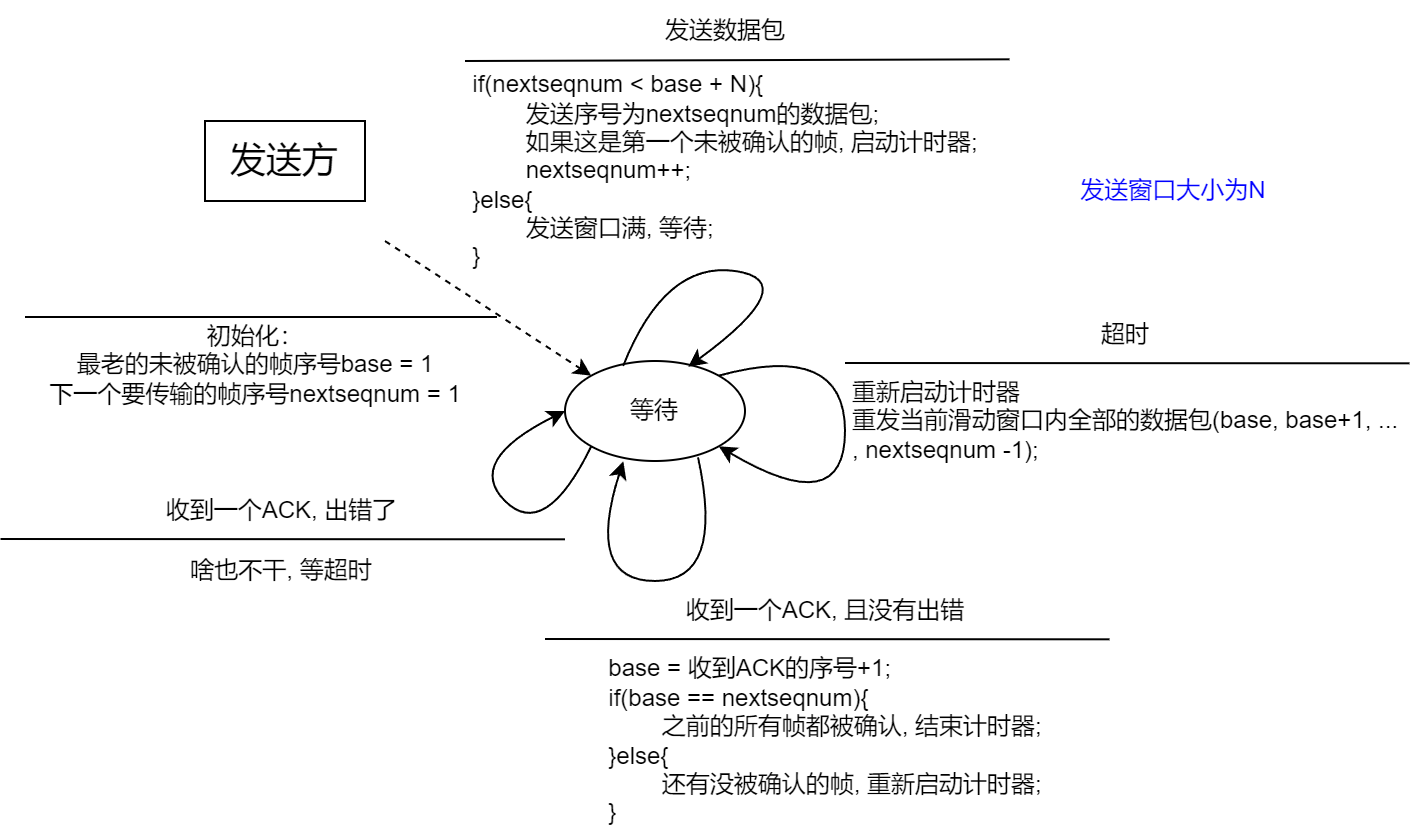
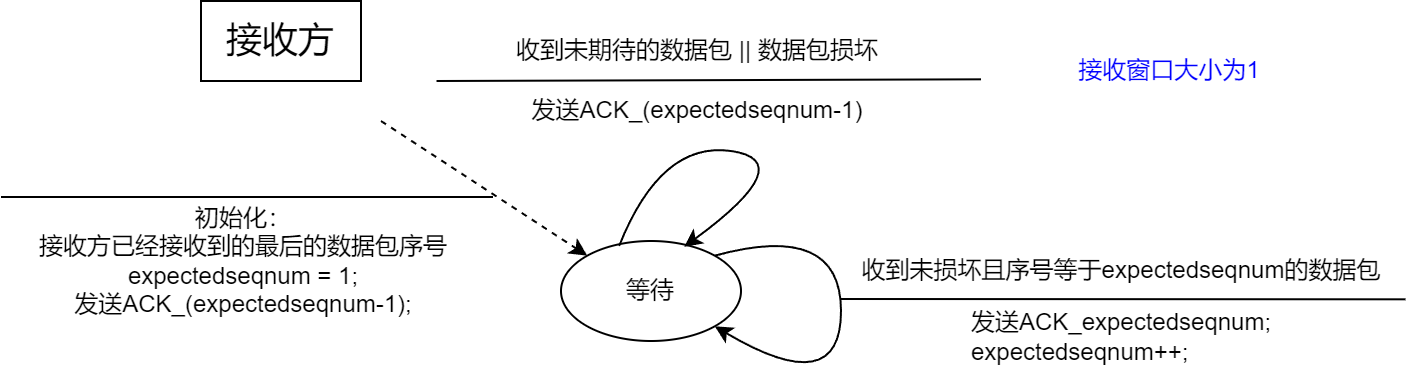
3.4.3 后退N步协议

后退N步协议(GBN / Go Back N) , 比停止等待协议要稍显复杂, 它的特点如下:

• 窗口大小:
  • 发送窗口 $ W_t > 1 $
  • 接收窗口 $ W_r = 1 $
• 确认机制
  • 接收方收到第i号帧, 且未检测出差错时, 发回给发送方一个确认消息 $ ACK_i $
• 重传机制
  • 发送方若超时未收到 $ ACK_i $ , 则主动重传该i号帧
• 帧编号
  • 仅需要1bit对帧进行编号
• 特殊规则
  • 接收方可以 累计确认 . 即连续收到多个数据帧时, 只返回最后一个收到的帧的ACK
  • 如果发送方超时未收到i号帧的ACK, 则重传 i号帧以及其之后的所有帧

意义即接收方能够通过 $ ACK_i $ 表示自己已经收到第i号帧以及其之前的所有帧.

我们同样通过两个流程图来分别说明发送方和接收方的事情:

后退N步的主要想法是让发送方能够 一次发送多个帧 , 而不用发一个等一下这样循环, 提高信道利用率.
但可以预见的是, 如果 信道错误率很高 , 或者 接收方接收速率很慢 的情况下, 发送方需要 频繁的后退 , 这也会导致资源的浪费.

3.4.4 选择重传协议

选择重传协议(SR / Selective Repeat) , 尝试解决GBN的缺点. 它的特点如下:

• 窗口大小:
  • 发送窗口 $ W_t > 1 $
  • 接收窗口 $ W_r > 1 $
• 确认机制
  • 接收方收到第i号帧, 且未检测出差错时, 发回给发送方一个确认消息 $ ACK_i $
• 重传机制
  • 发送方若超时未收到 $ ACK_i $ , 则主动重传该i号帧
• 帧编号
  • 仅需要1bit对帧进行编号
• 特殊规则
  • 接收窗口不能大于发送窗口
  • 接收方逐个确认已收到的分组
  • 发送方只重新发送没有收到ACK的分组
  • 发送方对每个分组均有单独的计时器

注意: 选择重传的机制
王道网课给出的选择重传机制与笔者教材(计算机网络: 自顶向下方法 / Computer Networking: A Top-Down Approach)中的机制并不相同, 甚至可以说是差异明显. 笔者这里给出的是教材中的方法. 如果读者有兴趣, 可以前往 选择重传协议王道网课版 进行王道版本的学习.

3.4.5 三种协议的信道利用率

三种协议唠叨完了, 我们看看它们的优劣, 那自然就要捯饬一下它们对于信道的利用程度对吧.

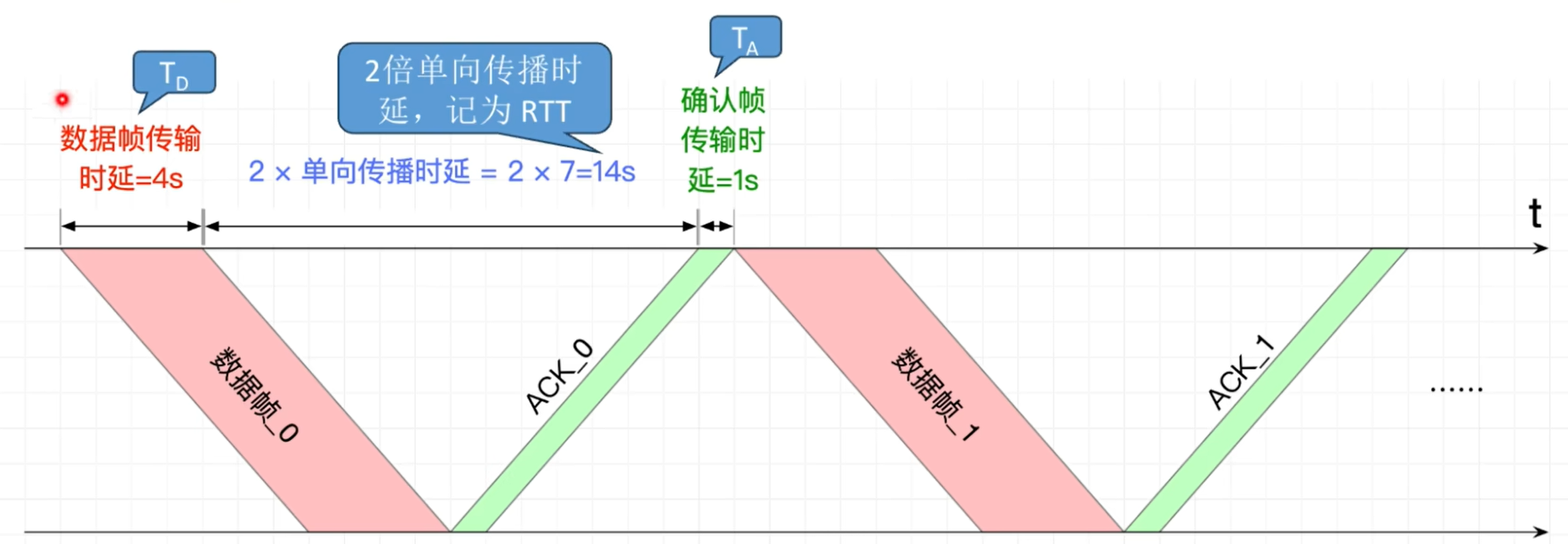
3.4.5.1 停等协议的信道利用率

我们先从最简单的 停等协议 开始.

可见, 停等协议的一个周期由三部分组成:

• 数据帧传输时延 $ T_D $
• 传播时延: $ RTT $
• 确认帧传输时延 $ T_A $

因此我们能给出这么个式子:

$$ U = \frac{T_D}{T_D + RTT + T_A} $$

注意: 信道利用率的计算前提
我们在本处计算信道利用率时的前提是 理想情况 , 即信道不丢帧, 不产生比特差错的情况. 原因在于如果我们加上那些意外, 整个情况会显得非常复杂 (那不乱套了嘛)

注意: RTT Vs 单向传播时延
事实上, RTT = 2 * 单向传播时延 , 请读者务必注意这个名称问题

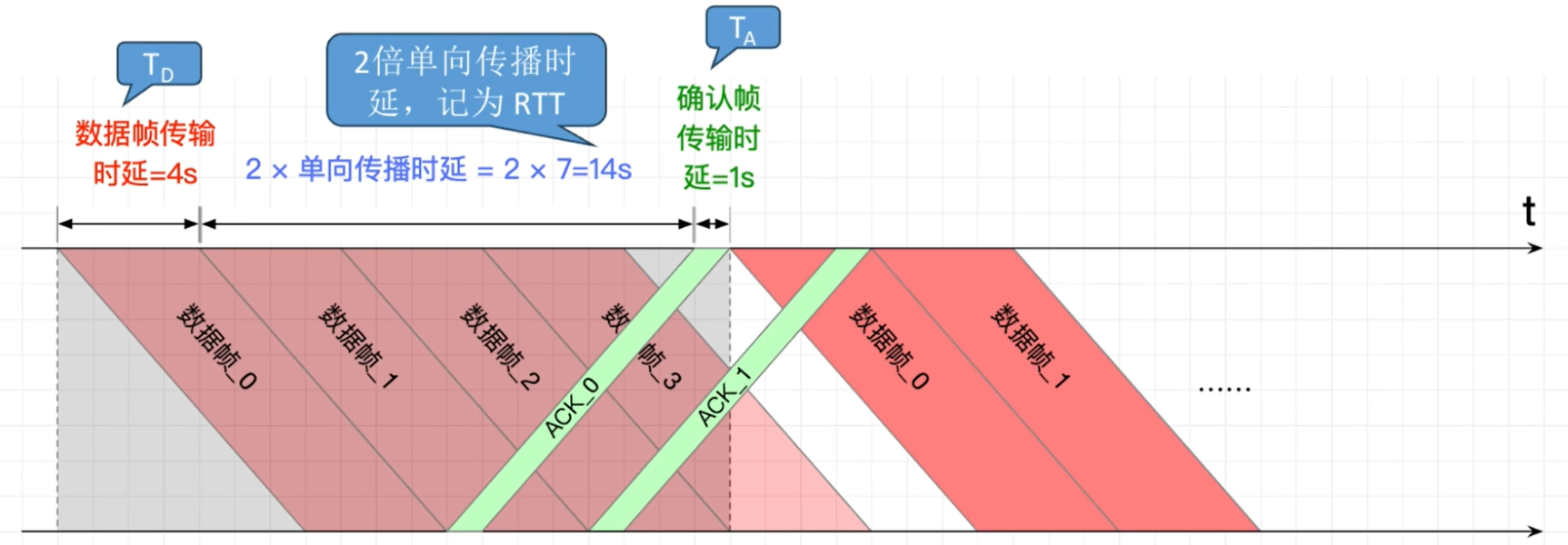
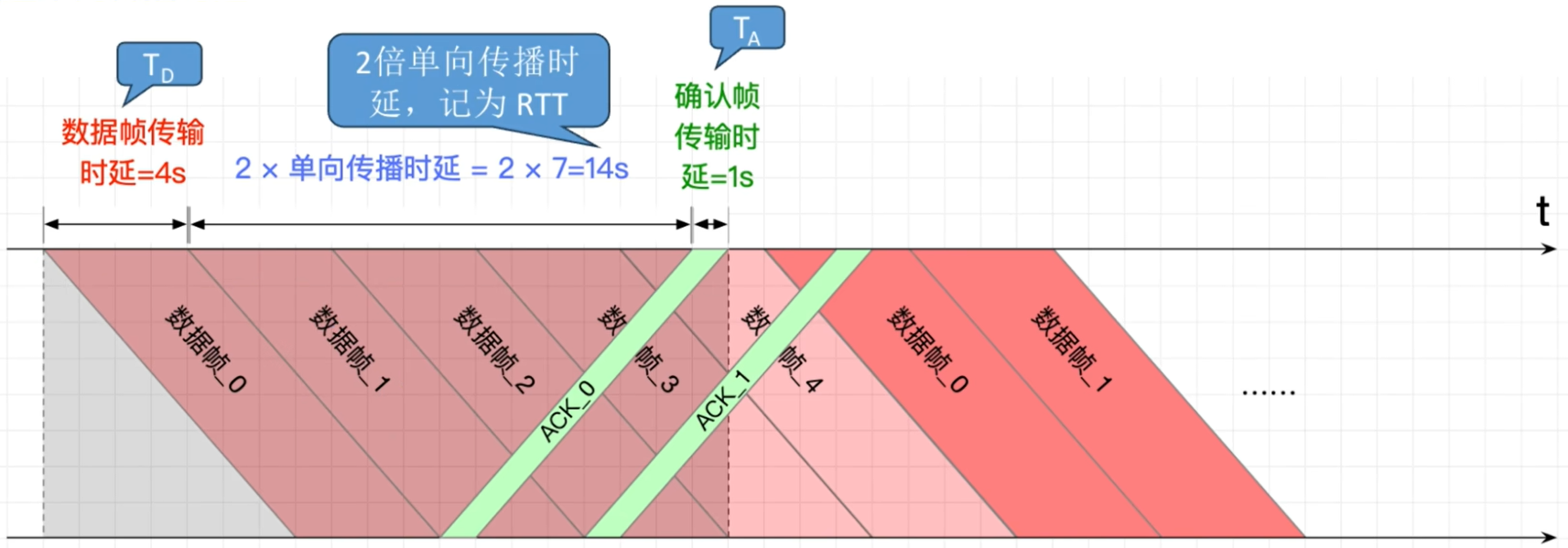
3.4.5.2 GBN / SR 的信道利用率

接下来是复杂一些的 回退N步和选择重传协议 , 之所以把他俩放在一块说, 是因为他俩的理想条件是几乎完全一致的, 即发送一帧后对方也能及时接收这一帧并返回ACK.

我们只需要看单个周期内(即灰色框内部)的信道利用率, 其实组成是一致的, 只不过此时的情况在于, 发送方能一次发送多个帧对吧. 进而我们给出这个式子:

$$ U = \frac{N * T_D}{T_D + RTT + T_A} $$

其中, N 是指 发送过程中能够连续发送的数据帧数目 .

相信有些读者读到这已经有点想法了, 那如果我的发送数据的这 $ N * T_D $ 比你的分子还大捏? 你这式子不炸缸了吗?

所以说嘛, 都叫信道利用率了, 还能比1大不成? 算出来大于1直接写1就完了.

3.4.6 额外补充

有三个名词需要读者了解:

• 滑动窗口协议: 指GBN或SR
• ARQ(Automatic Repeat Request / 自动重传请求)协议: 指ST / GBN / SR
• 连续ARQ协议: 指GBN / SR

3.5 信道划分与介质访问控制

首当其冲, 什么是介质访问控制 ?

概念: 介质访问控制
为了应对多个节点共享信道时的 信号冲突 , 对各个节点对传输介质的访问进行控制的过程.

好嘞, 所以说白了就是该怎么应对介质访问冲突对吧, 那我们来慢慢寻思.

3.5.1 信道划分

我们先从最基础的, 单信道的访问控制聊起.

3.5.1.1 时分复用

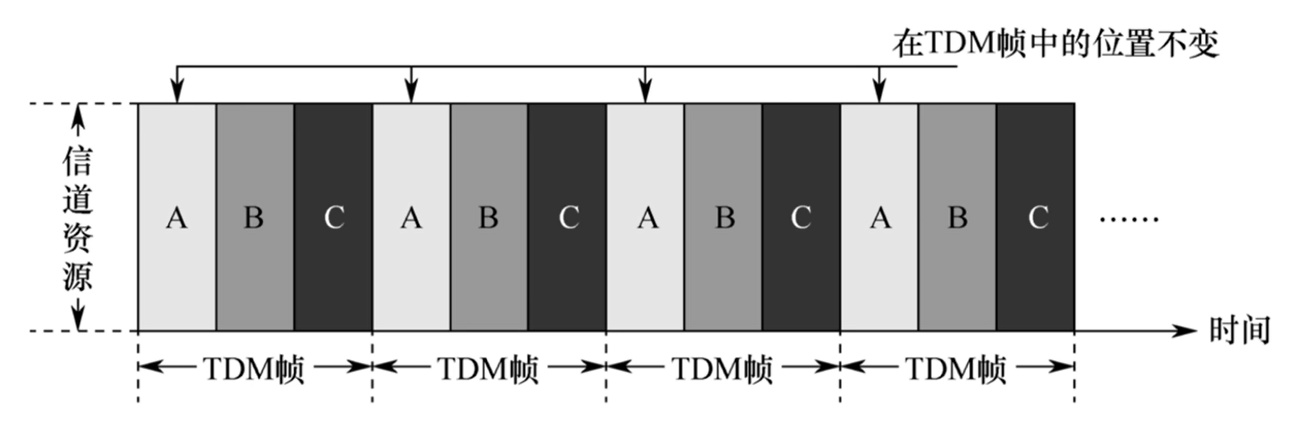
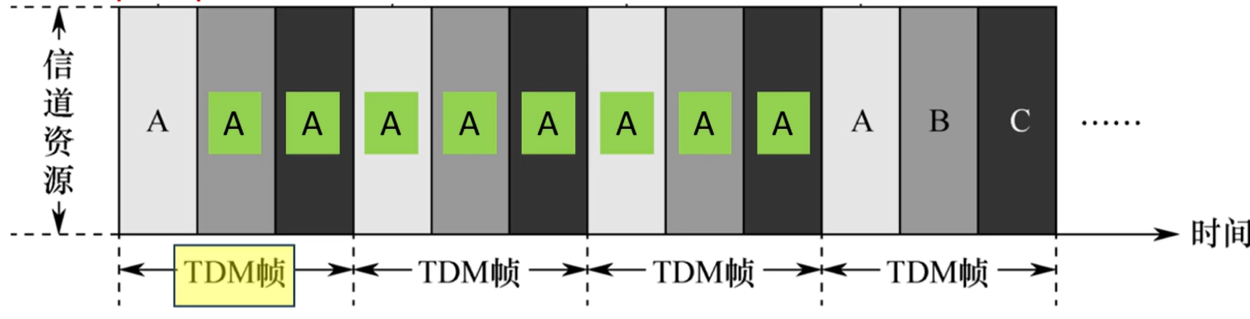
概念: 时分复用(Time Division Multiplexing, TDM)
将时间分为等长的 TDM帧 , 同时每个TDM帧又被分为等长的 m 个 时隙 . 将m个时隙分别分配给各个用户使用.

时分复用非常公平, 有时候显得有些公平过头了.

• 每个节点最多享受到信道传输速率的 $ \frac{1}{m} $
• 当有节点在它的时隙内不需要发送信息时, 该信道的资源会被浪费.

3.5.1.2 统计时分复用

概念: 统计时分复用(Statistic Time Division Multiplexing, STDM)
亦称 异步时分复用 , 在TDM的基础上, 动态按需分配时隙.

3.5.1.3 频分复用

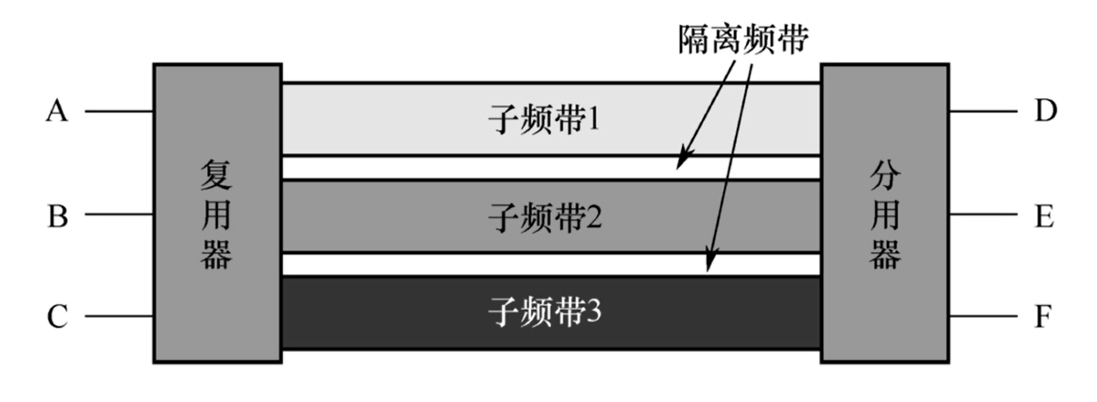
概念: 频分复用(Frequency Division Multiplexing, SDM)
将信道的总频带划分为多个 子频带 , 每个子频带都作为一个子信道. 每对用户使用其中一个子频带进行通信.

上图中出现了两个陌生的玩意:

• 复用器 : 将各个节点发出的信号 复合 后传输到共享信道上.
• 分用器 : 将各个子频带的信号 分离 出来.

注意: 隔离频带
都分频了, 那自然要做一些隔离措施, 防止分用器将本不属于这个子频带的信号分到这个子频带上.
就像跑道之间还要有一条隔离线作为隔离区域对不

FDM看起来非常好, 又公平, 还充分利用了信道带宽对吧. 但它有个非常重要的缺点:
FDM技术只能用于模拟信号的传输 , 因为一般而言, 只有模拟信号才有 频率 这个概念.

3.5.1.4 波分复用

概念: 波分复用(Wavelength Division Multiplexing, WDM)
将信道按照传输光信号的 波长 来分组. 本质上与频分复用是一个思路.

波分复用主要用于 光纤 .

上面我们提的方式挺完善 吗 ?
要知道互联网不仅仅是一对一, 而经常涉及到一对多的通信. 上面这些方式, 如果要进行一对多的通信, 会显得非常繁琐不是吗?

因此, 码分复用出现了.

3.5.1.5 码分复用

概念: 码分复用(Code Division Multiplexing, CDM)
各个节点预先获得自己的 码片序列 , 并根据自己的码片序列向接收方传送数据, 接收方能够根据传送数据的特点判断出是属于哪个发送方的.

哎, 这里有个玩意叫 码片序列 , 读者可以把它考虑为一个 多维向量 , 并且这个向量的每个分量都取1 / -1 .
举个例子, 下面就是几个码片序列:

$$ \vec{a} = (1, 1, 1, 1) $$

$$ \vec{b} = (1, -1, 1, -1) $$

通常而言, 发送方会发送 $ \vec{sender} $ 来表示1, 发送 $ - \vec{sender} $ 来表示0 .

注意: 码片序列的正交性
为了让接收方更好的区分不同的发送方, 通常而言, 码片序列之间被规定为 严格正交(即相乘得0) .

好的, 我们现在搞明白了发送方怎么发数据, 那接收方怎么收数据?

这里涉及到一个数学方面的运算, 被称为 规格化内积 .

假设发送方a发了个比特1, b发了个比特0.
接收方应当接收到这两个比特的加和, 即 $ \vec{a} + (- \vec{b}) $ .
此时发送方干这么一件事: 分别用 $ \frac{1}{向量维数} $ 以及 $ \vec{sender_i} $ , 乘上它拿到的这个叠加向量, 即:

$$
\begin{align*}
\frac{1}{m} \space \vec{a} * (\vec{a} + (- \vec{b})) \\
\frac{1}{m} \space \vec{b} * (\vec{a} + (- \vec{b})) \\
\end{align*}
$$

哎嘿, 挺神奇, 是不是上面得1, 下面得-1;
正好对应a发送1, b发送0.

通过这种方式, 能够使不同的发送方同时发送数据, 而接收方能够分辨出每一部分数据的来源. 但代价是数据包的大幅度膨胀.

3.5.2 随机访问介质访问控制

啥是 随机访问介质 ?

概念: 随机访问介质
意味着个个节点能够随机的去访问的信道介质. 是访问介质的一种全新控制思路.

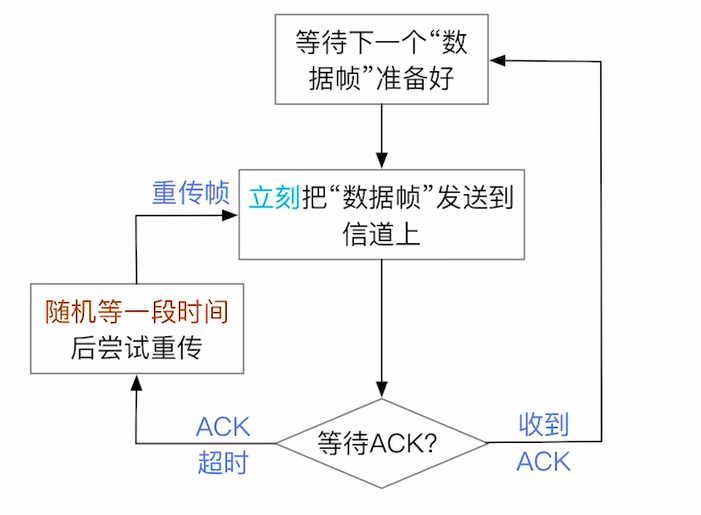
3.5.2.1 纯ALOHA

ALOHA最开始是夏威夷的一帮人搞出来的, 为了联通整个夏威夷的网络. 但后续因为思路值得借鉴, 传下来了.

其发送思路非常简单粗暴, 直接上图:

注意
ALOHA的重要特征如下:

1. 未收到ACK, 会 随机等待一段时间再重传 .
2. 可以在 任意时刻 将帧发送到信道上.

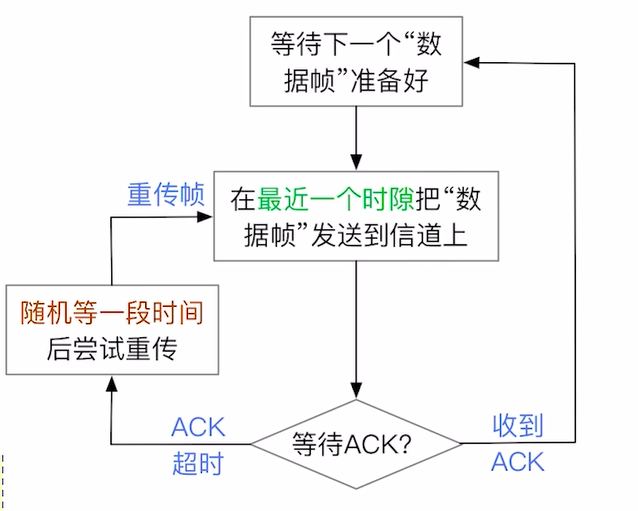
3.5.2.2 时隙ALOHA

相比于ALOHA增添了关于 帧上传的部分要求 .

注意
时隙ALOHA的重要特征如下:

1. 同样在传输失败后 随机等待一段时间
2. 规定时隙, 每个节点只能在一个时隙开始的时间点将数据帧发送到信道上

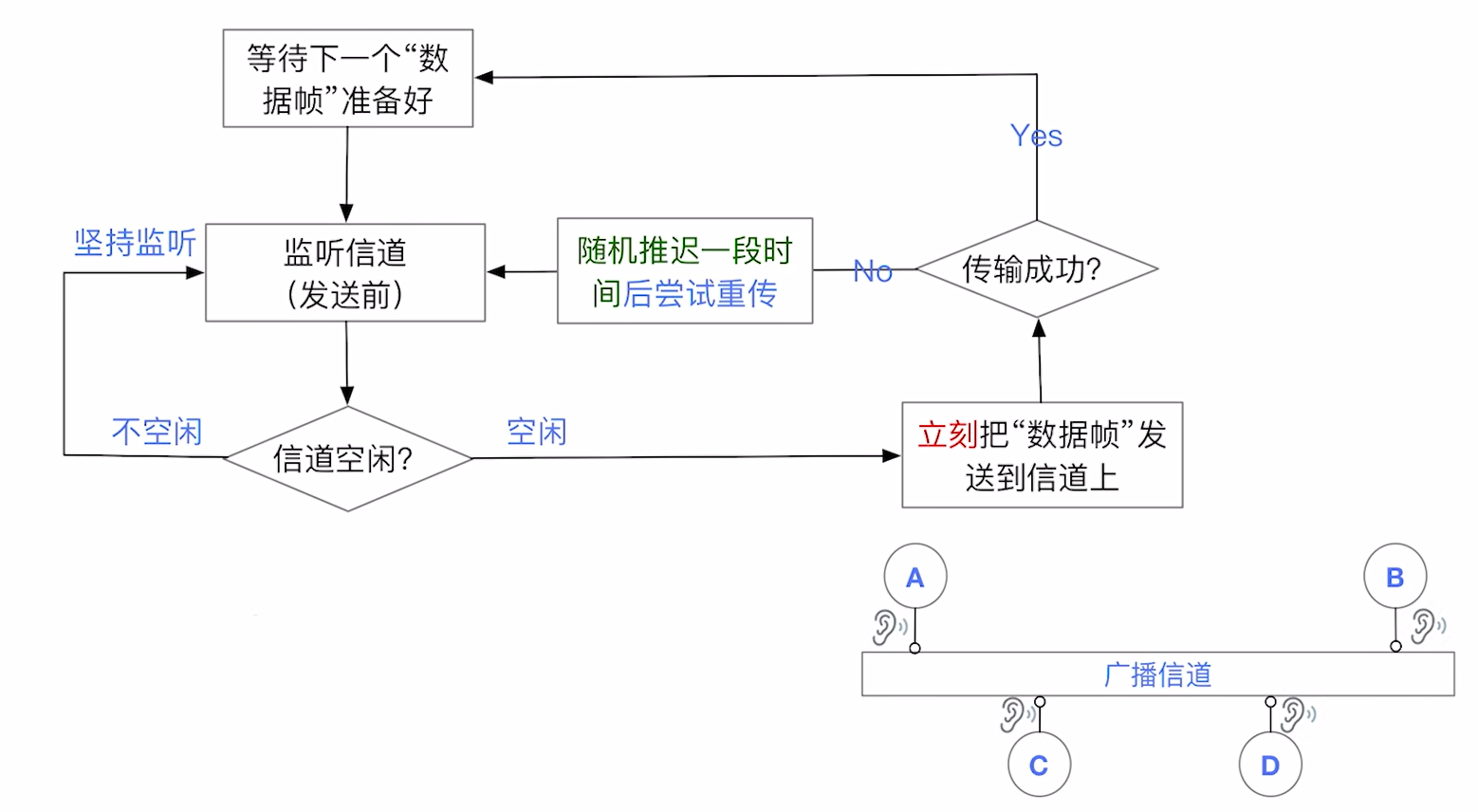
3.5.2.3 CSMA

CSMA是 Carrier Sense Multiple Access 的缩写, 中文译名为 载波监听多路协议 . 它首次引入了 监听 这一概念.
简而言之, 就是节点在发送数据前会先监听信道是否空闲, 只有满足空闲前提, 节点才会开始传输帧.

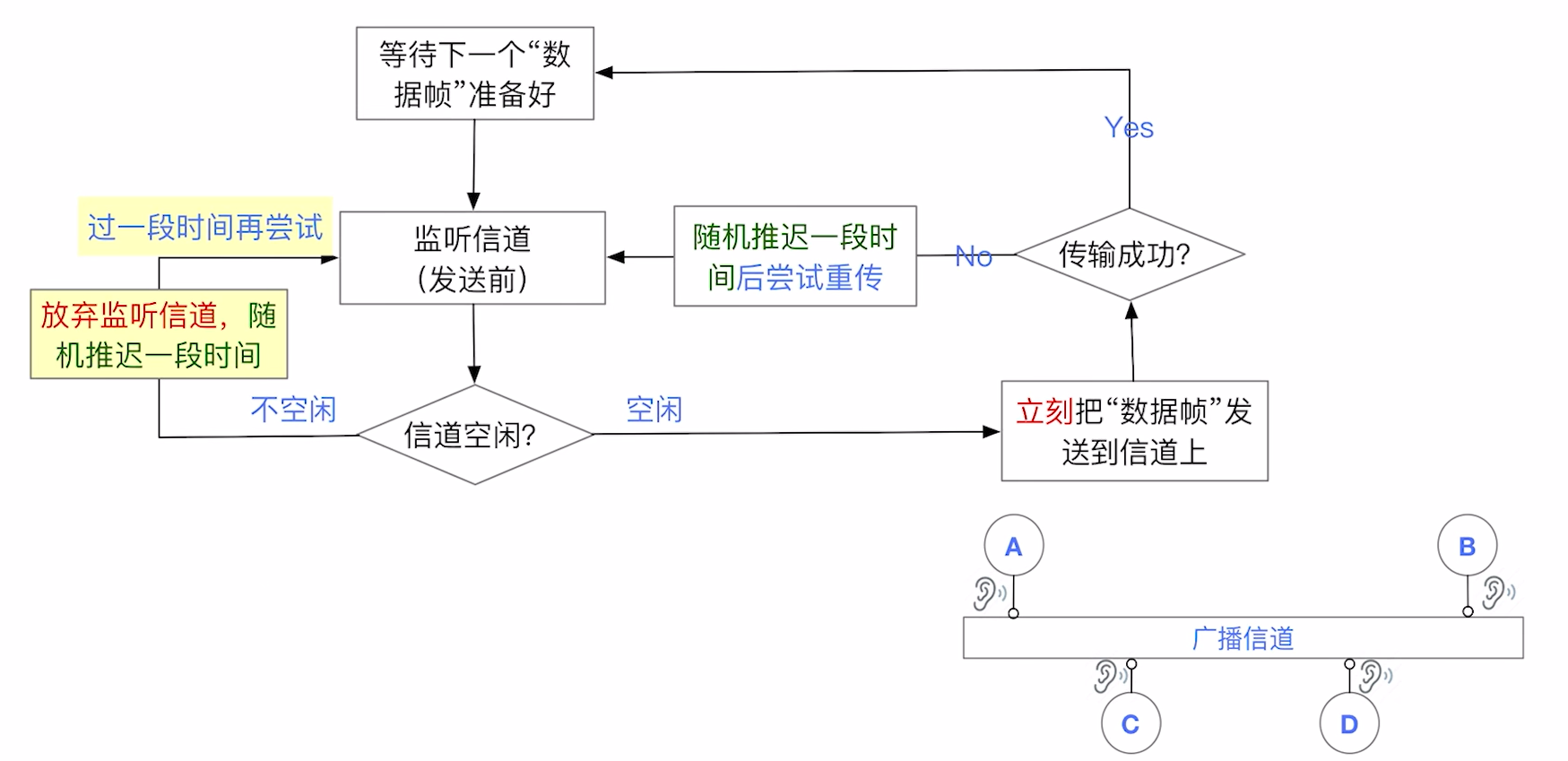
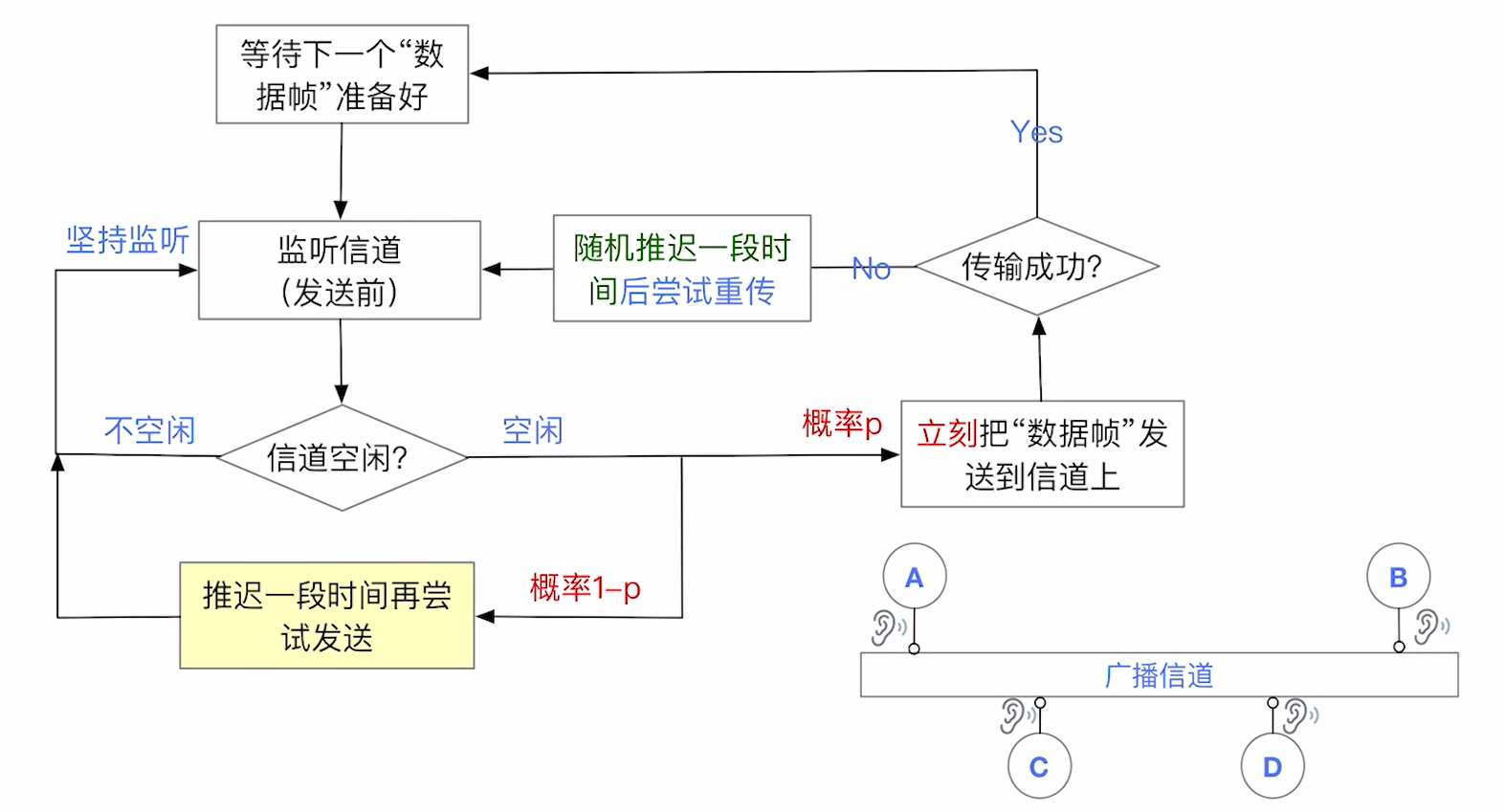
CSMA又有:

• 1-坚持 : 一旦我想发送数据帧, 我就一直看着这个信道, 直到空闲为止
• 非坚持 : 如果信道现在有人, 我就先屯着不发, 过一段时间再来看看
• p坚持 : 我会一直看着这个信道, 但是我 有概率 不立刻传送我这个数据帧

还望读者通过这三张图能够明确这仨协议的区别.

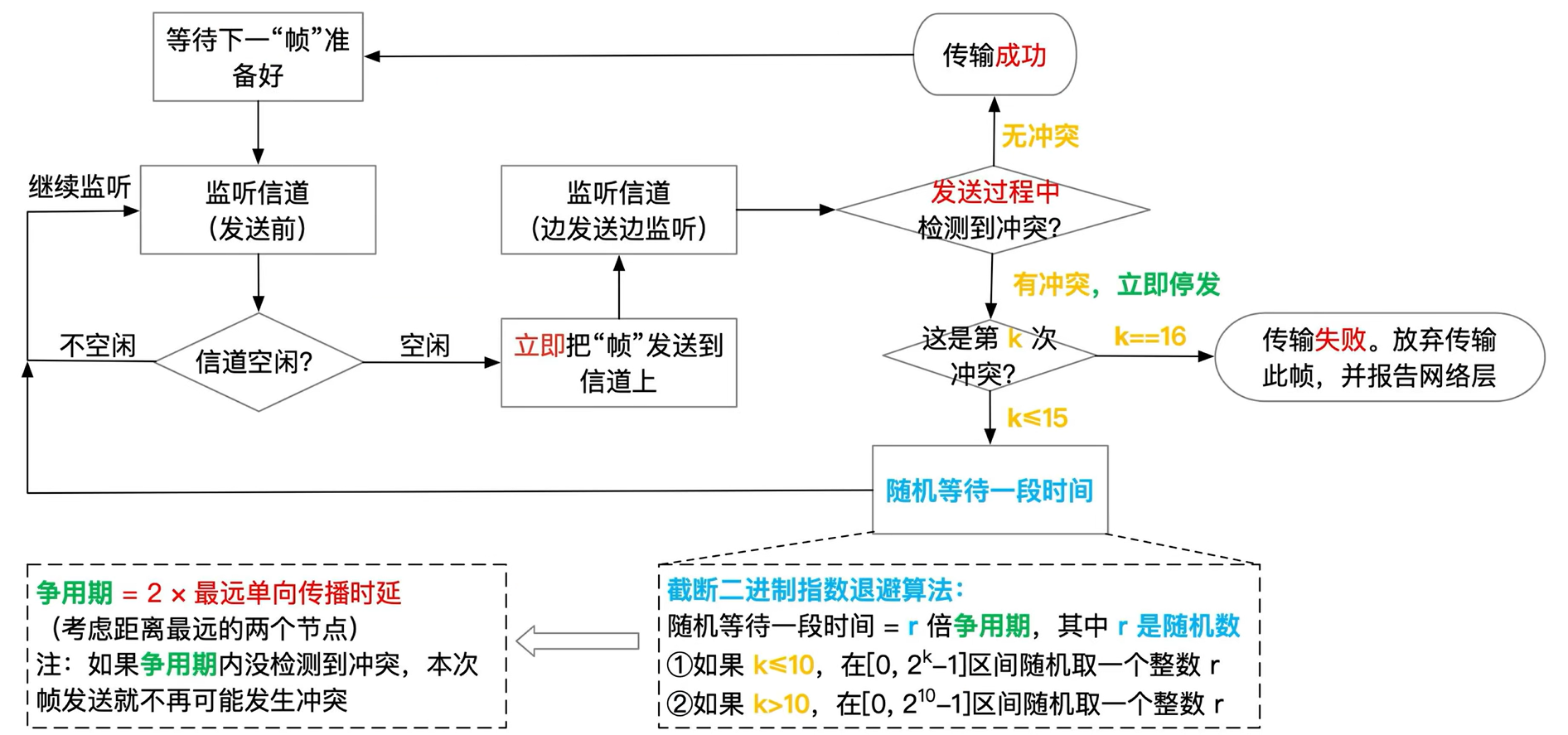
3.5.2.4 CSMA/CD

这个协议用于早期的 有线以太网 . 跟我们上面说的 1-坚持CSMA协议 比较类似.

CSMA的缩写我们上面提过了, 主要就是一个 监听 . 这里后面的CD是 Collision Detection 的缩写, 即 冲突检测 .
咸鱼给出了一段很简单的总结: 先听后发, 边听边发, 冲突停发, 随机重发 .

注意
CSMA/CD的重要特征如下:

1. 与 1-坚持CSMA 类似, 会一直盯着信道的当前状态. 并在空闲时立刻上传手中的帧.
2. 具备冲突检测功能, 当检测到冲突后(冲突次数为第k次), 会根据冲突次数做出抉择:
   2.1) 当前冲突已经是第16次了, 直接放弃传输该帧, 这往往代表着网络过于忙碌
   2.2) 当前冲突在15次即以内, 则挑选一个合适的随机时间进行数据帧的重新发送任务.

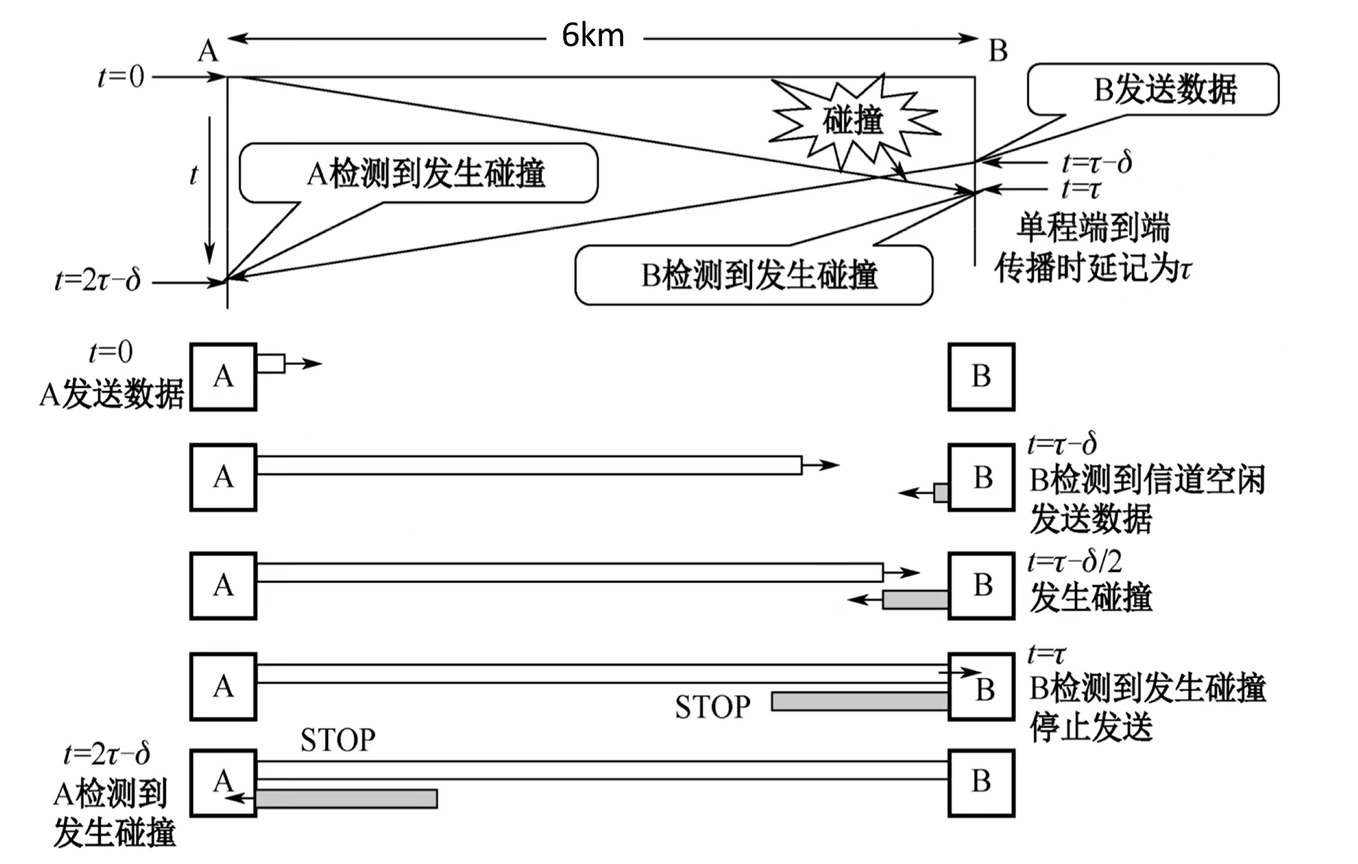
这个随机时间怎么挑选: 肯定是一个 争用期 的整数倍.

概念: 争用期
两倍的最远单向传播时延, 即距离最远的两个节点的传播时延.

• 如果冲突次数在10次及以内: 挑选 $ random(0, 2^k-1) $ 倍的争用期
• 如果冲突次数在11~15次之间: 挑选 $ random(0, 2^{10}-1) $ 倍的争用期

这里我们对 争用期 这个概念作进一步说明.

由于争用期是两倍的最远单向传播时延, 为什么是两倍呢?
考虑以下这种情况, 信道最两端的两个节点 A, B需要传输帧, 此时A的帧比特马上就要到B的位置, 但B此时监听信道应当还是空闲的(因为A的数据还没到嘛).
恰好, B这时候准备好了一个帧, 直接发出去了.
会发生什么 ?

B一定很快就发现了数据冲突, 因为我们刚刚说A的数据马上就到了.
但A呢 ?
它需要再等到B的数据走过一个最远单向传播时延, 才能知道, 哦, 原来我费劲巴力传了这么久的一个玩意冲突了.

因此算上A的数据走到B处的一个最远单向传播时延, 这意味着A需要至少等一个争用期, 找不到冲突, 才代表着这个帧正确的发送完毕了.

我们刚刚说的是最极限的情况, 因此, 只要一个争用期内没有检测到冲突, 代表着 A的数据流已经占领了整个信道 , 也就意味着不会再出现冲突了.

考虑上图中 $ \delta \to 0 $ 的情况, 就是我们的描述.

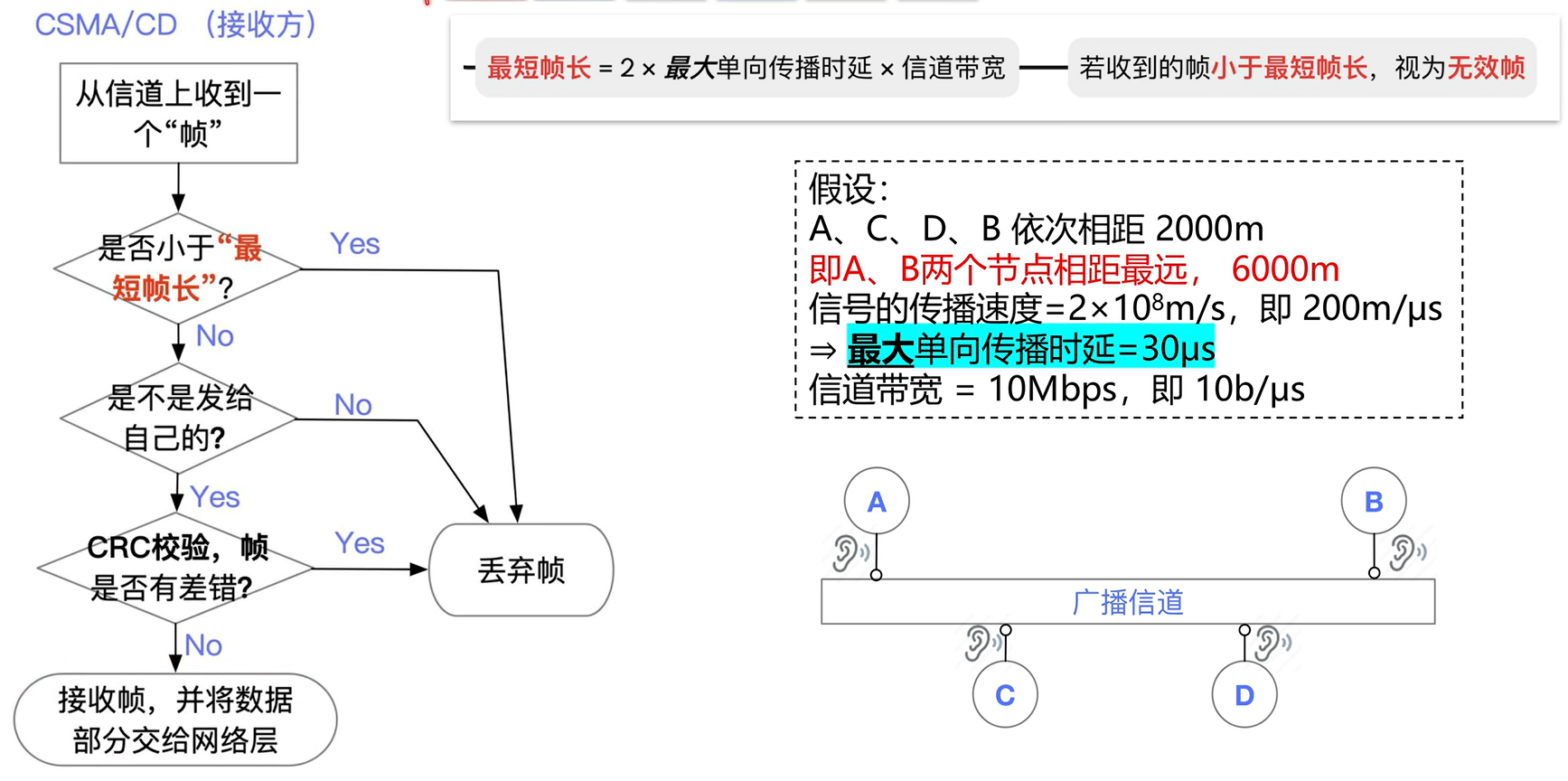
理解了 争用期 之后, 对于 最短帧长 这个东西应该就不难懂了.

CSMA/CD规定, 节点发送的最短帧不得短于: 2 * 最大单向传播时延 * 信道带宽 . 也就是 一个争用期内能发送的最大数据量 .

这很好理解, 如果发送的数据量小于这个值, 那考虑上面那个极端的冲突例子, B的数据到A时, A的帧已经传输完毕了, 就导致A 以为自己已经传输完了而没有出现冲突 , 导致通信的错误.

哦, 对了, 为了防止有些 老赖 构造一个超级长的帧来长期占用一整个信道, 还有一个 最长帧长 的限制.

注意
在以太网中, 最短帧长是64B, 最长是1518B.

再考虑一下 CSMA/CD 的接收方干的活:

至此, 这一个很麻烦但很常用的 CSMA/CD协议, 我们就聊完了.

3.5.2.5 CSMA/CA

我们说CSMA/CD通常用于有线网, 那无线网呢? 这就是CSMA/CA干的活了.
首先, 这个 CA 是 Collision Avoidance 的缩写, 用中文讲叫 冲突避免 . 这意味着这个协议不是在发送数据的过程中监听冲突, 而是要在发送前尽可能想办法避免冲突的发生.

在正式进入这个协议的介绍之前, 我们得先补个概念: Access Point(接入点) .

概念: 接入点
接入点(AP)是一种网络硬件设备, 它允许启用无线通信的设备连接到有线网络. 是无线网与有线网之间的中心枢纽.
另外, 我们称呼在不同的AP之间切换这个动作叫做 数据漫游 .

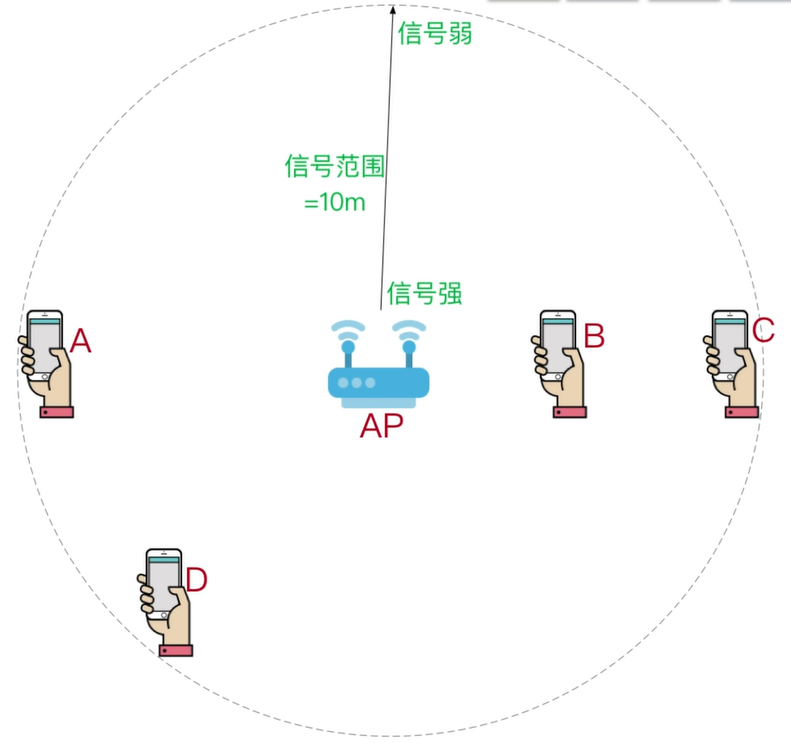
现在我们考虑为啥无线网不能用CSMA/CD?
考虑A发送数据的同时D也要发送数据, 此时, 不同于有线网的定向传输, 无线网中的设备是要向四面八方(也就是一个球体)发送信号的.
这会导致一种问题, 即A处接收到D的信号强度会远远小于A自身发出的信号的强度, 进而使得 冲突检测 这种行为的难度大大增加.
因此, 难办, 那不办了! 我们不检测, 转向一个 预测 的方向.

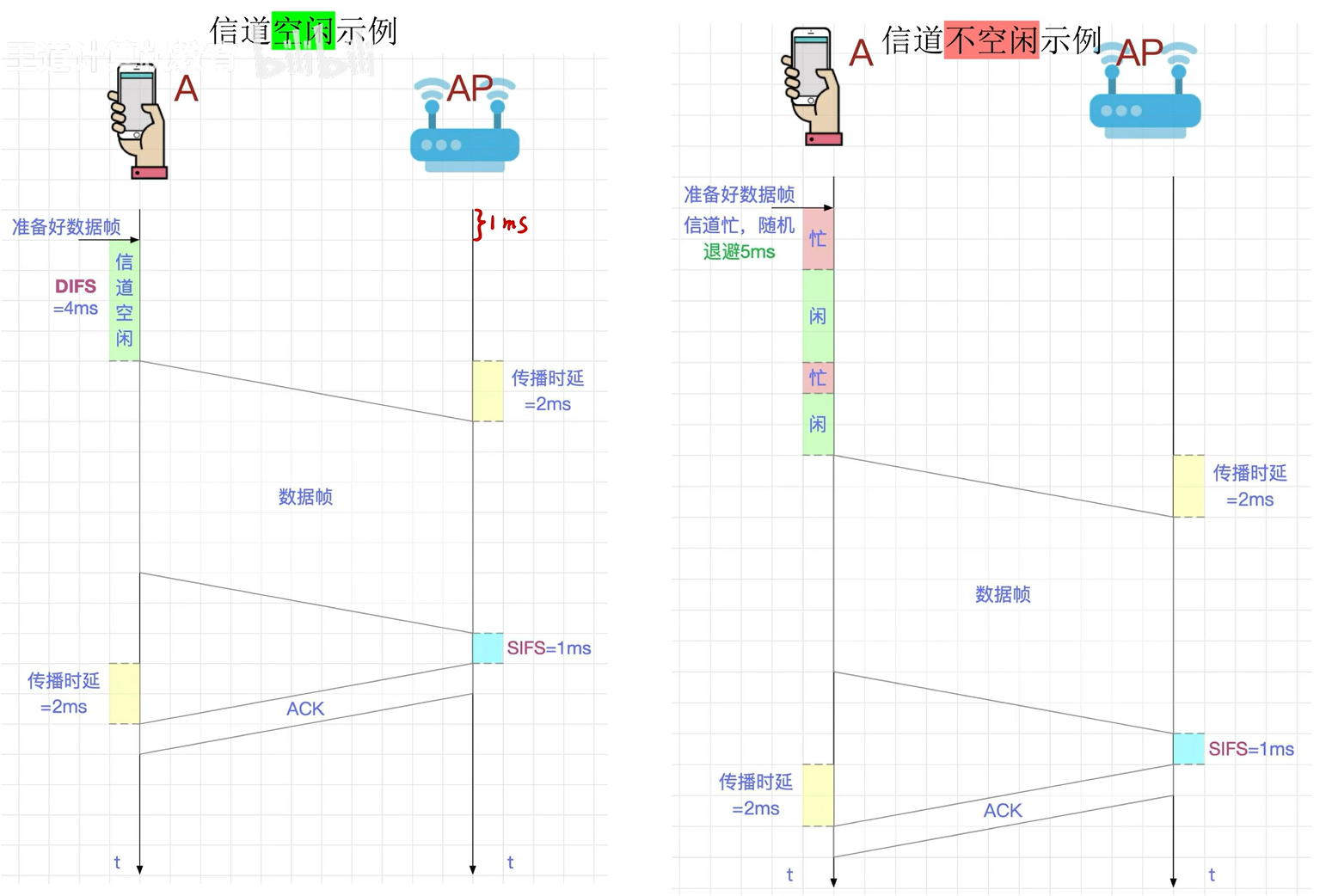
最简单的CSMA/CA是这样的:

其发送策略如下:

• 信道空闲
  • 发送方:
    • 准备好数据帧后检测信道, 如果信道此时空闲, 则等待一个 分布式协调IFS(DIFS) 的时间后发送整个数据帧.
    • 等待接收方ACK
      • 等到了, 进入下一个帧的传输
      • 等不到, 进行二进制指数随机退避, 随后尝试重传这个帧
  • 接收方:
    • 收到帧后, 在接下来一个 短IFS(SIFS) 的时间内立刻进行差错检测
      • 无错, 则返回ACK
      • 有错, 丢弃该帧
• 信道忙碌
  • 发送方
    • 准备好数据帧后检测信道, 如果信道此时忙碌, 则立刻进行二进制指数随机退避, 等待指定之间后直接传输该帧
    • 随后的事务与信道空闲情况下相同
  • 接收方
    • 与信道空闲情况下相同.

上卖弄涉及到了两个东西读者可能有疑惑:

• 帧间隔(Inter Frame Gap): 其实就是一段时间, 有长有短, 在IEEE 802.11标准中规定.
  • DIFS: 长帧间隔
  • SIFS: 短帧间隔
• 二进制指数退避算法: 跟CSMA/CD的退避算法几乎一致, 读者可移步该小节进行复习.
• 这里的接收方相当于采取了 停等协议 的收发策略.

我们这里再对这个DIFS简单说一下, 为啥这东西要最长呢?
通常有这么个公式:

$$ DIFS \geq SIFS + 最长传输时延 $$

这也是为了防止冲突的产生.

还是上图, 我们会发现再每个 SIFS 的时间内, 信道其实都是空闲的, 假如我们这时有另一个节点D, 不等待DIFS, 直接传输帧, 会发生什么?
可能这个帧就跟ACK撞上了对吧.

但如果我们发送之前都等待DIFS, 就能够检测到由于SIFS导致的信道状态延迟, 并采用退避算法.
显然这种方式比直接发送要更加智能一点.

读者可能注意到上面图片的名字叫 无隐藏站 , 这个隐藏站是个啥?
我们发现, 上面这种最简单的CSMA/CA全靠发送方来检测信道是否忙碌, 这可靠吗?

要知道, 发送方可并不处于AP的位置, 因此显然有可能, 有些信号AP是能收到的, 但发送方收不到, 比如最开始那张图, 发送方A和发送方C很有可能互相收不到对方的消息. 这种情况被我们称之为 隐藏站 .

很显然, 这种情况下需要AP的直接介入才能真正判断信道是否空闲对吧.

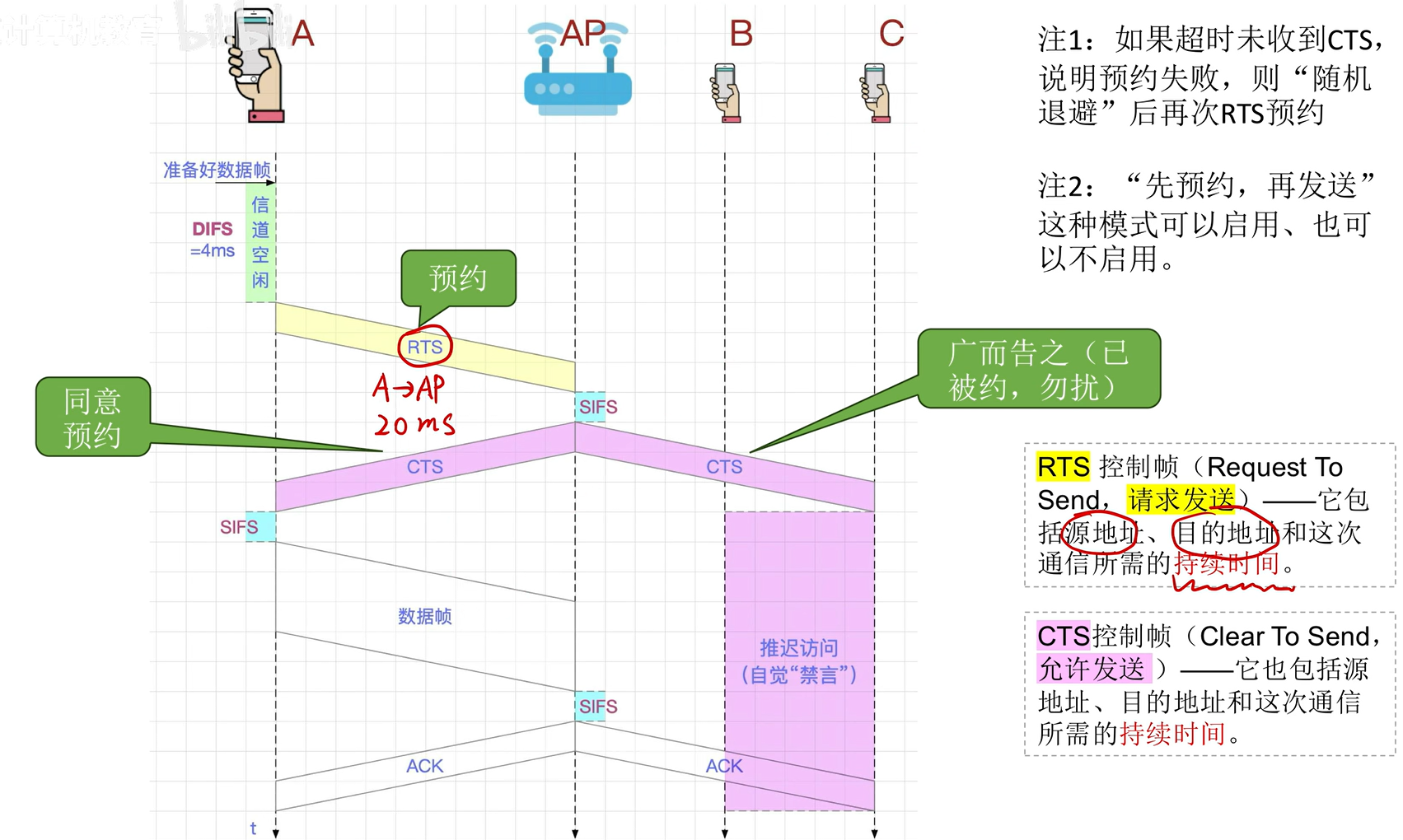
为了解决这个恼人的问题, 发明了个新的机制叫 预约机制 .

• 发送方:
  • 准备好数据帧后, 等待DIFS时间段之后向AP发送 RTS控制帧(Request to Send) , 该帧内需要包含预计发送时常, 等待AP的 CTS控制帧 .
  • 收到 CTS 后, 等待SIFS时间段, 随后开始传输数据帧
  • 如未收到 CTS , 立刻进行二进制指数退避, 并在此之后尝试重发 RTS .
• 接收方:
  • 收到 RTS 后
    • 若当前无其它预约, 则群发 CTS控制帧(Clear to Send) , 该帧内需要包含预约方和预约时长, 向所有节点明确当前的预约状况.
    • 若当前有预约, 则忽略该 RTS .

3.5.3 轮询访问介质访问控制

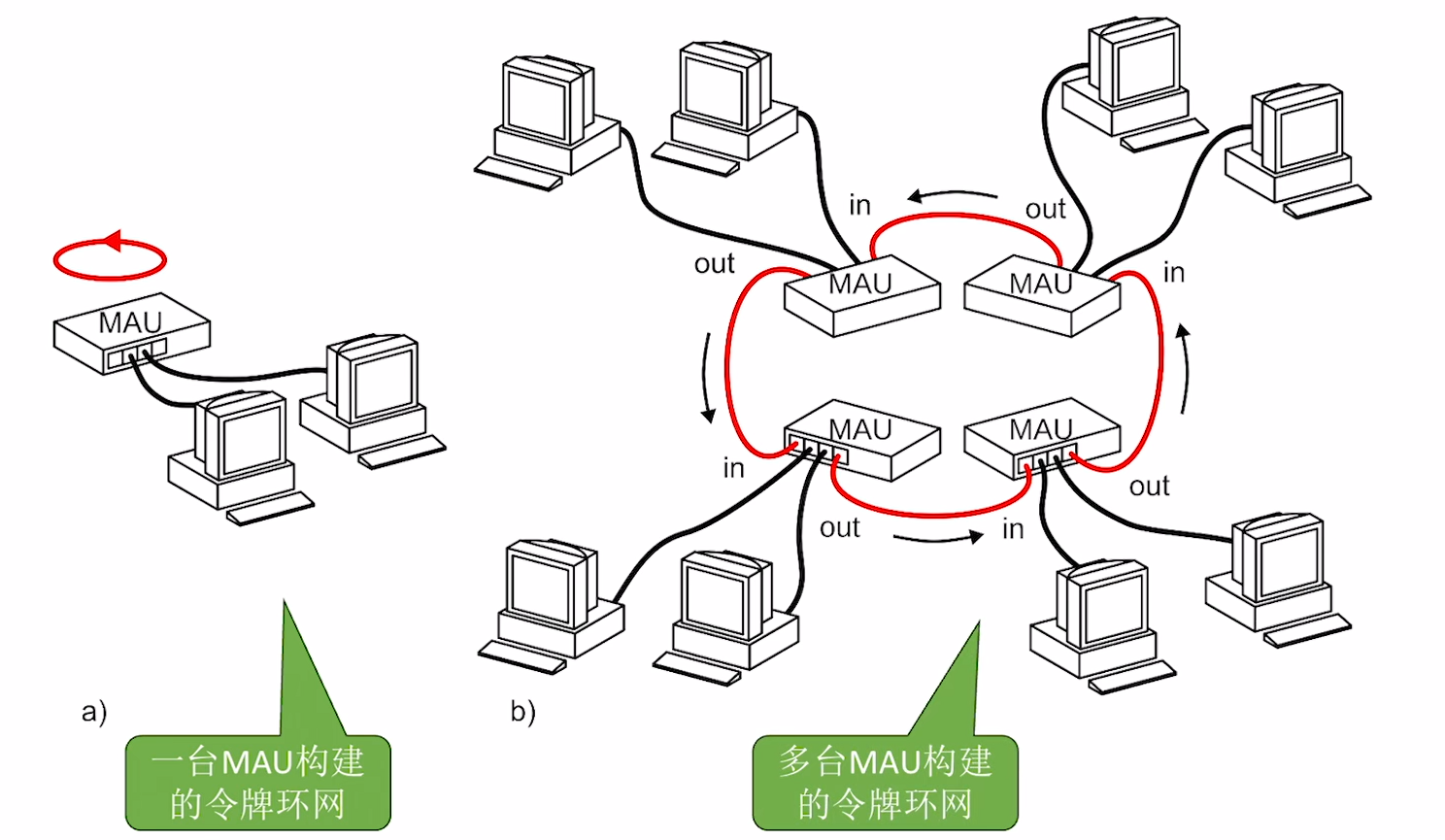
接下来是比较简单的轮询访问, 这种方式我们只说一种最简单的: 令牌传递协议 .

由于令牌传递的技术背景是IBM公司研发出的令牌环网, 但由于以太网现在已经极度成熟, 令牌环网已经逐步退出历史舞台, 因此这一节其实不是很重要.

这种方式的构想即整个网络中存在一个 令牌帧 , 而整个网络中只有持有这个令牌帧的节点才能够发送数据帧.
当这个数据帧发送完成并确定被成功接收后, 节点必须立刻放弃令牌帧的控制权并将其传输给下一个节点.
当然, 如果这个节点当前没有帧需要传输, 则立刻放弃令牌控制权.

通过这种传递方式, 使得整个网络不会出现数据冲突的情况.

还需要提一下, 令牌环网以及令牌传递协议需要一个叫 MAU(Multistation Access Units / 多站接入单元) 的玩意进行控制.

3.6 局域网

接下来我们了解的是当前世界上局域网的公认标准, 它是由IEEE这个组织的下属802工作组推行的.

3.6.1 IEEE 802 与局域网

我们上面说了很多种技术, 其大部分是通过企业发明的, 而后只有后续得到广泛认可的协议才能被IEEE重视, 成立下属工作组并指定国际标准, 比较著名的工作组包括:

• 802.8: 负责FDDI光线分布数字接口(已解散)
• 802.5: 负责令牌环网技术(已解散)
• 802.3: 负责以太网技术
• 802.11: 负责Wi-Fi技术

事实上, IEEE的覆盖范围远不止于此, 但由于我们计网的课程的研究范围大致为局域网内, 因此以下我们仅对部分局域网的知识进行讨论.

3.6.2 局域网的基本概念与体系结构

先给出局域网的基本特点:

• 覆盖较小的地理范围
• 具有较低的时延和误码率
• 以 帧 为单位在各个节点之间进行传播
• 支持 单播, 广播, 多播
  • 单播: 一对一发送帧
  • 广播: 对全部网内节点进行发送帧
  • 多播: 对某一部分指定节点进行发送帧

在IEEE的体系下, 当代局域网分为两个大类:

• 有限局域网(LAN)
  • 令牌环网
    • 时期: 1984 ~ 2000
    • 拓扑结构: 环形
    • 物理介质: 同轴电缆 / 双绞线
    • 采用协议: 令牌传递协议
  • 以太网
    • 时期: 1980 至今
    • 分类:
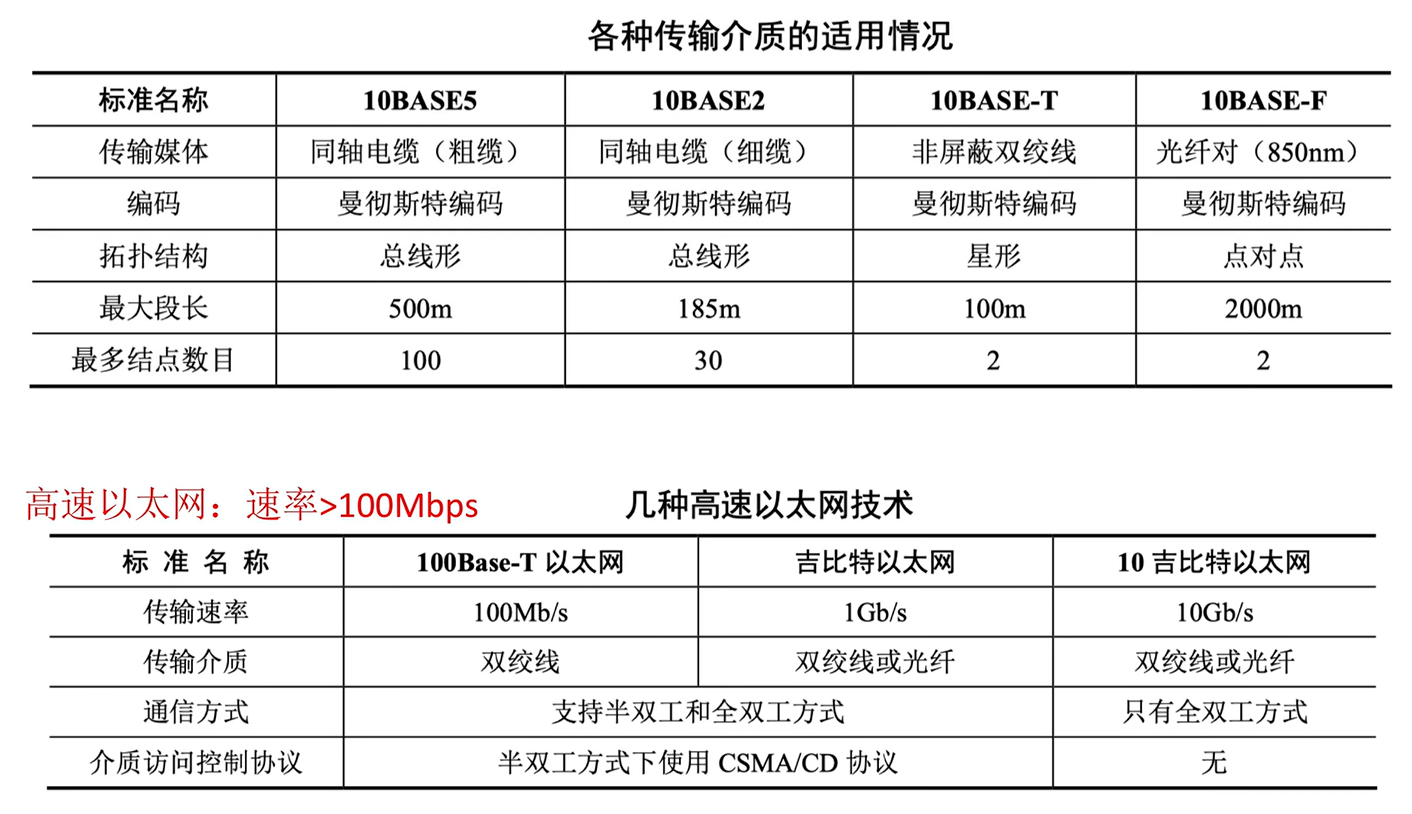
      • 同轴电缆以太网 (10Base5)
        • 拓扑结构: 总线型
        • 物理介质: 同轴电缆
        • 采用协议: CSMA/CD
      • 光纤以太网 (10BaseF)
        • 拓扑结构: 点对点 (因为光纤通常用于连接中间节点, 而不直接接入终端节点)
        • 物理介质: 光纤(两条, 全双工)
        • 采用协议: NULL, 不需要协议配合(因为是点对点, 不存在介质争用)
      • 双绞线以太网 (10BaseT)
        • 物理介质: 双绞线
        • 分类:
          • 集线器双绞线以太网
            • 拓扑结构: 物理上星型, 逻辑上总线型
            • 使用协议: CSMA/CD
          • 交换机双绞线以太网
            • 拓扑结构: 星型
            • 使用协议: CSMA/CD(半双工), 也可能是NULL(全双工)
• 无线局域网(WLAN)
  • Wifi 802.11
    • 拓扑结构: 星型(一台AP + N台移动设备)
    • 物理介质: 无线(Wireless)
    • 采用协议: CSMA/CA

ok, 这个表还是挺大的, 但是其实里面的知识我们之前都聊过.

这之后, 我们来看看直接跟数据链路层相关的 网络适配器 .

对于不同的链接方式(有限局域网 / 无线局域网), 设备中会配备不同的网络适配器.
一个网络适配器中有至少有一个ROM芯片, 它负责存储一个全球唯一的地址(MAC) , 来保证在局域网内发送给你的帧能够正确的找到你而不是别人.
这个MAC地址总共48位, 前24位由IEEE分配, 而后24位归网卡的硬件厂商来分配.

除此之外, 还会存在一个RAM用于暂存收到的数据帧(作为缓冲区).

注意
读者务必注意, 有线局域网和无线局域网的网络适配器不能共用, 这意味着如果你的电脑能接网线, 也能连Wifi, 则它必定有两个网络适配器, 而这两个适配器的MAC也一定是不一样的.
感兴趣的读者可以上网搜一下如何查看自己的网络适配器MAC地址. 这里笔者不赘述了.

总结一下网络适配器的功能:

• 把帧发送到局域网
• 从局域网接收帧
• 根据接入的局域网类型实现数据链路层和物理层的功能
• 支持帧缓冲机制
• 将IP数据报封装成帧 (有些是适配器干的, 有些是主机干的)

3.6.3 IEEE 802.3 有线局域网

接下来, 我们来看看有线局域网的具体内容.

IEEE 对于局域网主要探讨两部分的标准, 即物理层与数据链路层(MAC)的标准设定.
我们先看物理层. 直接上一张表:

这里需要注意的是关于物理介质对于双工模式的支持:

• 同轴电缆只能半双工
• 双绞线:
  • 速率 $ < 2.5Gbps $ 一般同时支持半双工 / 全双工
  • 速率 $ \geq 2.5Gbps $ 仅支持全双工
• 光纤只能全双工

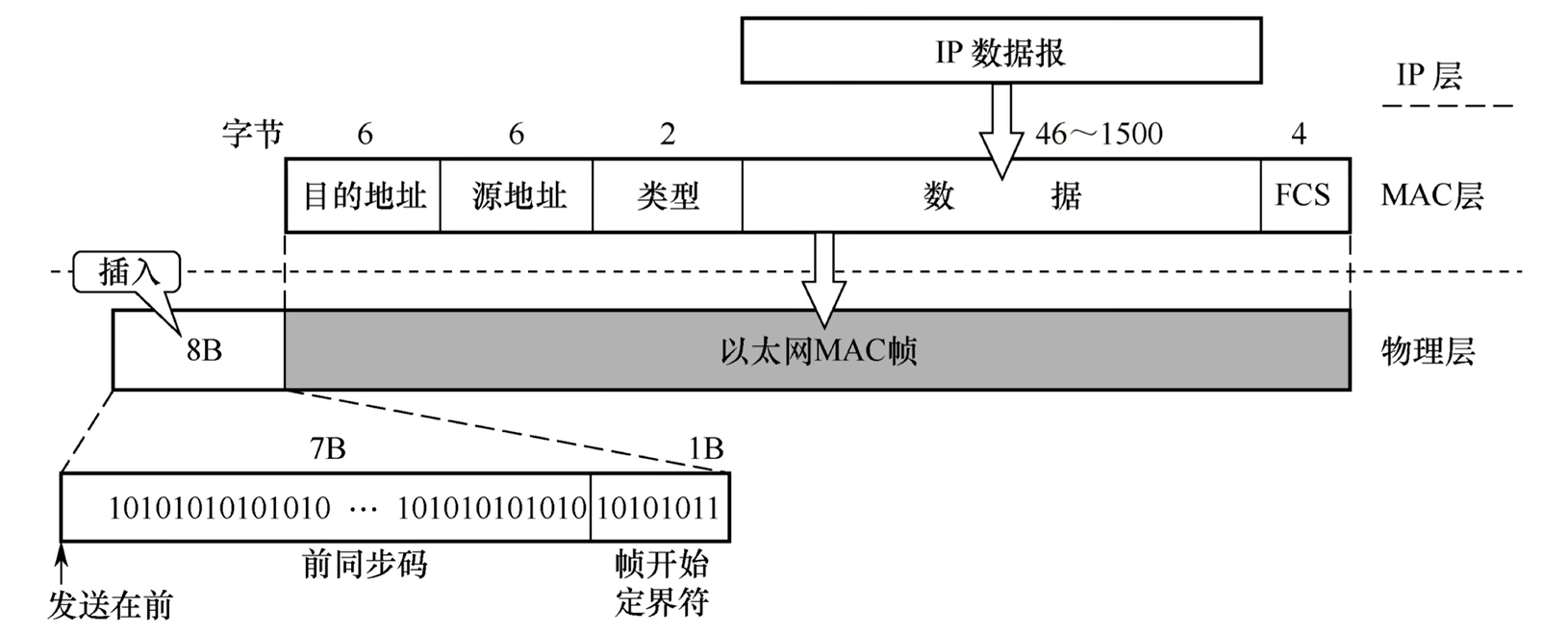
接下来看看数据链路层, 这一层的标准制定主要集中在 帧的结构 这一部分上, 这一部分当前主要有两种规定:

• DIX Ethernet V2
• IEEE 802.3

这两种帧的格式几乎一致, 并且前者目前是主流.

• 目的地址 / 源地址: MAC地址, 48bit(6bytes)
  • 目的地址如果全1, 则代表这是一个 广播帧 .
• 类型: 指明网络层使用的协议类型
• 数据:
  • 就是网络层的IP数据报 / ARP报文等玩意, 详见下一章.
  • 长度在46 ~ 1500byte之间(这里需要读者回顾一下为什么需要划定最短和最长帧长)
• FCS: CRC校验码

在物理层, 还会在一个MAC帧前插入俩玩意:

• 前同步码: 打节奏, 告知对方准备开始传输
• 帧开始定界符: 告知对方帧起始位置

这一部分读者可以回到Chap.2 进行回顾, 采用的是曼彻斯特编码(跳0反跳1, 中必变).

关于 广播帧 , 我们得稍微说一下.

对于一个广播帧, 交换机和集线器都会将其转发到自己连接的所有端口, 但 路由器不会 .
因此, 一个最底层的路由器的一个端口能够组成一个 广播域 , 广播帧只能传输给所在广播域的所有节点.

在这里, 还请读者进一步复习一下之前提到的 冲突域 的概念, 对这二者的区别做一个明确的认知.

3.6.4 VLAN基本概念与原理

VLAN(Virtual LAN), 是IEEE 802.1Q 工作组提出的概念. 目的在于在一个过大的广播域内对节点进行分组, 增加安全性, 并防止广播风暴的发生.

其思路很简单, 就是在通过交换机连接的某一个广播域内, 为不同的终端机进行分组, 从而形成一个个更小的 虚拟局域网 .
相应的, 一个虚拟局域网也对应着一个 VID .

VLAN的划分方式主要有以下三种:

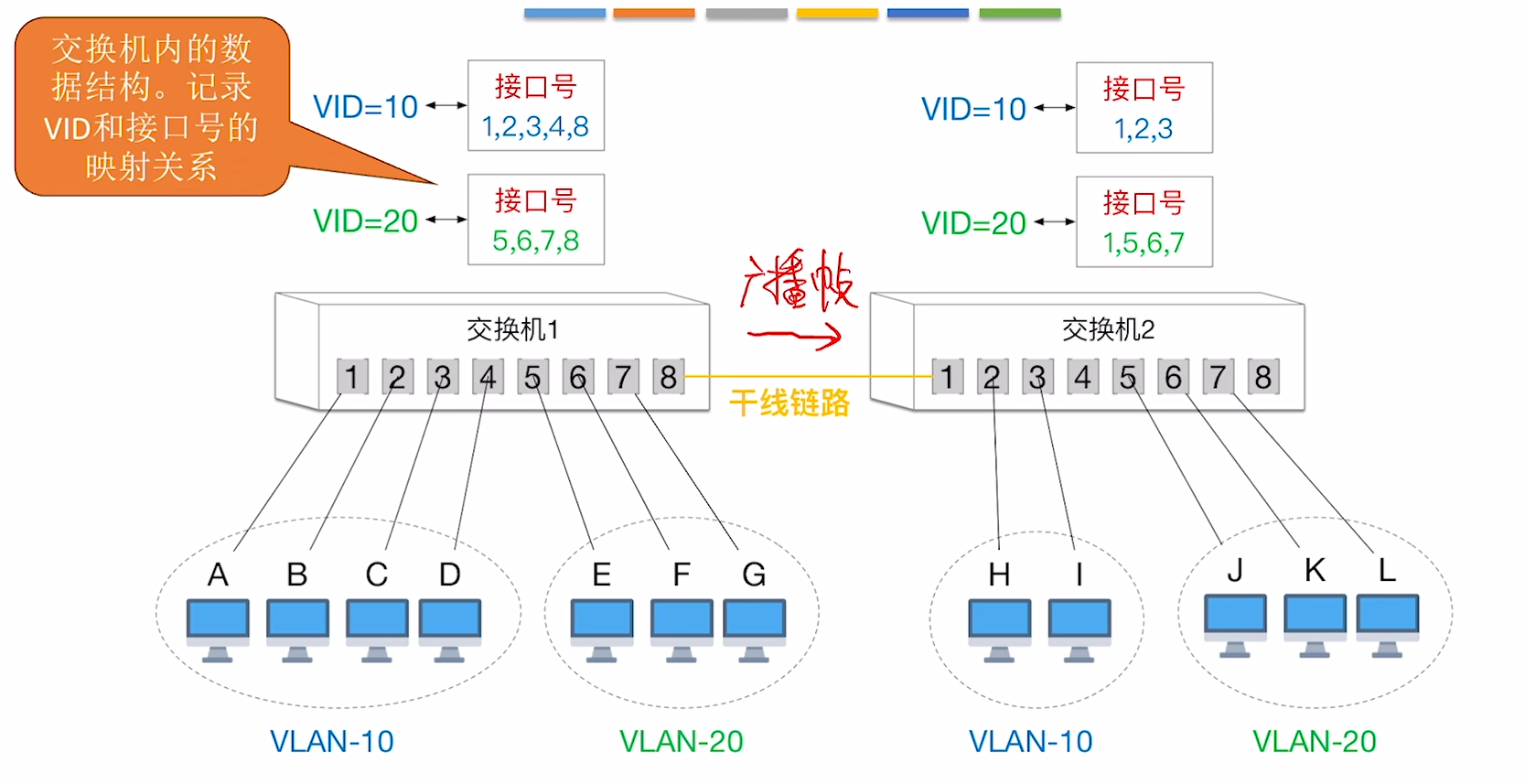
• 基于接口的VLAN划分: 按照交换机的接口来创建VID与接口号的映射.
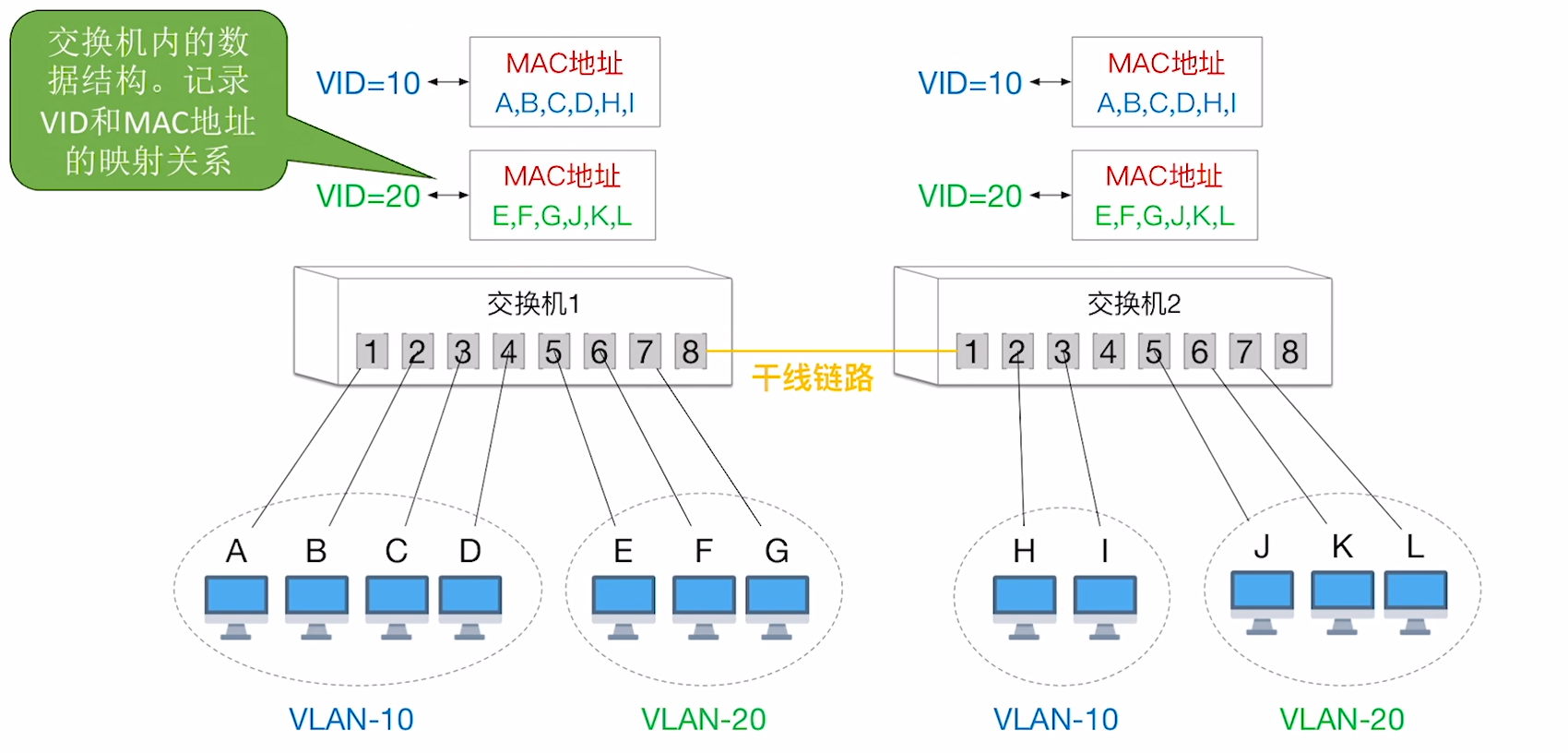
• 基于MAC地址的VLAN划分: 按照终端机的MAC地址来创建VID与地址的映射.
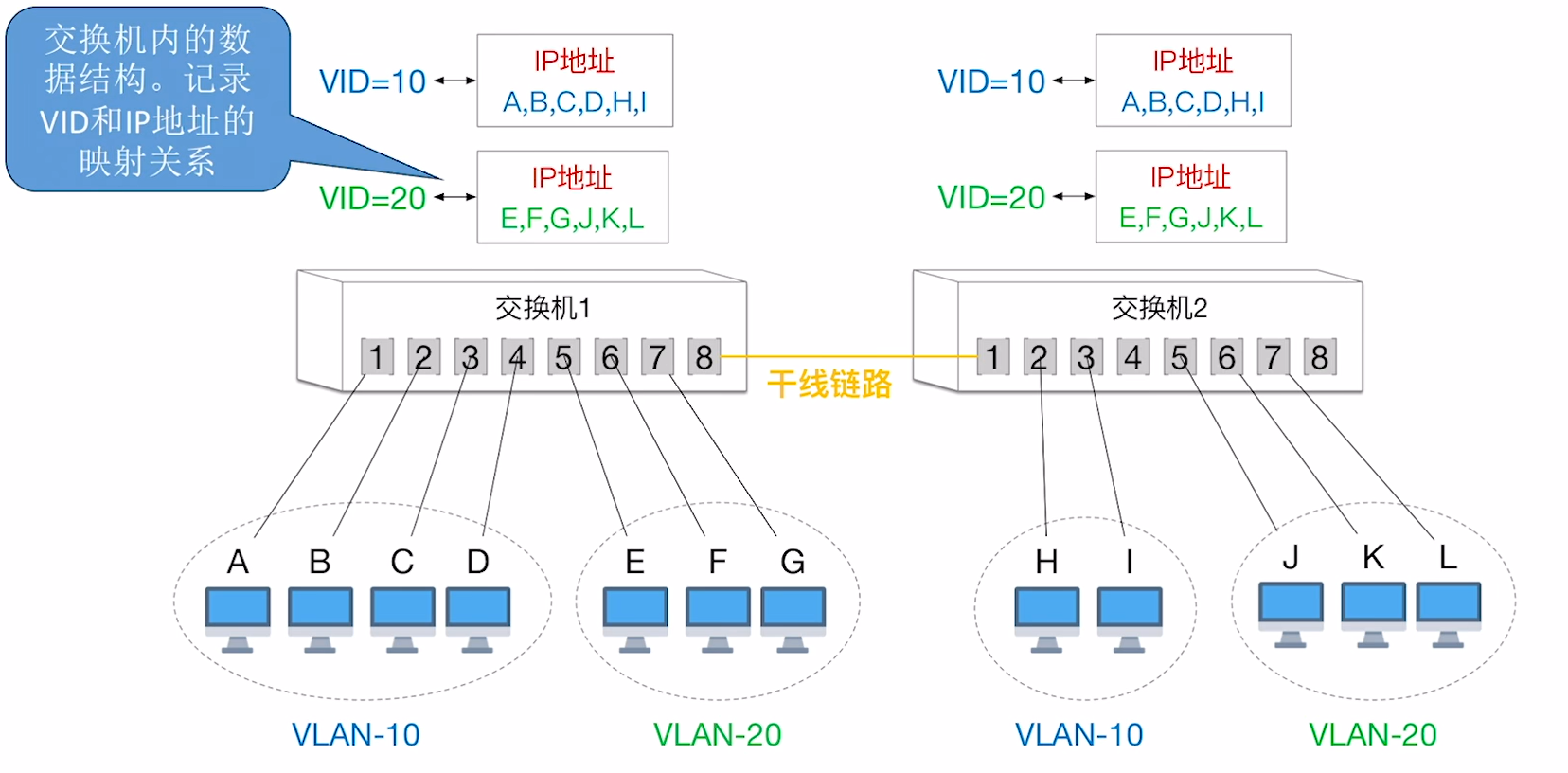
• 基于IP地址的VLAN划分: 按照终端机的IP地址来创建VID与地址的映射.

值得额外提一下的是, 由于IP是网络层的概念, 这种划分方式需要网络层设备的支持.
也相应的, 这种划分也能让VLAN达到 跨越路由器 的效果.

最后的问题是, 不同的交换机该怎么判断这个帧属于哪个VLAN呢? 我们之前说的标准以太网帧里面没有这东西.
那很简单, 没有就加上.
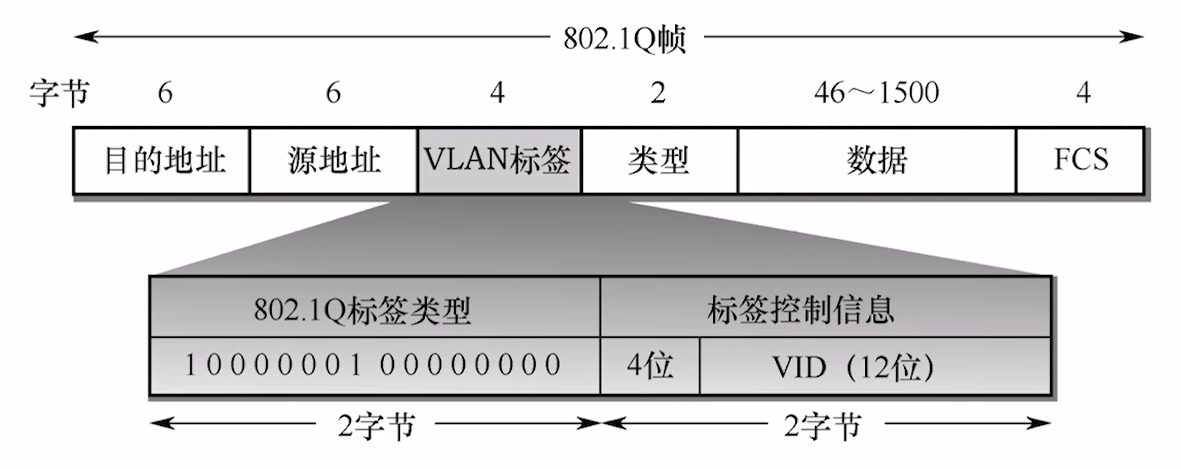
因此 802.1Q帧 诞生了, 它主要在不同的交换机之间进行通信.

相比于普通的以太网帧, 其单纯在帧内加了一个VLAN标签.

注意
由于802.1Q帧加了信息, 因此其末尾的FCS(CRC校验码)的部分需要再次生成, 这里不再赘述.

3.6.5 IEEE 无线局域网

这一部分主要了解一下无线局域网的部分内容.

首先, 无线局域网不仅仅只有Wifi奥, 按照官方的分类, 其分为以下两类:

• 有固定设施的无线局域网(即 IEEE 802.11 无线局域网 Wifi)
• 无固定基础设施移动自组织网络(AipDrop, 各厂商的Share等…)

由于第二种主要是各个厂商自行组织定义的, 因此我们的了解重点还是在第一种 802.11 上.

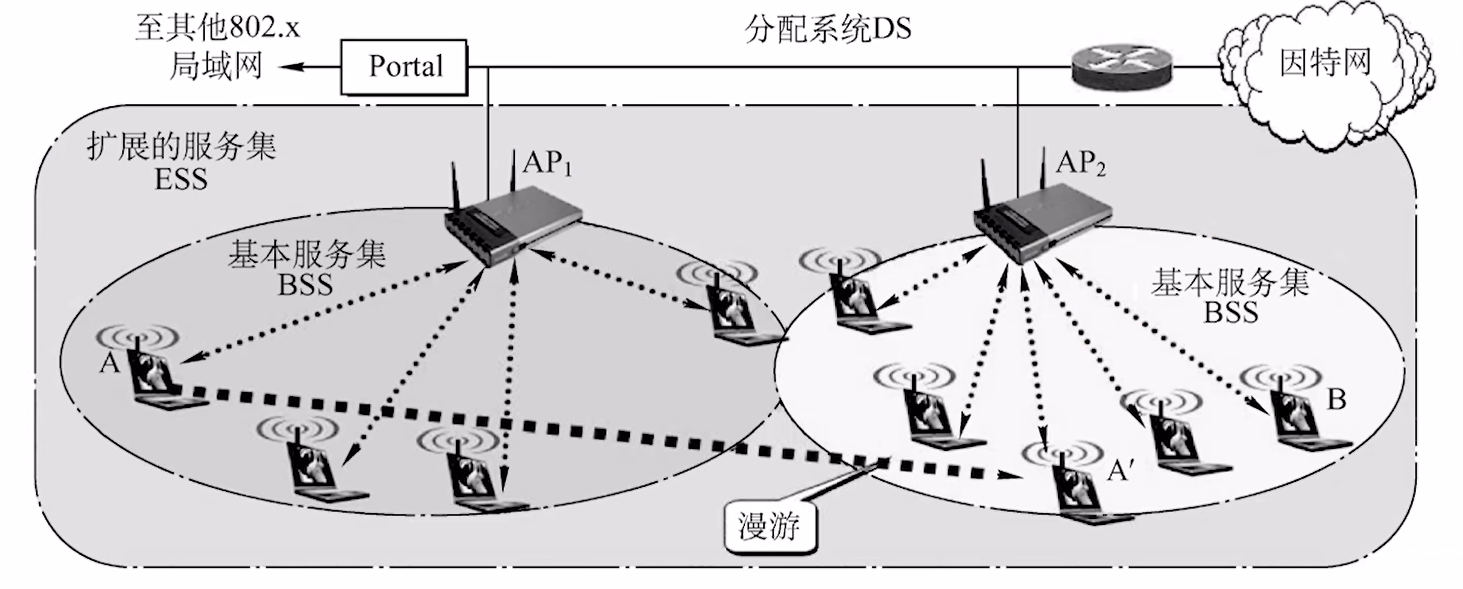
我们首先了解一下802.11无线局域网的一些概念与结构:

上面这个图有几个重要的概念, 它们是无线网能够建立的核心:

• Portal(门户): 相当于一个协议转换器, 能够将802.11的协议和802.3的协议互相转换, 使得无线网和有线网能够互通.
• AP(接入点): 之间我们说过, 就是一个无线网接入的中心节点. (说人话就是你家的路由器)
• 基本服务集(BSS): 一个接入点以及通过它连接上网的所有终端节点. (说人话就是路由器 + 连接的所有手机电脑)
  • 服务集合表示(SSID): 无线局域网的名字(标识符) (说人话就是你家的Wifi名)
  • 基本服务区(BSA): 一个基本服务集能够覆盖的地理范围 (说人话就是能搜到你家Wifi的范围)
• 漫游: 一个移动站在不同的服务集之间切换, 能够保持通信 (说人话就是你换了个Wifi, 还能上网)

可以看到802.11无线网跟有线网差的还挺大, 那自然其帧也不太一样.
具体而言, 802.11 分三类帧:

• 数据帧
• 控制帧: ACK, RTS, CTS(这里不熟悉返回至CSMA/CA协议)
• 管理帧:
  • 探测请求帧: 发给AP用于探测有哪些接入点(能搜到哪些Wifi)
  • 探测响应帧: AP发回给终端设备来表示自己可以接入(我这个Wifi可以被探测并连接)

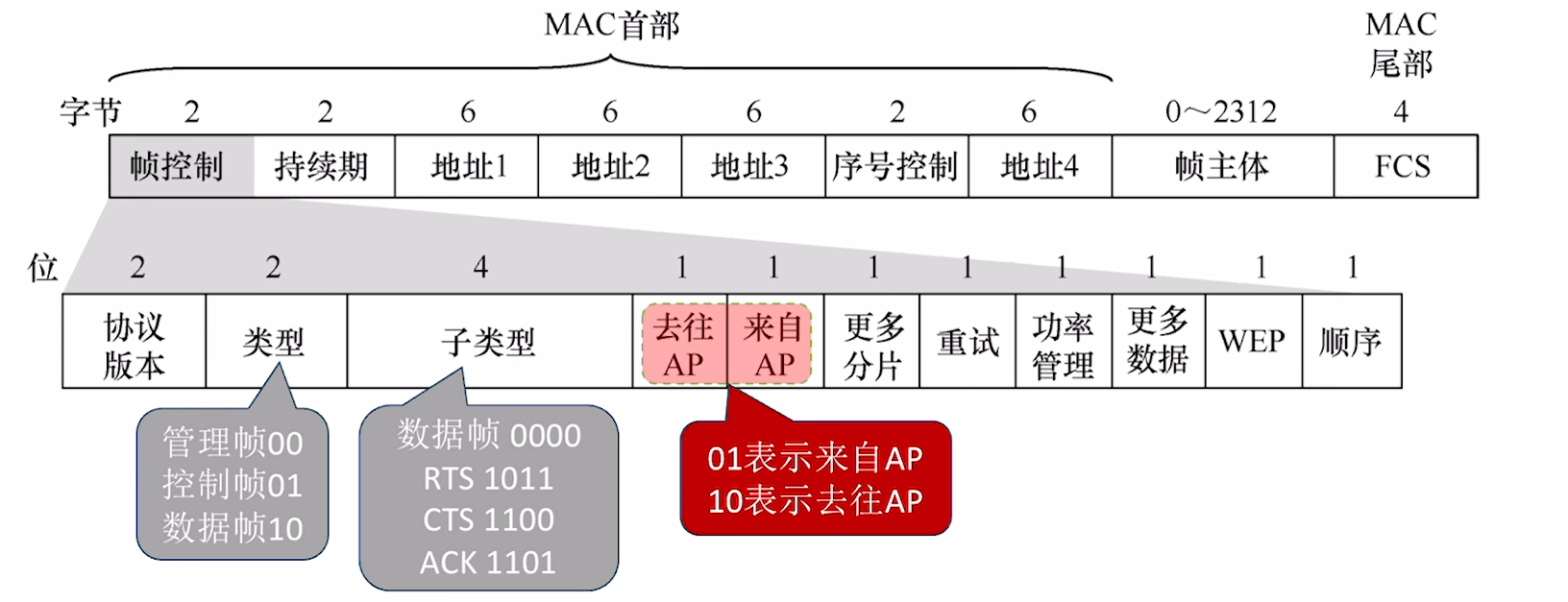
我们对这个帧进行一些说明:

• 类型: 管理 / 数据 / 控制
• 子类型: 每种帧下属的子类型
• 去往AP / 来自AP: 用于标识这个帧的发送方向
• 地址1
  • 去往AP: AP
  • 来自AP: 接收方
• 地址2
  • 去往AP: 发送方
  • 来自AP: AP
• 地址3
  • 去往AP: 接收方
  • 来自AP: 发送方

注意
在802.11中, 两个移动站不能直接通信, 必须通过AP进行转发通信.

3.7 以太网交换机

交换机之前提了挺多次, 但我们一直不知道这玩意到底是怎么实现 转发帧 这个功能的.

3.7.1 交换机的自学习功能(即插即用)

我们在说以太网帧的时候, 有这么一张图:

这张图上明确的有源地址和目的地址对吧.

交换机内部会自行维护一张表(MAC地址表), 其表项为 {MAC地址, 端口号} .
当其收到一个帧的时候, 干两件事:

• 将源地址的MAC与进入的接口进行映射, 建立表项.
• 会先将目的地址与当前所有表项进行对比, 如果能够找到该MAC, 则仅向对应的端口进行转发, 否则向所有的端口转发该帧.

现在就还有个问题, 因为MAC地址是跟接口绑定的, 那假如有节点换接口了咋整?
交换机里面的表项是有一个最长有效期的, 当超过这个有效期就会自动作废, 此时交换机就找不到这个表项了, 因此会再次向全部的端口转发这个帧.

3.7.2 交换机的转发方式

当前交换机有两种转发方式:

• 直通交换
  • 只接收帧的前6个字节(即目的地址) , 随后查表, 找不到就全部转发, 找到了就定点转发.
  • 转发时延比较低
  • 不支持协议转换, 速率匹配, 差错控制
• 存储交换
  • 存储整个帧, 不仅匹配目的地址, 同时进行差错控制等工作.
  • 可以进行速率匹配以及需要差错控制的线路, 可以协议转换
  • 转发时延比较高

至此, 第三章就完事了.

这一章的很多内容还是很重要的, 我们初步谈了谈一些很重要的协议, 并且给出了一些在之后的层次中也很重要的内容(差错控制, 可靠传输, 流控等)

本篇博文就到这里~