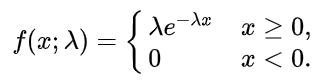区块链（Blockchain）

写在前面, 本文主要针对区块链的技术原理与实际应用进行说明.
当前, 区块链的技术主要应用领域仍然是加密货币, 因此不可避免地本文需要对加密货币进行一些相关的说明. 但本文完全不推荐, 或推崇无谓的挖矿行为, 烦请读者不要先入为主, 理性看待本文所描述的技术.

本文主要基于 《区块链技术与应用》(北京大学 肖臻教授) 的课程进行笔记整理与内容扩展, 文中除开视频内容外,也会涉及到一些博主自己的思考, 烦请读者理性看待. 在此也附上视频链接(https://www.bilibili.com/video/BV1Vt411X7JF?p=1&vd_source=4565edcb254cb6582d6382ac80011294), 有了他们的工作, 才能让区块链这一技术为更多人所知.

在此, 对 肖臻教授 以及 北京大学相应课程组 表达诚挚的敬意与感激!

Part1. 区块链是个啥？

引用一段来自维基百科的定义：

A blockchain is a distributed ledger with growing lists of records (blocks) that are securely linked together via cryptographic hashes.

根据这段定义我们可以得知，区块链这玩意其实就是一个账本，它可以通过哈希算法将一串东西连在一起，这也是它被称作“链”的原因。

更形象的一段话：

Each block contains a cryptographic hash of the previous block, a timestamp, and transaction data (generally represented as a Merkle tree, where data nodes are represented by leaves). Since each block contains information about the previous block, they effectively form a chain (compare linked list data structure), with each additional block linking to the ones before it.

意味着这玩意大小可变，后续增加进去的“块”会附带着前一个区块的信息（包括哈希值、时间戳、交易数据）。同时这个过程事实上是不可逆的：

once they are recorded, the data in any given block cannot be altered retroactively without altering all subsequent blocks.

同时，区块链往往和 Web3.0 联系紧密，即分布式互联网的思想。这意味着你只违规的修改自己手中的账本是无用的，因为它并没有被大众所认可，只有遵循相应的规则，才能够在所有拥有这个账本的人的文件中，添上一笔。

Part2. 密码学原理

上方引用的定义中，有一个词还挺引人注目的： Cryptographic hashes。

事实上，我们很容易想象到这个玩意的意义，要确定一个规则不易被攻破，则自然需要一个算法（也可称为密码算法），我们称呼这个密码学标准为： Cryptographic hash function ，即加密哈希函数。

2.1 哈希（Hash）

2.1.1 Collision Resistance

我们在排序的时候其实对哈希这个玩意做过一定的说明，这里引出一个哈希中比较重要的概念：“Collision Resistance” ，中文称为该哈希函数的抗碰撞性。哈希碰撞是一个哈希算法中常有的情况，即：给出了两个不同的输入x，y，而通过哈希函数算出的函数值H(x)，H(y) 却是相同的。很显然，我们需要尽可能降低这种情况发生的可能性。

注意：我们需要明确，哈希碰撞理论上是不可避免的，因为哈希函数的取值范围是人为框定的，而哈希函数的输入值（或者说自变量取值）可以趋近于无穷大。因此我们说的 “Collision Resistance” 要做到的是 没有一个非常高效的方法来人工制造哈希碰撞 ，这个概念其实还挺重要的。我们无法阻止攻击者采取暴力破解（Brute-force）的方式来破解哈希算法，我们能做到的是尽可能拉长他们需要花费的时间，使得它们破解这个哈希算法的行为在这个时间长度的影响下趋近于无意义。

哈希这个玩意的另一个作用在于可以保证一个文件（message，我们简称为M）不被篡改，因为这个M里面的值一旦被改了，其哈希函数值H(M)也必定会发生改变，这就被其他人所共知了。

但很遗憾的是，Collision Resistance这么重要的性质，在数学上的严谨证明是不存在的，因此我们只能凭借现实中的经验来判断一个哈希函数的抗碰撞系数高与低。

这一点在维基百科的 Collision resistance 词条中有一段阐述：
Cryptographic hash functions are usually designed to be collision resistant. However, many hash functions that were once thought to be collision resistant were later broken. MD5 and SHA-1 in particular both have published techniques more efficient than brute force for finding collisions. However, some hash functions have a proof that finding collisions is at least as difficult as some hard mathematical problem (such as integer factorization or discrete logarithm). Those functions are called provably secure.
这段话指出很多曾经被认为非常安全的哈希函数后来被找到了比暴力破解更加高效的破解方法，也由此被攻破（如MD5, SHA-1）

2.1.2 Hiding

即隐匿的，不可知的。啥意思呢，就是哈希函数的计算过程是单向的，完全不可逆的。这意味着我们可以通过一个输入x来求解一个H(x)，但通过H(x)却完全不能确定x的任何信息。

当然，我们上面提到了，由于暴力破解（Brute-force）这种方法的存在，因此完全不可逆的哈希函数是不存在的，顶到天上，我们可以把所有自变量枚举一遍，而后哪个自变量算出的哈希函数值与H(x)相同，则哪个值就是原函数值即可。

这就代表着，要写出一个尽可能 “Hidding” 的算法，首先需要输入空间（自变量取值）足够大，其次需要哈希函数值分布比较均匀。这才能尽可能加大攻击者破解这个算法的难度。

2.1.3 Digital Commitment

这个概念也被称为 Digital Equivalent of a sealed envelope

这玩意不是很好理解，东西可以看成一个电子密封信封，信封外的东西是完全公开的，而信封内的东西我们并不知道。但是我们又可以通过信封外公开的信息来确保信封内的东西没有被篡改过。

具体怎么达成的呢？
利用我们上方提到的 Hiding 特性，达成了通过公开内容（哈希值）无法得到私密内容（原输入）
利用上方的 Collision Resistance 特性，保证了只要私密内容被篡改了，则公开内容必然发生变化。

当然，上述两个目标是任何一个哈希算法都要兼顾的，但有些哈希算法的输入控件不够大，那就不满足 Hiding 这个基本要求。
此时我们常常采用附加随机数的方法，即在原输入后方加一个足够大的随机数，然后一并算出它们的哈希值。我们一般用 H(x||nonce) 来表示这个值。

• H:哈希函数
• x:原输入
• nonce:附加随机值

2.1.4 Puzzle Friendliness

注意，这个性质，是比特币（Bitcoin）中所额外要求的性质。

维基百科上这样描述这个性质：

Puzzle friendliness is a property of cryptographic hash functions. Not all cryptographic hash functions have this property.

Informally, a hash function is puzzle friendly if no solution exists, which is better than just making random guesses and the only way to find a solution is the brute force method. Although the property is very general, it is of particular importance to proof-of-work, such as in Bitcoin mining.

其意义为这个哈希算法目前为止不存在有效预测方法（只能 Brute-force）。它要求这个哈希值的计算是不能准确预测的，即我希望得到一个特定的哈希值，我只能通过枚举自变量来确定其正确输入。

看到这里，如果此前的内容都理解了，读者大概率会碰到这么个问题： Hidding 和 Puzzle Friendliness 这俩不是一个东西吗？

Difference between Hidding & Puzzle Frientliness

我们给出一个哈希值：y = H(x|r)，这里 y 是输出， x; r 是输入

对于Hiding而言，我们干的是这么一件事：

Given an output of a hash function (y), it is infeasible to find an input (x).

Note, r is not given.

而对于Puzzle Frientliness而言，我们干的是另一件事：

Given an output of a hash function (y) and part of the input (r), it is difficult to find an input (x).

Note, r is given.

所以 Hiding 希望你无法高效的找到完整的输入，而 Puzzle Frientliness 是已经给了你一部分输入，希望你无法高效的找到另一部分的输入。

好的，现在我们搞明白了两个性质的区别，那这又跟 Bitcoin 有啥关系呢？

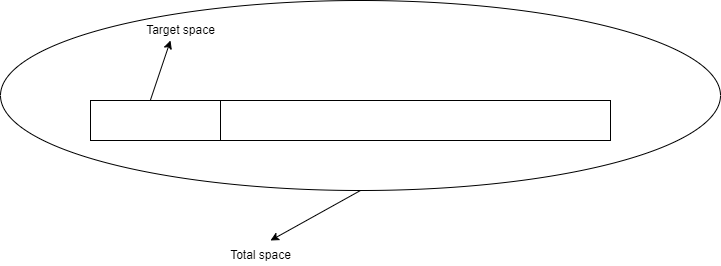
我们在这里简要的讲述一下 Bitcoin 的获取方法（即挖矿过程）

如上图所见，Total space 其实就是你能取到的所有哈希值（函数值域），而 Target space 是我们的目标，我们需要找到一个特定的输入，使得这个输入在进行哈希运算后取到的值恰好处于 Target space 内。

而在 Bitcoin 中，给出的输入格式是这样的：H(Block Header)，这其中，Block Header 内有很多的 域 ，这茫茫多的 域 中有一个名叫 nonce ，它就是我们能够设置的随机数。

挖矿的过程就是通过 Brute Force 的方法，持续不断的取随机数，算哈希，并找到了符合要求的哈希值的过程。而我们上面说的 Puzzle Friendliness 这个性质，就意味着这个过程没有捷径，只能暴力求解。

这种没有捷径的过程能够提供 工作量证明 ，即 Proof of work ，代表着你确实做出了足够的工作量来得到这样一个输入。

2.1.5 Difficult to Solve / Easy to Verify

通过上面的性质，我们很容易就能理解这个条目在讲什么。

我寻找一个有效的随机数 nonce 的过程是非常难的，需要大量的工作量。但我只要找到了这个 nonce ，别人要验证这个 nonce 是否正确是很容易的，因为验证过程仅仅需要一次哈希运算即可

额外提一嘴：

SHA-256 是 Bitcoin 中所采用的哈希算法。其全称为 Secure Hash Algorithm 。

2.2 签名（Digital Signature）

2.2.1 Symmetric Encryption Algorithm

即 对称的加密体系 ，也称 Symmetric-key algorithm 。

这个体系的目的很明确，在于加密，保证信息传输过程中不被窃取或篡改。

它采用的方法是：收发两端采用相同（或者经过简单的转化）的密钥来进行加密 / 解密操作。

Symmetric-key algorithms are algorithms for cryptography that use the same cryptographic keys for both the encryption of plaintext and the decryption of ciphertext. The keys may be identical, or there may be a simple transformation to go between the two keys.
—— Wikipedia

这种方法的前提在于有一个安全的渠道，能够将密钥安全的由 发送方 送给 接收方。这也是对称加密体系的弱点之一，密钥的分发非常不方便。

2.2.2 Asymmetric Encryption Algorithm

即 非对称的加密体系 ，也称 Asymmetric cryptography 。

非对称的加密体系采用了一对钥匙，即 公钥 和 私钥 。加密使用公钥，而解密使用私钥。在信息传输时，发送方 利用 接收方的公钥 来加密信息，并传给接收方，而后接收方再用自己的私钥来解密发送方传来的信息。

显然，公钥是公开的，而私钥必须要保管好，自己留着。

通过这个模式，解决了对称加密体系中密钥分发过于繁琐的问题。

2.2.3 与 Bitcoin 的关联？

在 Bitcoin 中，由于其采用 去中心化 的思想，因此是没有所谓的 银行 来管理你的账户的，一个(公钥；私钥)对就是一个账户。

我们形象的理解一下，公钥相当于你的账号，这是可以公开的，别人给你转账必须要得知你的公钥。而私钥相当于你的密码，只有知道你的密码的人才能够取出这个账户上的钱。

但是问题来了， Bitcoin 中好像并不需要这个对？因为它的哈希算法是完全公开的。

这就要引出这一主题的概念： 签名 。

2.2.4 签名

签名这一概念是为了保证一笔交易是真正由 署名的发起方 发起的，而不是有人冒名顶替的。

那这里如何保证这个发起方就是我呢？答案是我利用 私钥 来进行签名，而后所有人看到这笔交易之后都有权利利用我所公开的公钥来验证这个签名。

Two main properties are required:
First, the authenticity of a signature generated from a fixed message and fixed private key can be verified by using the corresponding public key.
Secondly, it should be computationally infeasible to generate a valid signature for a party without knowing that party’s private key. A digital signature is an authentication mechanism that enables the creator of the message to attach a code that acts as a signature.
—— Wikipedia

在 Bitcoin 中，一般是先对 message 进行哈希，而后对产生的哈希值进行签名。

Part3. 数据结构

3.1 哈希指针（Hash Pointers）

指针这玩意我们很熟悉了，在C和C++里面用的很多。

哈希指针概念与其类似，但额外加了点东西。它不仅要存储一个结构体的地址，同时要存储 这个结构体对应的哈希值 ，我们用 H() 来表示一个哈希指针。

A regular pointer gives you a way to retrieve the information. A hash pointer will let us ask to get the information back and verify that the information hasn’t changed. So a hash pointer tells us where something is and what it’s value was.

上面这段话很好的描述了哈希指针的好处，它不光可以获得信息存储的位置，同时也可以检测存储的信息是否遭到了修改。（具体方式可以回顾此前的 密码学原理 部分）

为什么我们要提到哈希指针呢？我们需要引出 区块链 这个重要内容。

3.2 哈希链表

字如其名，区块链本身是由一个个区块组成的链表。但这个链表有其特殊之处。其中一个最显著的特点，区块链中使用的指针是哈希指针。

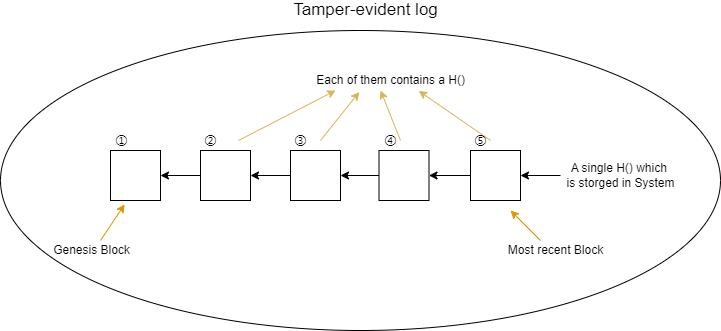
我们这里着重强调几个概念：

• Genesis Block: 即起始区块
• H(): 后续每个区块中都会有的哈希指针，这个哈希指针的哈希值是通过对它前面一整个区块的 所有内容（包括里面的哈希指针） 运算得到的。
• Most recent Block: 整个链条的最后一个区块，这个区块的哈希指针被保存在系统中。
• Tamper-evident log: 区块链能够实现的一个性质，我们能够看出，这一整个链条中无论哪个块的内容被篡改了，都会导致最终存储在系统内的哈希值发生更改。这代表着我们只要 记住最后的这个哈希值 ，就能够检测 一整个链表 是否被篡改过。

这种存储方式还有个好处：区块链是很长的，因此一个节点内不可能存储一整个链表的内容，这就表示如果我需要一个我没有保存的节点（我们称之为 节点1 ）的内容，则我需要向别的保存过 节点1 的节点（我们称之为 节点2 ）索取相应的信息。而哈希指针能够保证 节点2 给我的内容是正确的，而非经过篡改的。

我们需要额外提一嘴，哈希链表 不能是循环链表 ，因为如果带有环状结构，则会出现循环依赖，一个节点被篡改了，最终哪个节点的哈希值都定不下来。

3.3 Merkle Tree (Binary hash Tree)

我们应该比较熟悉 Binary Tree，就是普通的二叉树。

这里我们看到括弧里面的名字应该能想个大概，即哈希二叉树。

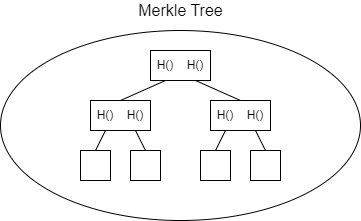
A hash tree, also known as a Merkle tree, is a tree in which each leaf node is labeled with the cryptographic hash of a data block, and each non-leaf node is labeled with the cryptographic hash of its child nodes’ labels.

我们还是说几个概念：

• Data block: 即 数据块 ，指整个 Merkle Tree 最底层的节点。
• Hash block: 即 指针块 ，指 Merkle Tree 上层的节点，每个节点内储存了其左右孩子的哈希指针。
• Root hash: 即 根哈希值 ，指对整个 Merkle Tree 最上面的节点取哈希，保存在系统中。

我们可以发现，与哈希链表很相似的是，只要整个 Merkle Tree 中哪一个节点被篡改了，最上面我们保存的哈希值就会发生改变。这也可以让我们很方便的得知整个数据是否遭到过篡改。

在Bitcoin中，每个区块之间利用哈希指针连接在一块，而每个区块内所包含的交易则通过一颗Merkle Tree进行组织。而每个区块内的 Block Header 内存放着这棵 Merkle Tree 的 Root Hash ；每个区块内的 Block Body 中存放着各项交易的交易记录。

3.4 Merkle Proof（Proof of Membership / Proof of Inclusion）

我们说回 Merkle Tree 。

Merkle Tree 的一大作用是提供 Merkle Proof 。这个玩意的意思是我需要证明 某一笔交易确确实实的发生了 。

在Bitcoin中，节点被分为 全节点 与 轻节点 ，全节点中包含了 Block Header 与 Block Body，这使得查询某一笔交易是否发生变得十分可行。

但轻节点中只保存了 Block Header（即只保留了哈希值），我们应该怎么证明这笔交易发生了呢？

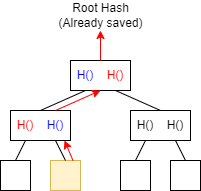
具体过程是这样：

• 首先，这个轻节点向某一个全节点发送请求，并附上它需要查询的交易位置（即图中的黄色块）。
• 此后，这个全节点计算出一条从这个底层交易节点一直连接到 Merkle Tree 的根节点的路径，这一条路径叫做 Merkle Proof（即图中红色箭头附加的路径） 。
• 全节点将路径上 未涉及到的全部哈希值（即图中红色的哈希值） 发送给轻节点。
• 轻节点接收到这些哈希值，从底层开始进行哈希运算【算出 指定交易的哈希（即第二层中的蓝色哈希值） -> 与第二层的红色哈希值 （在第三步中由全节点发给轻节点） 拼接起来，再次进行哈希运算，算出再上一层的蓝色哈希 -> 以此类推，直到 Merkle Proof 路径到头后，最后求一次哈希，与自己的 Block Header 中的内容相比较，判断出这笔交易是否发生过。

上面这个过程，就是从底向上进行验证的一个过程。

我们回头捋一下，这个从下向上的过程，时间复杂度是多少？
不难看出，是log(N)。

既然说了 Proof of membership ，那读者有没有想过，是否存在一种证明 Proof of non-membership （即证明某个交易并不存在）的方法？

有一种比较简单的证明方法是直接将整棵树发给轻节点，让轻节点验证一下这棵树没错，而后就完成了证明。但很显然，这种方法的时间复杂度是线性的。

我们需要申明，如果我们 对叶节点的排列不做任何假设 的话，是没有更高效的方法的。

但当我们能够对叶结点的排列做假设的时候，这个问题有一个很巧妙的解法。

我们假设叶节点是按照它们的哈希值进行有序排列的，现在要证明一笔交易（我们称之为交易1）并不存在。

• 我们先对 交易1 求一个哈希值，找到如果它在这棵 Merkle Tree 中时应当所在的位置。并根据这个位置找到其两侧的交易（我们称之为 交易0 和 交易2 ）。
• 而后轻节点向全节点发出请求，进行 交易0 与 交易2 的 Merkle Proof ，如果最终获得的结果是正确的，则说明 交易0 与 交易2 之间并没有插入一个 交易1 ，这就证明了 交易1 其实是不存在的。

上面这个过程通过两次 Merkle Proof 达成了 Proof of non-membership ，时间复杂度仍然是 log(N)。其代价是必须要对叶子节点（交易）进行基于哈希值的排序。

我们称这种针对哈希值排序的 Merkle Tree 为 Sorted Merkle Tree 。

在Bitcoin中，并没有采用 Sorted Merkle Tree ，因为 Bitcoin 中并没有 Proof of non-membership 的需要。

Part4. 共识协议

4.1 Double spending attack

我们先来考虑一下数字货币与实体货币的区别：

实体货币很简单，一手交钱，一手交货。因此交易双方只需要考虑这个货币究竟是不是真的，即现实中各种验钞机、货币上的各种防伪证明干的事情。

但数字货币不太一样。我们之前提到过非对称的密码体系（即公私钥体系），通过在货币上利用私钥签名，可以保证每个人都能通过公钥来对货币的真实性进行验证（如果读者对这个点不熟悉，请返回2.2.4）。但我们需要明确，数字货币是可以 被复制的 ，如果仅仅通过公私钥进行保护，那不能阻止某些人无限复制手中的这一份货币。因此这显然不能作为完整的货币体系。

我们称这种问题为 “双花攻击” ，即 double spending attack 。

这个问题在中心化的系统中也不算难解决，给每一份数字货币一个唯一的编号，并让唯一的一个中心机构维持一个数据库，里面记录一下当前这份货币在谁手里。双花问题看似很方便的被解决了。

但很遗憾，我们需要的数字货币是 分布式的 ，是 去中心化的 。

由此，我们转变一下思路，需要思考两个主要的问题：

• 在去中心化的货币系统中，谁有权力发行数字货币？
• 在去中心化的货币系统中，如何保证一个交易的有效性？

4.2 交易有效性保证

在Bitcoin中，存在两种哈希指针：

• 区块指针
• 交易源指针

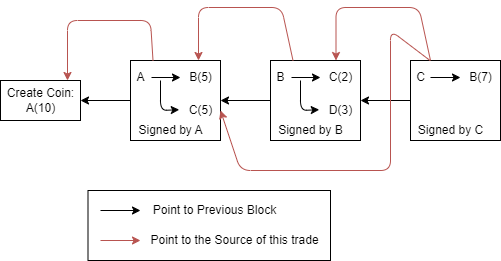
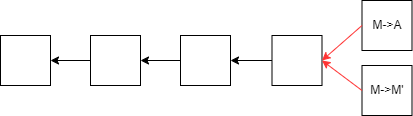
其中，区块指针与我们此前讲解的区块链大相径庭，它负责指向上一个区块。

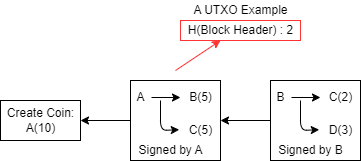
而交易源指针需要指向这笔交易的货币来源。比如：上图中A希望向B和C各转5个虚拟货币，则需要有一个指针指向A这10个虚拟货币的来源。

通过交易源指针，能够很好的防范双花问题，假设A再次尝试向外转账时，系统会进行交易回溯，从而查询到A手中的货币已经被花出去了，进而阻止这一次交易的发生。

好了，基本的原理我们搞明白了，我们现在需要详细的考虑一下一次交易的过程。

我们就以 A转给B 5个虚拟货币为例：

• A需要知道B的地址（也可以理解为账号），在Bitcoin中，这个账号是通过对B的公钥进行哈希，此后再进行一系列处理得到的。
• B要验证这笔交易是否合法，因此需要通过A的公钥验证A的签名，意味着B也需要知道A的公钥。
• 进一步思考，Bitcoin中全部用户都有权利验证一个交易的合法性（因为这是个去中心化的系统，这一步交易需要得到全部节点的认可），因此其实所有节点都需要知道A的公钥。

我们得知了上述三点要求后，需要引出区块链中每一笔交易的 输入与输出 。

其中，输入要求给出两点：

• 发起交易者虚拟货币的来源（即交易源指针）
• 发起交易者的公钥

输出要求给出一点：

• 收款人公钥的哈希

这里可能会有读者想到些安全问题，因为一个交易的公钥是由交易的发起人自己给出的，那如果B想要冒充A，但他通过自己的私钥进行 B的签名 并附上了 B的公钥 ，伪造了一个 由A向B的交易 呢，应该如何判别出这种窃取行为？

我们可以发现输入的要求中不仅要求一个公钥，还要求虚拟货币的来源。而这个来源也必定是一个区块，即 它也会有相应的输出 。

我们想想这个输出是什么？

这个输出必定是 A公钥的哈希 。

因此，防范上面的那种安全问题，只需要保证 这笔交易中提供的公钥 与 这笔交易中货币来源提供的输出（公钥哈希） 相匹配 即可。

（这地方有点绕，读者可以对着上面的图示比划比划）

4.3 区块

4.3.1 Block Header & Block Body

我们上面提到的案例，是一个非常简化的样例，因为我们假设每个区块内仅仅存在一个交易。显然，现实中一个区块内有很多交易，它们被存储在Merkle Tree中（关于这部分的内容，读者可以前往3.3进行回顾）。

我们还讲了，一个区块中一般包括区块头（Block Header）与区块主体（Block Body）。下面，我们详细给出其中的内容：

Block Header需要包括以下内容：

• Version: 使用的比特币协议版本
• Hash of previous Block Header: 指向前一个区块头的哈希指针
• Merkle Root Hash: 当前区块Merkle Tree根节点的哈希值
• Timestamp: 当前区块的时间戳，表示当前区块被挖出来的时间
• Target: 难度目标阈值
• Nonce: 随机数

Block Body需要包括以下内容：

• Transaction list: 交易列表

这其中，最后两个域是与挖矿相关的，读者可以回顾 2.1.4 部分的内容进行回顾，这里先不详述。

Version 的含义很简单明了。

Hash of pervious Block Header 需要强调一下，它指的是前一个 区块头 的哈希指针，并不包含区块主体。至于区块主体是否被篡改，则通过每个头中的 Merkle Root Hash 来进行保证。

4.3.2 Full node & Light node

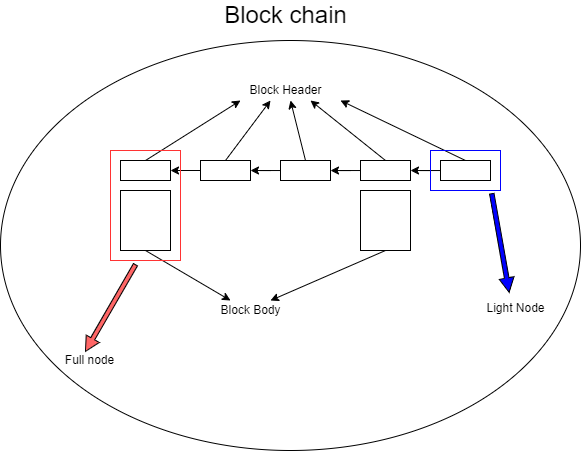
在此之上，我们进一步明确一个在 3.4 中提到过的概念，即 全节点(Full node) 与 轻节点(Light node) ，全节点又称为 Fully validating node ，轻节点又称为 Light weight node 。

全节点与轻节点的区别在于是否存储了 Block Body 中的内容。

因此，一般而言，轻节点是无法仅仅依靠自己来进行各种验证的，它需要向全节点进行查询请求，依靠全节点给出的各种信息来辅助验证。但由于轻节点比较节省空间，因此一个区块链内大部分的节点其实都是轻节点。

我们这里给出一个更合理，更详细的区块链图：

4.4 Distributed Consensus

该概念即 分布式共识 。由于区块链是个分布式账本，那这个账本应该如何决定一个区块 是否应该写入 ，以及 按照什么顺序写入，又应当如何保证 各个本地系统上能够保存相同的一个链条 ？这就是区块链内需要解决的分布式共识的问题。

A fundamental problem in distributed computing and multi-agent systems is to achieve overall system reliability in the presence of a number of faulty processes. This often requires coordinating processes to reach consensus, or agree on some data value that is needed during computation.
—— Wikipedia

这里得稍微提一嘴分布式共识的一些知识，有一个理论叫 CAP Theorem ，描述了分布式系统的三个希望能够达成的性质，但很可惜，三者之中至多只能选择两个。

这三个性质为：

• Consistency: 一致性 (Every read receives the most recent write or an error.)
• Availability: 可用性 (Every request receives a (non-error) response, without the guarantee that it contains the most recent write.)
• Partition tolerance: 分区可用性 (The system continues to operate despite an arbitrary number of messages being dropped (or delayed) by the network between nodes.)

In database theory, the CAP theorem, also named Brewer’s theorem after computer scientist Eric Brewer, states that any distributed data store can provide only two of the three guarantees.
—— Wikipedia

这个理论其实挺重要，但在区块链的文章中，我们不会过于详述。

4.5 Consensus in Bitcoin

在Bitcoin中，我们需要基于一个最基本的假设，即 有恶意的节点永远是少数 来实现分布式共识。

4.5.1 Sybil Attack

一种实现分布式共识的方法是基于所有节点的投票结果，即每个节点都进行对当前区块的合法性验证，如果判断它合法则投赞成票，如果赞成票过半，将当前区块写入链中。

这种方法是有很明确的破解方法的，我们此前提及过（2.2.3），在Bitcoin中，一个(公钥, 私钥)对就是一个账户，那恶意节点完全可以生成茫茫多的恶意账户，对于自己希望加入的非法区块（illegal block），让自己能够控制的所有恶意账户全部投赞成票。如果这些恶意账户数目足够多，则可以轻易破解这种投票机制。

我们称呼这种攻击方式为 Sybil Attack(女巫攻击) 。

Sybil attack is a type of attack on a computer network service in which an attacker subverts the service’s reputation system by creating a large number of pseudonymous identities and uses them to gain a disproportionately large influence.
—— Wikipedia

很显然，仅仅依据账户数目来进行简单投票的方案，是不行的。

4.5.2 算力优先

简单的投票方案不成立，并不能意味着我们就要放弃投票。

在Bitcoin中，采取的是一种很巧妙的限制方式。

我们此前提及，挖矿时需要通过取nonce值，计算nonce与Block Header其他部分拼接过后的哈希值来决定我们是否找到了正确的随机数。显然，这个计算过程需要大量的算力，而当我们找到了正确的随机数后，我们就得到了 记账权 ，即 向Bitcoin这个去中心化的账本中写入下一个区块的权力 。

显然，算力越强大，每秒钟能够尝试的nonce数目就越多（我们称这个数目为 Hash Rate），得到正确nonce的可能性自然越高，也就意味着我们有更大的权值来 “记账” 了。

这个机制在Bitcoin乃至Blockchain中都是极其重要的，因为它保证了，只要一个区块链的大部分Miner都是 诚实的 ，那么这一整个区块链的安全性就能得到相当程度上的保证。

当然，我们算出了正确的nonce，还是需要接受其他用户的验证的。因此我们需要将这个区块发布出来，让其他用户来检查我的nonce是正确的，并且我放进去的交易列表都是合法的。

4.5.3 Forking Attack

读者大概第一次读到这里还是一头雾水，上面这个原则看起来还是不十分严谨。比如：我如果挖出的区块不在主干上，额外挖到一个小分支呢？这账本不久分叉了吗？

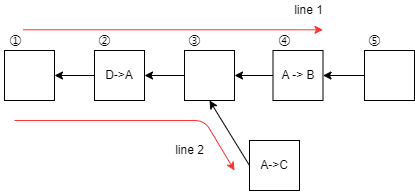
事实上，有这种攻击方式，即 Forking Attack(分支攻击) ，通过专门在Bitcoin这个帐本上附加分支来达到对交易的回滚目的。

我们可以看到，图中的链条出现了一条全新的分支，而显然，这条分支上 A->C的这笔交易与原链条④上A->B的交易是冲突的 ，但在写入区块时，如果不加限制，它们都会被判定为合法的，因为 两者都能通过回溯查询到有②中D->A的交易发生 。

这种情况显然是不应当发生的，它相当于对已经发生过的交易进行了一次 回滚 。因此Bitcoin中有相应的规定，称最长的那个链条为 Longest valid chain(最长合法链) ，并人为限制，每次新写入Bitcoin中的区块，都应当是在扩展最长合法链。

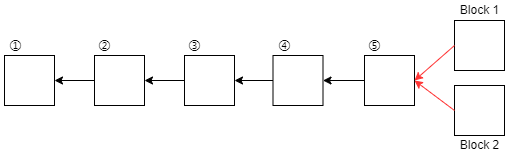
当然，还有一种合法的分叉可能性出现，即两个用户同时发现了正确的区块，并立即发布了出来，在这种情况下，其他用户都将暂时保留这两个区块，使得区块链变成下面这个样子：

这时，处理方法就是看谁快了，Block1 与 Block2 的哪个区块的下一个区块被先挖出来，系统就保留哪个。而另一个区块则被舍弃，被称为 Orphan Block 。

4.6 Block Reward

我们说完了记账权的争夺规则，但问题来了，这玩意又费电又费资源， （甚至搞得很多人为了这件事疯狂的去挖矿） ，图个啥，就图在那个账本里面记一笔嘛？

不知道读者还记不记得在Part4最开始提及的两个问题，我们现在只解决了第二个，即如何保证交易有效性。

现在要明确的，就是第一个问题，即 谁有权力发行货币 。

在Bitcoin中，发行新的比特币，只有唯一的方法，称为 Coinbase transaction ，除此之外的任何交易，都是将已有的比特币从一个账户上转到另一个账户上的过程。

相对应的，这个产生速度是在浮动的，在最开始的阶段，甚至达到了 50BTC per Block 。根据协议中的规定，每当21万个区块被发现过后，就需要将区块奖励减半。目前，这个产生速度已经降低至 3.125 BTC per block （May, 2024）。

在这里，还需要明确一点，对于Bitcoin而言，其产生新区块的速度为 10 minutes per block ，因此我们可以大概算出 Block Reward 减半一次所需的时间： 大约4年左右 。

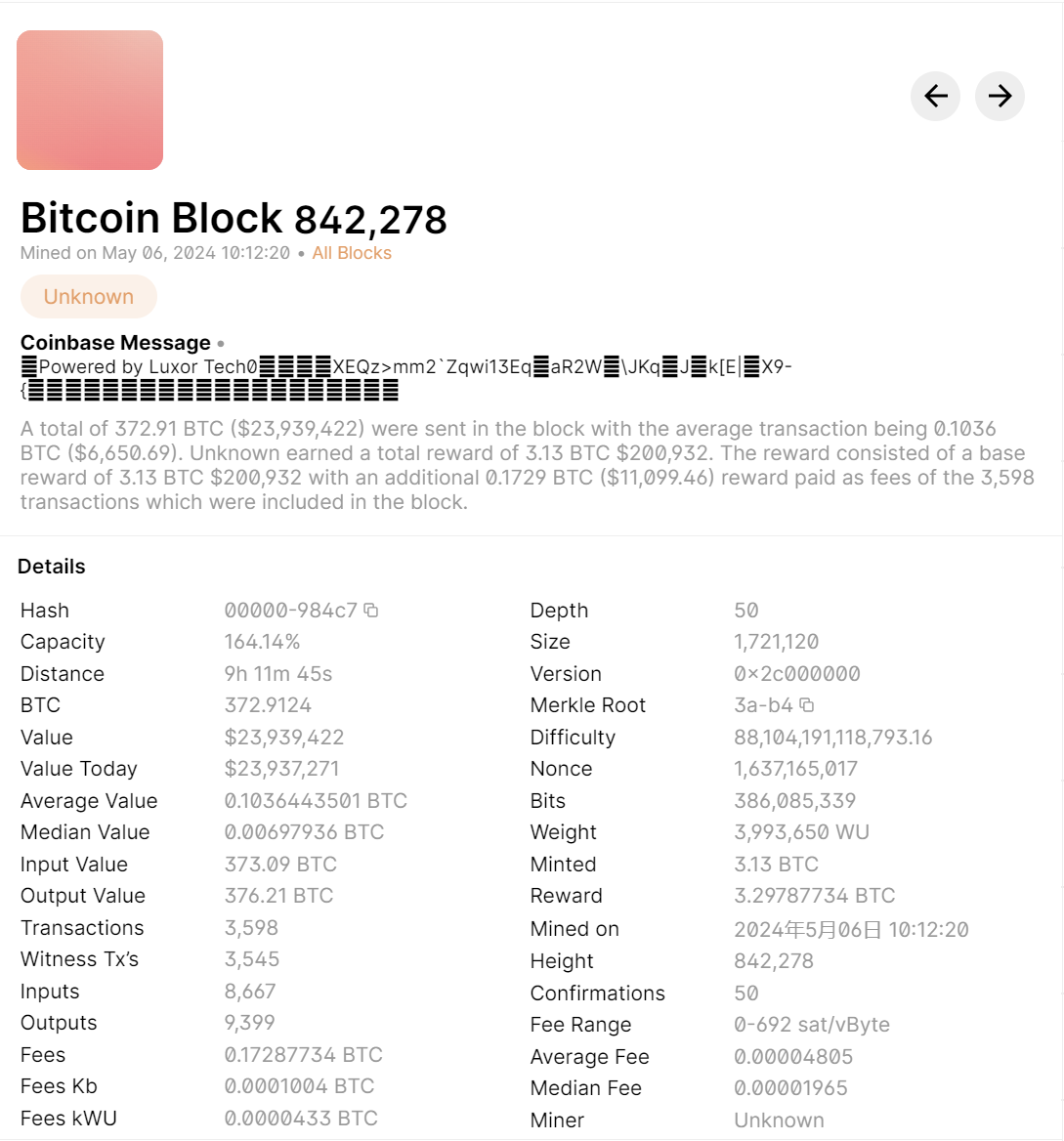
我们可以通过 blockchain.info 这个网站对于当前各类虚拟货币的情况进行查询，这里给出一个区块的例子：

同样，区块内所有的交易都会被公示：

有兴趣的读者可以自己前往上面提到的网站上看一看。

Part5. 实现

经过上面的描述，我们应该能够理解Bitcoin的大体原理，也能明白这是一个以交易为基础（ Transaction-based Ledger ）的虚拟货币类型。

这里还需要提一下，另一种虚拟货币，以太坊(Ethereum)采用的并非与比特币相同的 交易基础模型 ，而是以账号为基础的另一种类型，我们称之为 Account-based Ledger 。这种模型我们会在后文中提及。

5.1 UTXO

我们先介绍一个概念， UTXO ，即 Unspent Transaction Output 。

In cryptocurrencies, an unspent transaction output (UTXO) is a distinctive element in a subset of digital currency models. A UTXO represents a certain amount of cryptocurrency that has been authorized by a sender and is available to be spent by a recipient.
—— Wikipedia

简单的来讲，Bitcoin中具有很多的交易（包括 转账交易 以及 铸币交易），这一堆交易中，有些交易的交易额 已经被接收方再次花出去了 ，而另一些交易额 仍然可被接收方所支配 。我们称这些还未被花出去的交易额所构成的集合为 UTXO 。

UTXO中的每一个条目，都需要给出两部分内容：

• 产生当前交易的哈希值
• 这个输出是当前交易中的第几个输出

写到这可能有点产生歧义，我们给个图：

我们看到，在第二个区块中，A转给了B / C 各 5BTC ，而B在这之后将其花掉了，但C并未花掉。因此B在UTXO中就不存在一个条目来记录它（或者说，是原先记录的那个条目被删掉了），而对于C则存在一条UTXO（如图中红色框内所示）。

上述例子说明，每一次交易，都意味着删除一部分UTXO，同时又新产生一部分UTXO。同时，对于整个UTXO而言，总输入应当始终等于总输出，即 Total inputs = Total outputs 。

当然，在现实状况中，Total inputs >= Total outputs 的情况要更常见一些。这是由于区块链本身是个账本，而一笔笔交易（一条条账目）想要放入这个账本的话，是应当交一笔手续费的。而这笔手续费，就交给当前区块的记账权拥有者（把这个区块挖出来的人）。

这个机制被称作 Transaction fee 。

A Blockchain transaction fee is an amount that a user has to pay to the miners to have their transaction validated on the Blockchain.

到此，我们已经明确了Bitcoin中除转账外获得BTC的两种方式：即 Block Reward 以及 Transaction fee 。

读者可能会疑惑于后续的手续费应该如何收取？难不成再单开一个交易嘛？

事实上， Transaction fee 是与 Block Reward 一同通过区块中的铸币交易（Coinbase Transaction）一并转给记账权拥有者的。

在Bitcoin中，所有没有被确认的交易会放在一个单独的池子里面（暂且按照池子来理解吧），这个池子叫做 mempool ，而后一个矿工挖出了一个区块，系统会挑选合法的交易放入这个区块中（交易数额越大，优先级越高），而后再将这个区块发布出来，供所有人验证。

因此，当这个区块被发布出来后，意味着里面有什么交易已经定下来了，因此总共的 Transaction fee 也就被算出来了。

为什么要维护这个UTXO呢，这与我们此前在4.1 / 4.2中所说的 对于Double Spending Attack的防范工作有关。

每次交易之前，都需要查询这个UTXO，确保发起交易者的账户上有相应的金额，即UTXO中有相应的条目。否则这笔交易就不会通过。显然，有UTXO的存在，可以快速检测Double Spending。

由于Bitcoin是个分布式系统，因此UTXO的维护是每一个全节点的任务（应该还记得这个概念吧）。

5.2 难度升格

5.2.1 Block Header的数据结构

public:
    // header
    int32_t nVersion;
    uint256 hashPrevBlock;
    uint256 hashMerkleRoot;
    uint32_t nTime;
    uint32_t nBits;
    uint32_t nNonce;

上述代码块给出了Bitcoin中Block Header所包含的数据类型。

5.2.2 如何提升难度？

显然，在当前这个时代，算力膨胀，挖矿者的数目也膨胀，这代表着仅仅调整一个32位无符号的随机数nonce所带来的挖矿难度已经远远不够了。

Bitcoin需要尽可能控制挖矿难度使得每个新区块的发布时间在10分钟左右。因此，人们找到了另一个可以更改的内容，即上述结构中的 hashMerkleRoot 。

这玩意的数据类型叫 uint256 。

uint256 is an unsigned integer that can hold a maximum value of 2^256-1

那问题来了，这玩意不是MerkleTree的根节点哈希吗，怎么改？

我们应该还记得，Bitcoin中有一种交易是在区块被挖出来的时候由获得记账权的人自动得到的，即 铸币交易 （详见4.6）。这个交易内有一个单独的域被称为 Coinbase 域, 这个域内想些啥都无所谓, 而铸币交易也被包含在区块内的MerkleTree中, 因此可以通过进一步调整 Coinbase 域中的值来划定 hashMerkleRoot.

我们通常称呼这个 Coinbase 域内可调整的部分为 extra nonce, 在历史上, 它曾经取过 $ 2\space bytes / 4 \space bytes / 8 \space bytes $

因此，我们可以要求挖矿者在需要额外调整 extra nonce 的前提下来提高挖矿者的操作难度，进而一定程度上控制区块生成时间。

5.3 交易合法性验证

我们在 (4.2) 中提及，一笔交易合法需要提供交易发起者的公钥，以及此前的货币来源（一笔交易）的输出。前者就是一个公钥，后者则是一个公钥哈希。只需要保证二者配对，交易发起者再利用自己的私钥进行签名，即可保证这笔交易是合法的。

具体这个公钥和公钥哈希该如何配对呢？

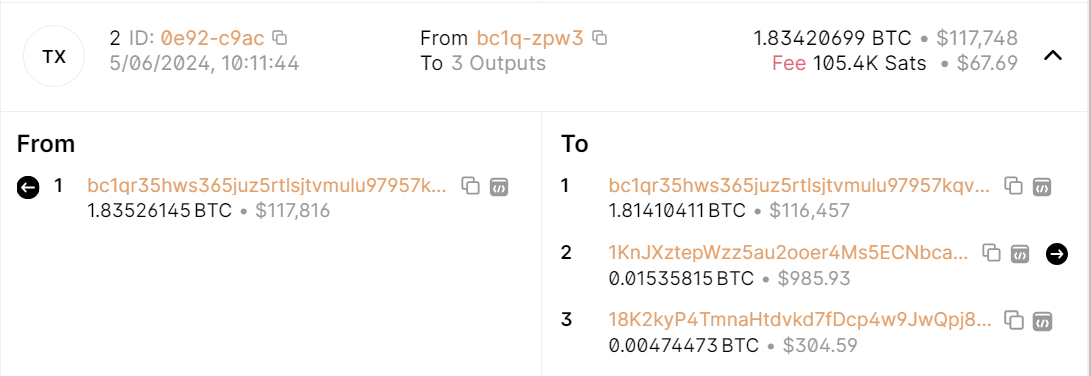
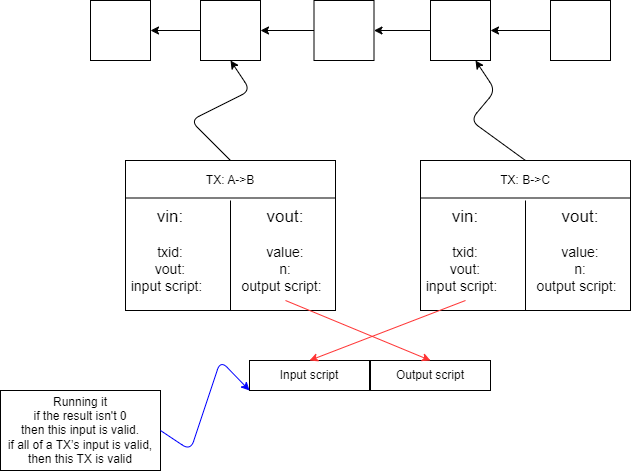
在Bitcoin的区块公示中，每一笔交易的输入与输出都会有一个脚本，在我们上文提到的网站 blockchain.info 中长这样：

当然，上面两个图片仅仅是举个例子，并不是配对的一组。

具体验证时，会将两个脚本（一个输入脚本，另一个输出脚本）拼在一起，尝试运行，如果能够成功跑通，则代表这笔交易的货币来源与交易发起者没问题。

5.4 简要的数学分析

我们对于挖矿的过程稍微分析一下。

每次取随机数，都可以看做一次 伯努利试验(Bernoulli trial) ，而挖矿的长期过程（一系列的尝试）可以看作一个 伯努利过程(Bernoulli process) 。

a Bernoulli trial (or binomial trial) is a random experiment with exactly two possible outcomes, “success” and “failure”, in which the probability of success is the same every time the experiment is conducted.

a Bernoulli process (named after Jacob Bernoulli) is a finite or infinite sequence of binary random variables, so it is a discrete-time stochastic process that takes only two values, canonically 0 and 1.
—— Wikipedia

而由于挖矿这个过程所需要尝试的次数实在过多，这个伯努利过程可以通过 泊松分布(Poisson process) 来进行近似估计。

与此同时，对于Bitcoin，系统设计的出块时间为10分钟，而出块所遵从的概率模型，为 指数分布(Exponential distribution) 。

至于为什么要按照指数分布来设计出块时间，是为了达成一个叫做 Progress Free 的性质。

5.4.1 Progress Free (Memoryless)

这个性质的意义是： 此前做过的工作并不能影响此后工作所需要花费时间的期望值 。

无情地说，此前如果未能挖出一个区块，那么此后挖出这个区块所需要花费的期望时间还是10分钟。

其实这个概念在概率论中叫做两次实验之间 相互独立 。说明上一次实验不会影响下一次实验成功的机率。

我们想想，如果没有这个性质，则算力高的人会理所应当的有不成比例的优势，因为他们失败的次数更多，会使得他们挖出新区块的概率相比于算力低的人们高十分多。事实上，这个性质恰恰是挖矿公平性的体现。

5.4.2 Geometric series

关于Bitcoin的总量，也可以通过数学的方法进行推导，这由Bitcoin中不断减半的铸币交易额度来决定。

具体来说，Bitcoin的发型会形成一个无限长的序列，前21万个数为50，随后21万个数为25，接下来12.5，6.25，3.125，…

上述数值持续相加：得到 210000 * 50 * (1+0.5+0.25+0.125+…)

最终有一个极限：两千一百万BTC(21 million)，这是Bitcoin设计的极限值。

当Block Reward最终减少到一定程度时，Bitcoin就相当于达到了其发行极限。

5.5 安全性说明

我们上面提到过 算力优先（4.5.2） 这个概念，并且在其中提到过这个机制极大程度上确保了区块链的安全性。

Bitcoin is secured by mining.

我们现在假使 诚实的节点拥有大部分算力 ，有恶意的节点仍然占有小部分算力。

可能会有读者产生疑惑，这意味着有恶意的节点仍然有几率挖出一个区块并获得其记账权，这也不安全啊？

因此，我们不妨考虑当有恶意的节点获得了区块记账权后，会发生些什么。

5.5.1 能偷走别人的货币吗？

假使，这个有恶意的节点希望从别人的账目上将货币转到自己账目上。

我们在 4.2 以及 5.3 中了解到了相应的保护机制，通过对应的机制，这个恶意节点永远无法 以合法交易的形式将别人账目上的货币转走 。

那假设恶意节点破罐子破摔了，我就是要把非法交易写进我这个账本中，会发生什么？

结果是，当他将非法交易写入时，由于这个过程是公开的，其它的诚实节点都能够检测到这个区块中的非法交易，因此，这个区块 不会被诚实节点所接受 ，又由于诚实节点占大多数，因此，这个含有非法交易的节点会如同 4.5.3 节中的 Orphan Block 一样被直接放弃掉。

显然，这样的攻击方式不仅无法让攻击者得到额外的货币，反而让他将原本能够拿到手的 Block Reward 也丢掉了。因此这种攻击手段并不成立。

5.5.2 Irrevocable Ledger

我们在这一部分中考虑一种很偷鸡的Double Spending。

之所以说它偷鸡，是因为我们这里所提及的 Double Spending 指的并非前面简单的双花，因为那种情况下，会很容易被系统检测出来，并判断为非法区块。

我们这里所指的 Double Spending ，是现实中通过比特币交易获利，而后通过分支攻击（Forking Attack）回滚那一笔比特币转账，最终达成不付出任何代价却现实中获利的效果。

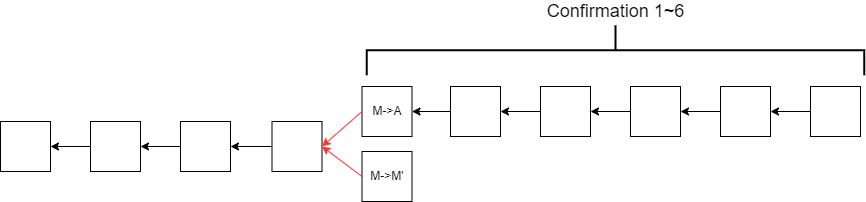
举例来说，M先在上方的区块内向A发起了交易，相应的，A在现实中也给予M相应的代价，而后M转头又挖出了底下那个区块，并使得底下那个区块变成了最长合法链（我们假设M有这个能力）。这使得M未支付相应的比特币就在现实中获取了相应的利益。

Bitcoin考虑到了这一点，并做出了相应的限制，即 只有交易发起的区块后方跟了5个区块后（即加上交易本身所在区块总共6个区块），才能算做交易成功 。这代表着即使M挖出了下侧的区块，由于上方的链条已经有一定的长度，因此进行上述的Forking Attack的难度大大增加（几乎不可能）。

我们管这种接在交易所在区块以及后方后面防范Forking Attack的区块统一取了个名字，叫该交易的 Confirmation 。显然，一笔交易的 Confirmation 需要等待长达1小时。但同样可以得到的是，这个确认的过程，能够使得交易的风险呈指数式的降低。

我们这里需要额外提一嘴，由于铸币交易(Coinbase Transaction)的特殊性(铸币交易产生了新的BTC)，它所需的Confirmation数目要远远高于正常的交易，它需要100个确认，即记账权拥有者需要等待接近1000分钟后才能真正将他通过一个区块铸币交易所获得的BTC花出。

当然，如果Bitcoin的交易非得让用户停在交易界面等一个小时，那未免太不便了一点。

一般而言，收款方收到交易通知与其发货之间是天然有时间间隔的。这意味着收款方只需要一直监听着区块的情况，等到最长合法链持续延伸，够长之后发货即可，这个过程可以完全由算法完成，不需要付款方或收款方一直等待。

5.5.3 控制交易写入

5.5.1 与 5.5.2 的目的是让这个有恶意的节点自己获利，现在我们都封死了。

那有没有一种可能，这个有恶意的节点故意不把某一部分合法交易写入来达成破坏呢？

答案是，应该不会，因为交易既然是合法的，则势必能被写入某个区块内（除非恶意节点能获得后方所有的区块的记账权，这几乎是不可能的），而恶意节点这么做的话，反而使得自己无法获得这笔交易的手续费（Transaction fee，详见5.1），降低了自己的收益。

5.5.4 Selfish Mining

有读者可能会有大胆的想法，我就摁想实现上面的那种 Double Spending ，我往前猛猛挖，挖出来6个块然后不发布，然后等到别人挖到相应的区块了，我一股脑把6个块的链条甩出来，直接使得最长合法链转移到我这里，不就实现了Forking Attack了吗。

显然，这种攻击的可能性在理论上存在，但需要考虑，挖出区块的可能是与算力成正相关的，因此，恶意节点算力占比如果比诚实节点低，则这种攻击的成功可能性仍然很低，因为理论上来讲，恶意节点挖的不可能比诚实节点快。

如果恶意节点占了大多数算力，这种攻击的成功概率才比较高。 （一种货币让恶意节点在投票基础中占据了大多数的权重，那这种货币离报废也不远了…）

Part6. 网络

这一部分的内容涉及到一些计算机网络原理的内容，不会太深

6.1 Basic description

Bitcoin的协议运行在应用层（ Application Layer ），也是整个计算机网络七大层中的最上层。

而由于Bitcoin基于分布式系统进行工作，因此在最底层的应用层原理上, 运行着一个 P2P 协议.

至于更下层的传输层和网络层, 则是常规的 TCP / IP 协议

关于 Peer to Peer overlay network

A peer-to-peer overlay network is a computer network built on top of an existing network, usually the Internet. Peer-to-peer overlay networks enable participating peers to find the other peers not by the IP addresses but by the specific logical identifiers known to all peers. Usually, peer-to-peer overlays have the advantage over the traditional client-server systems because of their scalability and lack of single-point-of-failure. Peer-to-peer overlays are commonly used for file sharing and realtime data streaming.

P2P 协议与传统的 客户端-服务器协议并不一致，在该协议中，所有的终端的地位是对等的，而他们也不需要通过传统的IP来寻找对方，而是可以更便捷的通过特别的逻辑标识符在互相之间建立连接通道。

需要特殊说明的一点是， 有些P2P网络 并非 完全的去中心化 ，在它们的网络中，还存在着 Super Node(Master Node) 这种核心节点。

在Bitcoin中，是完全去中心化的，即每个节点的地位 完全对等 。用户想要加入这个网络，只需向一个种子节点( Seed Node )发送连接请求，而后种子节点就会将它已知的所有节点告知这个新人节点，周而复始。

这一过程中，通常在介于 Application Layer 与 Network Layer 之间的 传输层( Transport Layer )上，使用的是TCP协议，这一方面是保证连接稳定性，另一方面目的也在于更好的穿透防火墙（如果读者对于计网的知识有一定的了解，应该听说过很多防火墙是拦截UDP流量的）。

至于退出整个区块链网络，则不需要用户做些什么事情，当别的节点长时间未能从你这里获得报文时，会自动将你从网络中删除。

6.2 Simple, Robust but not Efficient

如标题所言，Bitcoin的网络的设计原则是： 简单，鲁棒但并不高效 。

我们这样说的原因如下：

1. TCP, not UDP: 显然，TCP中要求的三次握手过程相比于UDP的尽力而为，在时延上要慢很多。

2. Flooding Network: Bitcoin中的信息传输采取泛洪策略，即每个节点向他周边的节点发送它新收到的消息。

   具体而言，一个节点收到了一个合法的交易，它会向所有与它相邻的节点发送这条交易，以便于让所有节点将这笔交易放入当前区块中。同时，每个收到这条交易的节点都会对这笔交易进行相应的标记，这是用于防止交易重复记录的。

   当然，还需要说明的是， 与它相邻的节点 并不意味着地理意义上的相邻，Bitcoin中的相邻是不考虑底层的拓扑结构的，这意味着很可能两个相邻的节点所处的位置相隔大洋两岸。

Gossip Protocol

这玩意是比特币使用的泛洪协议，简单描述如下：

A gossip protocol or epidemic protocol is a procedure or process of computer peer-to-peer communication that is based on the way epidemics spread. Some distributed systems use peer-to-peer gossip to ensure that data is disseminated to all members of a group.

上述两个原因也决定了，Bitcoin中区块的大小是有严格限制的，这个限制值是 1M 。

看起来很小对吧，但是由于以上的网络设计，即使是 1M 大小的区块，要传遍大多数节点，也需要10s以上的时间。

Part7. 挖矿难度

7.1 系统定义

我们在这一部分再对挖矿的难度进行一定的说明。

我们还是搬出这张图，明确以下条件，成功发现区块的条件是H(block header)<=target，并且再强调一下，Bitcoin使用的是SHA-256的哈希算法，这意味着它的哈希输出空间只有 2^256 这么大。

显然，有一种关系很好理解，即挖矿难度与目标阈值的取值是成反比的。

用一种更加严谨的定义来说：

$$ difficulty = \frac{difficulty \ 1 \ target}{target} $$

上式中我们解释几个量：

• difficulty: 挖矿难度，最低为1
• target: 目标阈值
• difficulty 1 target: 难度为1时的目标阈值(即目标阈值的最大值)

因此我们明确了调整难度的方法，对target目标阈值进行调整即可。

我们在5.2中提及过难度升格的问题，由于算力膨胀，设备先进程度的上涨，如果不对挖矿难度进行调整，则必定会使出块时间不断变短。

7.2 为什么要划定出块时间？

我们不妨思考一下，出块时间太短会发生什么。

我们前方提到过一个概念，叫做分支(Forking)。而有一种分支是合法的，即在很相近的时间内，两个节点同时挖出了当前区块的后续区块(详见4.5.3)。

如果出块时间太短，显然出现这种合法分支的可能性会大大增加。而每一个分支都必定会有一定的算力分配到上面进行进一步的挖掘工作（这取决于节点先收到哪个分支的声明，详见6.2），这意味着诚实节点的算力被更大程度上的分散了。

算力分散会发生什么事情？

我们考虑Forking Attack，原先二分支的情况下，恶意节点想要回滚交易，如果需要保证成功率，需要占据51%的算力总额（这样它才有把握挖的比诚实节点快，抢走最长合法链条），但出块时间过快，导致诚实节点算力分散了，分配到每个分支上的算力只占总算力的10% ~ 15%，那么，恶意节点只需要20% ~ 30%的总额算力，就能极大程度上保证分支攻击的成功率。

这很大程度上降低了安全性。

7.3 怎么调整目标阈值

首先，我们得明确目标阈值的调整间隔。

具体而言，对于Bitcoin，规定为每隔2016个区块，要调整一次目标阈值（换算下来大概两个星期调一次）

具体怎么调整呢：遵循这个公式：

$$ target = target * \frac{Actual \ Time}{Expected \ Time} $$

这个公式我们解释一下：

• ActualTime: 指的是系统最近产出2016个区块花费的时间
• ExpectedTime: 指的是系统期望的产出2016个区块应当花费的时间，即 2016*10 min(almost 2 weeks)

通过这样的设置，我们实现了令target阈值与当前算力的微妙同步。

在实际代码中，为了避免一些意外情况，ActualTime比8个星期还大，抑或是比半个星期还小，系统中也只会将其控制在 [1/2weeks, 8weeks] 这个区间内。即target的变动阈值在 [1/4target, 4target]之间。

请注意甄别： 挖矿难度 & 阈值

对于Bitcoin而言，挖矿难度与阈值负相关的，即阈值越小，挖矿难度越高。（读者可以对照着2.1.4的图理解一下这句话）

我们给出另一个公式，也是正确的，不过这次我们的主元是挖矿难度 difficulty ：

$$ next \ difficulty = previous \ difficulty * \frac{Expected \ Time}{Actual \ Time} $$

可以发现，后面的分数反过来了，这正是挖矿难度与阈值负相关的证明。

至于为啥要再写个概念呢，因为实际代码里用的是目标阈值target，但这个东西有点反直觉，因此又设置了一个挖矿难度，方便理解，量化。

Part8. 关于挖矿本身

8.1 挖矿设备

随着事件发展, 挖矿的设备逐渐趋于专业化, 这是因为传统的PC与挖矿的需求并不相同.

传统PC的部件中有一大部分的部件都用做与挖矿无关的方向, 如 显示方面, 意外处理方面等 , 但挖矿显然并不需求这些方面的专业性, 挖矿的唯一标准, 在于 算力 .

最初的挖矿是利用 CPU 进行挖矿, 但很显然, 挖矿这个对于随机值的计算过程, 使得CPU只有数值运算的相关部件(详见 计算机组成原理 章节 )在全程运转, 而其余很多部件都处于闲置状态, 效率不高.

而后, 挖矿这个过程使用的设备, 就走向了GPU的方向. GPU相比于CPU, 尤其擅长 通用并行计算 , 这就代表着它确实更加长于挖矿.

但仍然需要明确, 即使利用 GPU , 仍然是一种相当程度上的资源浪费, 这是因为GPU里面很多的部件仍然处于闲置状态, 一个典型案例即 GPU中的浮点计算模块 , 这个模块在机器学习等过程中是相当重要的, 但对于BTC挖矿(只涉及到整数运算的各种操作), 则几乎无用.

为了进一步提升资源利用率, 有一类专门的芯片被设计出来, 它被称为 ASIC(Application-specific integrated circuit) :

An application-specific integrated circuit (ASIC /ˈeɪsɪk/) is an integrated circuit (IC) chip customized for a particular use, rather than intended for general-purpose use, such as a chip designed to run in a digital voice recorder or a high-efficiency video codec.

这一类芯片是专门针对某一类型的应用特化的芯片, 它没有多余的运算部件, 仅仅针对于应用需求最重的领域进行特化, 可以达到相当高的利用率, 性价比是最高的.

当然, 不同的加密货币可能注重的计算方面也不同, 这代表着针对某一种加密货币设计的ASIC芯片, 也只能挖这一特定的加密货币(说明其通用性不高). 因此, 如果读者对于前些年的矿潮有所了解, GPU仍然是最火热的挖矿设备.

当然, 使用ASIC芯片挖矿的群体仍不在少数, 这就代表着通用性也是某些新型加密货币所需要考虑的内容. 因此, 有些新的加密货币会使用与此前火热的加密货币(如BTC) 相同的 Mining Puzzle , 这使得本来设计出用于挖传统加密货币的ASIC也可以用于挖这种全新的货币. 这通常用于 新型加密货币打开市场, 提升人气的时期 使用.

8.2 挖矿规模

挖矿的另一种趋势, 是 矿池 的出现.

这种现象的本质原因在于, 如果所有矿工均以个体作战, 则对于每一个个体, 这种收益是非常不稳定的. (三年不开张, 开张吃三年)

而为了保证收益的稳定, 出现了一种团体, 它将很多矿机集体集合起来统一调配.

在明确矿池的出现的根本原因前, 我们需要回顾一下 全节点 与 轻节点 的概念:

• 全节点
  • 一直在线
  • 在本地硬盘上维护完整的区块链信息
  • 在内存中维护UTXO集合, 便于快速检验交易的正确性
  • 监听BTC网络中的交易信息, 验证每个交易的合法性
  • 决定哪些交易会被打包到区块中
  • 监听别的矿工挖出来的区块, 验证其合法性
  • 挖矿
    • 决定沿着哪条链挖下去?
    • 出现等长分叉时, 选择哪一个分叉?
• 轻节点
  • 偶尔在线
  • 只保存每个区块的块头(Block Header)
  • 只保存与自己相关的交易
  • 只能检验与自己相关的那些交易的合法性
  • 可以验证挖矿的难度
  • 可以检测哪个是最长链, 但没有判断最长合法链的能力

显然, 如果想要挖矿, 则必须保证全节点的稳定性.

我们前面在挖矿设备中提到了, ASIC芯片只能从事挖矿本身需要的计算功能, 只有ASIC是无法维护全节点的其余功能的.

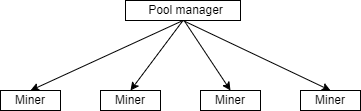
因此, 我们上面的挖矿团体, 即 矿池 就出现了:

• Pool manager
  • 也称矿主
  • 负责除了计算之余的全节点内容
  • 负责组装区块, 将需要计算的哈希值任务通过特定的通讯协议分配给矿工
• Miner
  • 也称矿工
  • 负责哈希值相关的计算
  • 当运算出对应的结果后, 通过特定的通讯协议将结果回馈给矿主
  • 当出块后, 参与分红

这带来的一种隐性好处在于, 每个个体只需要购买相应的设备, 加入矿池, 然后让矿主控制所有矿机的调度即可, 很简单. 此外, 如果一个人的收益过于不稳定, 那就一群人一块挖, 挖到了大家分红, 由于总算力的大幅提升, 这就使得收益稳定了不少.

那么, 问题又来了, 如何分红?

读者应该能想到, 这里又涉及到了我们此前提到的 工作量证明 这个概念. 矿池中的所有矿工需要向矿主提交自己的工作量证明, 以达到在最终分红环节中拿到更多的份额.

这个工作量证明如何提交呢?

我们回到最初矿池的建立根源上, 即找到区块当前要求的 nonce 的难度太高了, 这个限制区域太小了, 很难找到.

因此有一种很简单的工作量证明, 即矿主 人工划定一个较低的难度区间, 它比原区块要求的nonce的要求要低不少(我们称之为 share ) , 符合这个 share 要求的区块被称作 Almost valid Block , 同时矿主维护一个 每个矿工挖到 Almost valid Block 数目的列表 , 当一个矿工挖到了一个符合 share 的随机数后, 它向矿主提交这个值, 矿主将其对应列表中的值+1. 最终出块奖励按照这个列表中的值进行分配.

需要明确, 这种Almost valid Block除了作为工作量证明之外, 是完全无用的. 换言之, 它只能作为一种分红凭证在矿池的机构中起作用.

此外, 为了保证矿工 挖出区块后会如期交给矿主, 而不会自行发布 , 矿主会在组装的区块中的铸币交易的收款人地址中填入自己的地址.(铸币交易以及相应的更改见 5.2.2)

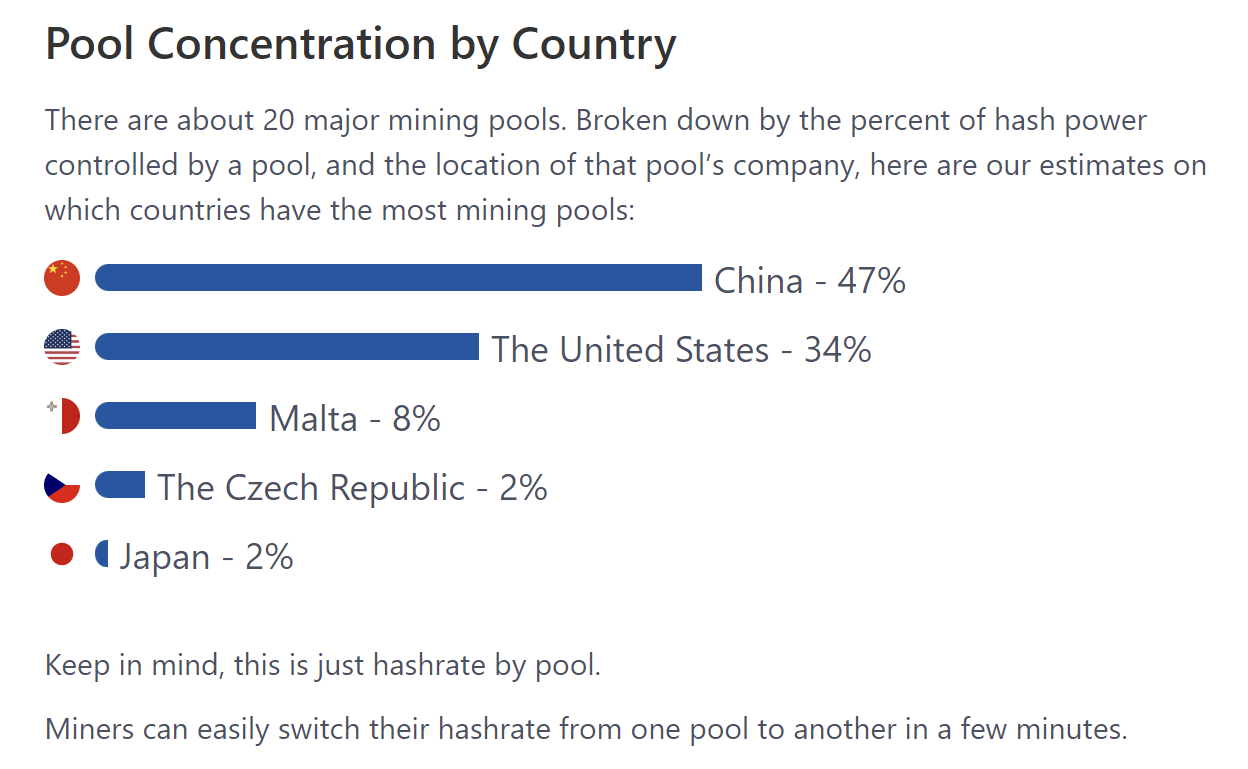
这里也给出当前矿池的国家分布:

—— From https://www.buybitcoinworldwide.com/mining/pools/

矿池的出现固然有其好处, 但它本质上其实是一种对 去中心化 的破坏, 想象一下, 有一个矿池吸引了足够多的矿工, 使得这个矿池的算力总和达到了51%以上, 那么他其实可以很容易的发起各种各样的攻击, 因为他占据了大部分的算力. (更恐怖的是, 其下属的矿工甚至不会意识到这一点, 这是因为下属矿工 只会接收到具体任务, 而并不知道这个任务是在以什么为目的 . 举例而言, 矿主可以很轻易的将下属的所有算力都转向另一条链, 达成分支攻击)

同时, 矿池的矿主是需要收取一定的管理费的, 他们经营矿池也需要盈利手段. 而矿池的火热程度, 很大程度上取决于矿主收取管理费的多少.

Part9. BTC的脚本语言

谈及脚本, 可能大部分读者会想到C, C++等编程语言, 与之不同, 比特币的脚本语言相当简单, 其唯一能够访问的对象就是一个堆栈, 这也意味着它不存在所谓 “全局变量” , “局部变量” 等概念. 也由于BTC的脚本主要基于堆栈, 因此也称之为 Stack based Language .

9.1 BTC的交易结构

result{
  txid: \\Transaction id
  hash: \\Transaction hash
  version:
  size:
  locktime: \\Could be included in a block after ...
  vin: \\Input
  vout: \\Output
  blockhash: \\The hash of its Block's Head
  confirmations:
  time: \\the time when this transaction appears
  blocktime:  \\the time when its block appears
}

vin{
  txid:
  vout: \\this transcation spent which output of last transaction
  \\(one transaction may conclude many output)
  scriptSig{ //or input_script
    asm:
    hex:
  }
}

vout{
  value: //the amount of BTC this output spent
  n: //output number
  scriptPubKey{ //or output_script
    asm:
    hex:
    reqSigs: //number of Signature which is required in this output
    type:
    addresses:
  }
}

9.2 BTC交易脚本的执行方式

9.2.1 交易脚本执行顺序

这幅图的原理其实在 4.2 节中有所提及, 读者如有遗忘可以再次前去复习一下;

实际执行中, 通常将输入脚本放在输出脚本的前方, 分别执行(为了安全性考虑).

9.2.2 几种具体的交易脚本

BTC中, 有以下几种十分常用的交易脚本:

• P2PK: Pay to Public Key
• P2PKH: Pay to Public Hash (Most Common)
• P2SH: Pay to Script Hash

我们一个个来看

1.P2PK

这种最简单的脚本中:

• input script:
  • Signature
• output script:
  • Public Key
  • CheckSig

请注意, 这里的output script 是 这笔交易使用的货币来源的输出, 并不是这笔交易本身的输出 !

按照堆栈的方法, 该类型脚本会将签名先压入栈底, 随后将交易来源的输出(即对应的公钥)压入栈顶, 最后利用CheckSig压入栈顶进行验证, 返回值只会是 True 或 False, 对应合法或不合法.

2.P2PKH

这种脚本中:

• input script:
  • Signature
  • Public Key
• output script:
  • DUP(Duplicated)
  • Hash160
  • Public Key Hash
  • EqualVerify
  • CheckSig

与P2PK不同, 这种脚本的输入既需要给出签名, 还需要给出本人的公钥, 而输出脚本给出的是 收款人公钥的哈希

从上往下看:

由于这种方式其实是最常用的, 因此这里会详细解释一下整个验证过程. 我们用Bottom表示栈底, Top表示栈顶

首先, 签名入栈, 公钥紧随其后入栈, DUP代表将栈顶元素复写一份, 即当前:

$$ Bottom \leftarrow Sig \leftarrow Pub Key \leftarrow Pub Key \leftarrow Top $$

Hash160表示将栈顶元素取哈希:

$$ Bottom \leftarrow Sig \leftarrow Pub Key \leftarrow Pub Key Hash(from \space input) \leftarrow Top $$

下面将输出脚本中的公钥哈希压入栈:

$$ Bottom \leftarrow Sig \leftarrow Pub Key \leftarrow Pub Key Hash(from \space input) \leftarrow Pub Key Hash(from \space output) \leftarrow Top $$

这里需要再次明确, 此处 靠近栈顶的公钥哈希, 是来自输出脚本的 (即别人把这个钱转给你的时候写的公钥哈希); 而 它下面的公钥哈希, 是来自输入脚本的 (即你要花这个钱了, 你自己给出的公钥通过哈希算法求出来的)

随后EqualVerify, 代表弹出栈顶两个元素, 比较两者是否相等.

最后一条CheckSig, 给出最终返回结果.

读者如果有兴趣, 可以返回 5.3 节看看我们在那里给出的脚本, 使用的就是P2PKH.

3.P2SH

这种方式是最复杂的一种方式, 其结构如下:

• input script
  • …
  • Signature
  • …
  • serialized Redeem script
• output script
  • HASH 160
  • Redeem script Hash
  • EQUAL

本处, 输出脚本中给出的不再是公钥或公钥哈希, 而是一种特殊的脚本的哈希, 该脚本名为 赎回脚本 , 而输入脚本中给出的是 赎回脚本的具体内容 , 以及 能使这个赎回脚本正确运行所需要的签名 .

当验证时首先验证输入脚本中的赎回脚本是否能与输出脚本中的哈希匹配(即 Serialized Redeem script 与 Redeem script Hash 的匹配), 随后还需要验证赎回脚本是否能够正确运行. 只有两步验证都通过, 该交易才能够视作合法.

至于这个赎回脚本的方式, 可能是前面提到的P2PK, P2PKH其中之一.

这种方式有点类似于编程语言中的函数封装, 将前两种验证方法封装成了一个单独的赎回脚本.

9.3 MultiSig(多重签名)

三种方式讲完了, 现在我们来说说这第三种到底干嘛使的, 因为P2SH这东西实在是有点复杂, 看起来很不必要.

第三种P2SH的最主要应用在于 实现多重签名(MultiSig) .

9.3.1 多重签名的概念与最初实现

所谓多重签名, 即一个账户中的钱由多个主体共同管理, 比如3个人管理同一个账户中的钱, 只需要两个人的签名, 就能够将钱取出. 最早的BTC所支持的多重签名如下:

• input script
  • False
  • Sig_1
  • Sig_2
  • …
  • Sig_M
• output script
  • M
  • PubKey_1
  • PubKey_2
  • …
  • PubKey_N
  • N
  • CheckMultiSig

其中 M 代表所需要的签名数, N 代表总共有几个签名. 至于Input script中的False, 那是Bitcoin最初设计MultiSig时的代码错误, 但由于其完全分布式的特性, 导致通过系统更新的方式修正它又显得代价过大, 因此采取的一种补偿措施.

这种方式在运行上没有任何问题, 但很明显, output script实在是过于冗余了, 同时我们考虑一下, output script通常是别人给你转账的时候需要使用的, 因此这就显得十分不方便.

9.3.2 利用P2SH实现多重签名

如何利用P2SH实现多重签名? 即将上述内容中的输出脚本单独封装:

• redeem script
  • M
  • PubKey_1
  • PubKey_2
  • …
  • PubKey_N
  • N
  • CheckMultiSig
• input script
  • False
  • Sig_1
  • Sig_2
  • …
  • Sig_M
• output script
  • Hash160
  • Redeem script Hash
  • Equal

此时, 输出脚本变得十分的简单, 这个Redeem script可以直接通过收款方主动公布得知, 因此大大提升了用户生成转账交易的便利性. 同时, 也对收款方的转账策略有了更高的保密性.

9.4 Proof of Burn(BTC销毁证明)

这是一种非常特殊的BTC输出脚本, 该脚本中有一行语句:

• output script
  • RETURN
  • …(nothing or more operations or text)

在BTC的机制中, 当脚本运行识别到 RETURN 这个语句时, 会无条件返回False, 而其后方的操作, 或任何文字都不会被执行. 这就意味着, 如果有一笔交易的输出脚本包含了 RETURN, 那么这笔钱就永远花不出去了, 也就代表着这一部分 BTC 被 销毁 了.

为啥要销毁比特币呢?

第一种可能是以一定的代价来换取某一些小币种(AltCoin, or Alternative Coin), 这些小币种通常需要你付出一定的代价来获取一定量的它们的货币.

第二种可能, 这种方式可以用来永久存储一些信息, 这是因为RETURN后方的一切内容都不会执行, 但也不会被删除(区块链的不可篡改性). 典型的例子比如Digital Commitment(详见2.1.3节) , 你可以将你所拥有的任何信息的哈希值写入这笔交易输出脚本RETURN的后方, 当需要证明你的所有权时, 只需要公布该交易内容以及相应的原件即可.

这种证明代表着, 任何一个用户, 哪怕是一个普通的使用者, 都可以以及其小额的代价, 换取在区块链中记上一笔, 写一些东西的机会.

Part10. BTC中的分叉

在此前的章节中曾经提及过多次 分叉(Forking) 这个概念, 在本章中我们进一步明确分叉的各种类型与作用.

分叉, 一般分为:

• State Fork: 对于区块记账权的争夺, 或由于本身区块链状态导致的分叉
  • Normal Fork: 两个节点几乎同时挖到了符合要求的区块, 这种分叉是合理的
  • Forking Attack(Deliberate Fork): 即有意产生的意见分歧导致的分叉(见4.5.3)
• Protocol Fork: 由于协议本身需要更新导致了分歧, 导致的分叉
  • Hard Fork: 即 硬分叉
  • Soft Fork: 即 软分叉

由于此前我们对于第一种 State Fork 的内容已经有了比较详细的解释, 因此我们这里主要针对 Protocol Fork 进行阐述. Protocol Fork 针对着对区块链本身的协议进行更新.

10.1 Hard Fork

所谓 硬分叉(Hard Fork) 即当比特币的协议需要进行根本性改变(即不认可这个更新的节点, 我们称之为 旧节点 对于新协议是不兼容的), 但有一部分节点对这种新的更新不认同时, 就会产生所谓的硬分叉.

一个非常典型的案例即 增加BTC中划定的区块大小上限 . 显然, 不认可大区块的旧节点无法认可新产生的链条.

为啥要增加区块大小 ?

比特币的区块大小最初被规定为 1MB , 即 $ 1 * 10^{6} \space byte $ , 这是什么概念? 传统一笔交易的平均大小约 $ 250 \space byte $ .

这代表着一个区块内可以包含的交易数目:

$$ \frac{10^6}{250} \approx 4000 $$

我们将其平摊到 10分钟 之内, 可以算出每秒钟的平均交易数目:

$$ \frac{4000}{10 * 60} \approx 7 \space tx/sec $$

显然, 这个每秒交易量太少了, 也代表着比特币的交易效率其实相当的低下.

因此, 有人提出需要增加BTC的区块大小.

我们现在想一想增加区块大小的具体情况:

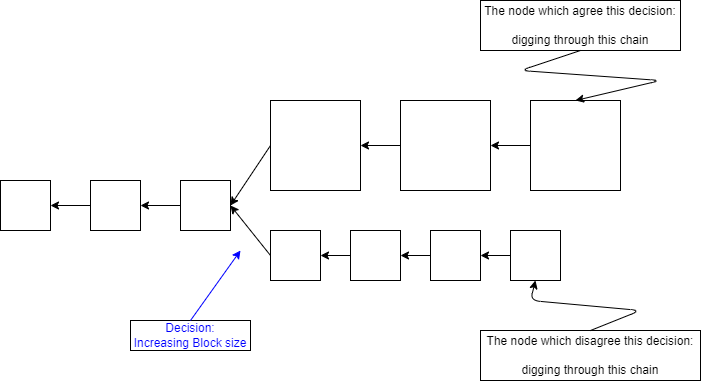
即使有大部分节点同意这个决定, 即增大区块大小, 但少数保守派不配合, 始终不认可这个决策, 那么这部分节点永远不会沿着上面的链条挖掘(因为在他们看来, 上面的链条是非法的), 而是继续沿着下侧链条继续工作. 这就形成了一个 硬分叉 .

需要明确, 这种分叉是无法消除的, 因为意见分歧一般无法统一(分布式系统就是会产生这种情况), 那么上下两侧的区块奖励怎么算?

一般而言, 出现硬分叉后, 会出现币种分裂, 即挖上侧链条的人们任何上面的记账人, 下侧同理, 长此以往, 两条链条就分家了.(一个很典型的案例是 ETH 与 ETC).

很遗憾, 还有大问题, 因为币种分家后, 只有协议发生了改变, 而每个账户的公钥 / 私钥都没有变化, 这会导致本来只想被囊括在上侧链条中的交易被重复囊括在下侧链条中. 这就又会可能导致各种各样的双花攻击.

有一种简单的处理方法即在两侧分家后的交易中都加上 chain ID 这个变量, 这能使得两侧的链条均得知一个交易是应当在哪一个链条上进行的.

10.2 Soft Fork

10.2.1 软分叉概念

所谓 软分叉(Soft Fork) 指的是旧节点能够兼容新的更新改动. 举一个假设, 比如 降低比特币区块大小上限 (注意, 这只是个例子, 现实中没有发生过)

为什么叫做软分叉, 我们还是假设多数人认可这个更新, 因此从算力投票的角度, 必定是小区块产生的速率更快一些(链条更长一些).

此时, 由于旧节点认可新链条 , 根据最长合法链原则, 它会自动抛弃当前链条, 而转向新的小区块链条.

这代表着, 如果它坚持不更新, 它的收益会受损(它挖出的所有大区块都白挖了), 而整个区块链仍然会长时间保持一条最长合法链, 也就代表着此时的分支是 暂时的 .

10.2.2 软分叉实例

一种比较典型的案例即对某些目前协议中未曾规定的域赋予一些新的含义(规则). 比如我们之前提到的 Coinbase Transaction 中的 Coinbase 域(详见5.2.2).

我们提及过, Coinbase 域内有一部分可能被作为 extra nonce , 但 Coinbase 域很大, 只用作这个多少有点浪费, 因此有人曾经提及, 剩余的部分可以用于存储 UTXO 集合的根哈希值, 这就是一个典型的软分叉.(但最终未被实行)

比特币中一个很著名的软分叉加入的功能, 就是 Pay to Script Hash 功能(详见 9.2.2 和 9.3)的加入, 这个脚本功能在最初的 BTC 中是不存在的, 但后续通过软分叉进行加入.

另一个十分著名的通过软分叉加入的功能被称作 隔离见证(SegWit / Segregated Witness) , 这个功能使得每一笔交易中的 签名(Signature) 和 交易本身的信息(Tx Information) 被隔离开来, 将所有的签名相关信息放入 Coinbase Transaction 中. 这个更新 显著降低了交易平均大小 , 使得比特币的交易效率大幅提升.

Part11. BTC中的匿名性

所谓 匿名性(Anonymity) , 指的是一个人的身份在其进行某个事项时可以不被泄露, 进而他在现实中的身份不会公开, 也无法被攻击.

Anonymity describes situations where the acting person’s identity is unknown. The important idea here is that a person be non-identifiable, unreachable, or untrackable.

从这个角度来理解, 现金的匿名性其实是最好的, 因为当钱花出之后, 无人能够得知这张钱曾经经过你的手中. 当然, 现金的局限性也很高, 因为它不好管理, 不好存储.

BTC的匿名性体现在任何人只需要创建一个 < 公钥 , 私钥 > 对, 就可以成为一个用户, 而无需实名制. 但相对应的, 其账本是公开的.

现今社会中银行的匿名性体现在其账本不公开, 只有交易双方能得知这笔交易的存在, 但需要对一个中心管理机制实名.

11.1 输入地址 / 输出地址之间的关联

这里所说的输入地址 / 输出地址通常指的是一笔交易中输入货币的原账户与输出货币的目的账户. 我们通过本节的论述可以发现其中有一些特殊情况下, 二者是可以建立联系的.

我们假设一笔交易有四个账户

• 输入账户(Input Address): $ Add_1(spend \space 4 \space BTC), Add_2(spend \space 5 \space BTC)$
• 输出账户(Output Address): $ Add_3(receive \space 6 \space BTC), Add_4(receive \space 3 \space BTC) $

为什么需要有多个输出账户呢?

因为通常而言, 一个BTC账户上的钱很少能够等于商品的价格, 因此, 通常输入的BTC数量是要高于商品价格的, 至于剩余的BTC怎么处理, 则由支付方再额外提供一个 找零账户 , 将多余的BTC单独创建一个输出, 转到那个找零账户上.

我们考虑上面举的例子, 通常的情况下, 上面的情况都代表着:

• $ Add_3 $ 应当是收款方的账户, 而 $ Add_4 $ 应当是付款方的找零账户.(如果后者是收款方账户, 则无需两个付款账户一并付款)
• 某些情况, $ Add_1, Add_2 $ 这两个账户可能有关联, 甚至干脆属于同一个人.

显然, 通过这一个交易就能分析出一些 交易用户之间的关联信息 , 这本身就是对交易匿名性的一种破坏(更甚, 可以系统的分析大量的交易记录, 从而得到一些确定性较高的信息, 虽然这难度颇高).

11.2 与个人实际身份的关联

我们考虑, 当比特币一旦与现实生活中的某些行为产生关联, 比如大额法币 / 比特币的转入 / 转出时, 显然会引起司法部门的关注, 而由于最终都要置换为现实生活中有实际消费价值的法定货币, 因此这代表着个人肯定能被某些手段推测到的. 这从一定意义上讲, 也是对匿名性的一种破坏.

从这个角度上来讲, 参与比特币这个链条最久的, 比特币的发明者 中本聪 , 是保证自己匿名性最好的人, 因为他从始至终从未花费自己的任何比特币财产, 也就意味着他从始至终没有将自己的账户与任何现实生活中的行为产生任何关联.

上述两个章节, 主要目的在于说明比特币的匿名性并没有达到十全十美, 请各位读者不要有什么危险的想法(笑)

11.3 保证匿名性的手段

我们此前(6.1)提及过, 比特币是基于传统的TCP / IP协议进行协议设计的. 这就意味着, 要想增强其匿名性, 需要从应用层的协议设计入手.

至于为何不急于传统的传输层与网络层进行进一步工作, 这是因为传输层的TCP / IP协议的设计已经相对完备, 并且加密手段也已经比较完善, 这里不会将重点放在它上.

11.3.1 Coin Mixing

所谓Coin Mixing, 指的是 对一定量的货币进行多次操作(即使这些操作是不必要的), 以使得最终交易双方转出 / 收到的货币无法被溯源 的一种方式.

Coin mixers allow users to mix up transactions between different cryptocurrency addresses, so they become untraceable and cannot be followed back to the initial sender or receiver.

Coin Mixing这个功能通常以协议的方式被设计出来, 被广泛采用, 如各类货币交易所 / 虚拟货币钱包APP等.

当然, Coin Mixing本身是存在风险的, 因为这个操作本质上是一种货币的支出 / 收入, 因此如果参与者所选择的中介不值得相信, 则很容易造成严重的个人损失.

11.4 Zero-Knowledge Proof

In cryptography, a zero-knowledge proof or zero-knowledge protocol is a method by which one party (the prover) can prove to another party (the verifier) that a given statement is true, while avoiding conveying to the verifier any information beyond the mere fact of the statement’s truth.

通俗而言, 零知识证明 指的是 证明者向验证者证明一个陈述是正确的, 但又无需向验证者透露任何除了该陈述是正确的之外的任何信息 .

比特币采用的思想有点类似这里的思路, 在比特币中, 如果证明者A希望证明一个账户是自己的, 往往需要发布一个 自己私钥的签名 , 而其余的验证者可以通过该签名能否与对应账户的公钥相匹配来验证 账户属于证明者A 这个命题是真实的.

这一整个过程中, 证明者A达成了 不将自己的私钥透露出去的同时, 也能够证明账户属于自己 的目的.

Part12. 总结 / 一些细碎的具体化工作

12.1 区块链究竟是如何存储的 / 哈希指针怎么实现的?

我们在此前的叙述中, 一直通过 哈希指针(Hash Pointer) 这个比较抽象的概念对区块链进行数据结构化工作, 但这个过程并不十分具体.

事实上, 在大部分全节点处, 一个个的区块被存储在 数据库 中, 存储形式是键值对, 即<key, value>形式(一个相当出名的数据库被称作Level DB).

• key: 区块的哈希值
• value: 区块内容(Block Header / Block Body)

在实际系统中, 所谓的哈希指针, 就是一个哈希值, 因为可以通过哈希值来借由全节点查找到相应的区块内容, 这也就变相实现了指针的功能.

12.2 共享账户的实现方式?

曾经有一些人采用过一种风险相当大的方式进行共享账户, 即 私钥切割 , 每个人保管私钥中的其中一部分.

这是一种风险相当大的方式, 比特币的私钥采用SHA-256哈希算法, 有256位, 我们假设一人保管128位, 两个人的共享账户, 这意味着另一个人 破解这个私钥 的难度大大降低, 因为他只需要尝试 $ 2^{128} $ 种可能就可以了, 这远远小于比特币最初设计的 $ 2^{256} $ . 这个破解难度会随着合伙人增加而显著降低.

因此, 如果存在合伙人共享账户的情况, 请务必 使用多重签名(MultiSig) 的方式!

12.3 比特币中的有限共识

我们此前提及分布式系统共识时, 提及过CAP, 即一个共识系统是无法保证 一致性(Consistency) / 可用性(Availability) / 分区可用性(Partition tolerance) 同时满足的, 那比特币怎么还能通过共识的形式成立?

事实上, 比特币系统中实现的也是 有限共识 , 它并没有打破学术界的已知结论, 但它做到了在一些额外机制的参与下尽可能维护这个系统的持续运行. 一个典型的 有限共识 例子即分支攻击, 当分支攻击发生时, 原先已经被建立的共识也会被推翻.

我们对于区块链第一部分(Bitcoin)的概述就到这里.

再次对北京大学对应课程组表达感激与敬意!

希望本篇博文能对读者系统的了解区块链的原理有一定的作用, 同时也权当对于知识的记录, 以供再度查阅.

这篇博文就到这里~