本系列概率论博文基于Bilibili宋浩老师发布的概率论教学视频整理而来, 仅用作复习参考. 在此感谢宋浩老师的开源工作.
概率论与数理统计 Chap.2 随机变量及其分布
2.1 随机变量
首先要引入一个非常核心的概念, 这个概念贯穿着我们此后概率论内容的始终.
概念: 随机变量
对于一个样本空间 $ \Omega = {\omega_i} $ , 我们对其中每一个样本点 $ \omega_i $ 设置一个不同的实数 $ X(\omega) $ , 此时我们记这个 $ X $ 为一个随机变量.
随机变量通常用一个大写字母来进行标识.
需要读者理解这个定义, 这实质上是将一个 $ \geq 1 $ 维的样本空间, 转化到了一个 1维 的数轴上, 实际上代表了一种 映射关系 .
那我们引入这玩意有啥用呢? 当然是要用它表示事件求概率啊!
我们通常可以用以下式子来表示一个事件及其概率:
$$ \lbrace X \leq x \rbrace , P \lbrace X \leq x \rbrace $$
这里还请各位读者理解这个表示方式, 它有点像微积分里面的 变上限积分函数 . 这个 $ x $ 本身也是个变量, 但是在这个式子中, 它取到某一个特定的值时, 这个事件是能有一个准确的概率值的.
2.2 离散型随机变量及其分布律
刚刚说的随机变量既然是一种映射, 那它的取值自然分为 离散型 和 连续型 . 这一节先从离散型开始.
2.2.1 概率分布?
对于离散型而言, 其概率分布就是: $ P \lbrace X = x_k \rbrace = p_k , k = 1, 2, … $ .
其实就是随机变量取到每一个离散值的概率是多少. 它也通常使用表格来表示:
$$
\begin{array}{c|c|c|c|c}
X & x_1 & x_2 & x_3 & … \\
\hline
P & p_1 & p_2 & p_3 & …
\end{array}
$$
对于离散型的概率分布, 有这么几个要求:
- $ \lbrace X = x_1 \rbrace, \lbrace X = x_2 \rbrace, \lbrace X = x_3 \rbrace, … $ 是一个完备事件组.
- 就是所有样本点都包含在里面了
- $ p_k \geq 0 $
- 概率基本性质, 不说了
- $ \Sigma_{k = 1}^{\infty} = 1 $
- 就是所有样本点的概率加起来应该是1, 也就是不能有缺少的样本点.
- 也叫 归一性
下面会写一些常见的离散型概率分布.
2.2.2 0-1分布
这种是最好处理的, 本质上就是伯努利事件, 其样本空间仅有两个样本点, 因此我们将其抽象为 0, 1.
给出概率分布:
$$
\begin{array}{c|c|c}
X & 0 & 1 \\
\hline
P & 1-p & p
\end{array}
$$
或者我们用一个表达式来写它:
$$ P \lbrace X = k \rbrace = p^k (1-p)^{1-k} , k = 0, 1 $$
2.2.3 二项分布
二项分布实际上就是 n重伯努利实验 , $ P(A) = p $ , 我们引入随机变量X表示A发生的次数.
$$ P \lbrace X = k \rbrace = C_n^k p^k (1-p)^{n-k} , k = 0, 1, 2, …, n $$
我们将其记作: $ X \sim B(n, p) $
- n: 伯努利实验总次数
- p: 单次事件发生的概率
其实读者能看出来, 二项分布中 $ n = 1 $ 时, 就是 0-1分布 了.
这玩意也是肯定满足归一性的:
$ \Sigma_{k = 0}^{\infty} C_n^k p^k (1-p)^{n-k} = (p+(1-p))^n = 1 $
这个式子读者如果有疑惑可以去搜索 二项式展开 , 这里不费笔墨了.
2.2.4 泊松分布
泊松分布有点复杂, 我们先给定义:
$$ X \sim P \lbrace X = k \rbrace = \frac{\lambda^k}{k!} e^{- \lambda} , k = 0, 1, 2, … $$
我们记作 $ X \sim P(\lambda) $
这东西的归一性需要一个高数中比较重要的泰勒展开式: $ e^x = \Sigma_{k = 0}^{\infty} \frac{x^k}{k!} $
这个式子这里就不证明了, 读者忘记了可以自己搜一下.
有了这个式子, 我们推一下归一性:
$ \Sigma_{k = 0}^{\infty} \frac{\lambda^k}{k!} e^{- \lambda} = e^{- \lambda} \Sigma_{k = 0}^{\infty} \frac{\lambda^k}{k!} = e^{- \lambda} * e^{\lambda} = 1 $
泊松分布有一个非常重要的应用, 它能够用于近似实验量极大的二项分布:
设 $ X \sim B(n, p) , n \geq 100 , np \leq 10 $ , 则上述二项分布可以使用泊松分布 $ X \sim P(\lambda) , \lambda = np $ 来近似.
这样近似的目的显而易见, 当二项分布的 n 过大时, 会涉及到超大指数的幂运算, 而泊松分布能够极大程度上简化这一计算过程.
2.2.5 几何分布
我们还是先给定义:
$$ P \lbrace X = k \rbrace = (1-p)^{k-1} p , k = 1, 2, 3, … $$
我们记作 $ X \sim G(p) $
同样的, 我们推一下归一性:
$ \Sigma_{k = 1}^{\infty} (1-p)^{k-1} p = p \Sigma_{k = 1}^{\infty} (1-p)^{k-1} = p \frac{1}{1-(1-p)} = 1 $
几何分布针对的场景是这样:
一个事件A, 其发生的概率是p, 一直独立的重复这个实验直到A发生为止. X描述的是A发生时的实验总次数.
2.2.6 超几何分布
超几何分布针对的场景是这样:
两类共N个物体, 第一类 $ N_1 $ 个, 第二类 $ N_2 $ 个. 从中取出n个, 引入X表示从第一类中取出的物体个数.
$$ P \lbrace X = k \rbrace = \frac{ C_{N_1}^k C_{N_2}^{n-k} }{ C_N^n } , k = 0, 1, …, min \lbrace n, N_1 \rbrace $$
这其实就对应着我们的 不放回抽取 .
当然, 我们也会碰到一种很难办的情况, 就是N特别大, 并且 N >> n , 这种情况我们通常使用二项分布 $ X \sim B(N, \frac{N_1}{N_1 + N_2}) $ 来对超几何分布进行近似.
本质上就是在总实验量过大的时候, 用放回抽取来近似不放回抽取.
至于二项分布在这种数据量极大的情况下怎么算?
请移步刚刚的泊松分布.
2.3 随机变量的分布函数
2.3.1 分布函数的定义
先给出定义:
$$ F(x) = P \lbrace X \leq x \rbrace , x \in (- \infty, + \infty) $$
请读者明确两点:
- 这个函数的自变量是 $ x $ , 即理解为一个随机变量的 取值限值 .
- 这个函数的因变量是 一个概率 , 即 $ X $ 取到的值比 $ x $ 小这个事件的概率.
它的含义与微积分中变上限积分函数的感觉非常相似. 还请读者尽可能理解.
2.3.2 分布函数的性质
分布函数的性质还是比较重要的, 这里单拉出来开一小部分:
- $ 0 \leq F(x) \leq 1 $
- 因为分布函数的函数值是个概率嘛
- $ F(- \infty) = 0 , F(+ \infty) = 1 $
- 通过x取值范围得到的结论
- F(x)一定是一个 不减函数 .
- 理解上: x增加时, X能够取到的样本点一定是不减的, 那取到这些样本点的概率也一定是不减的.
- 证明上: $ F(x_2) - F(x_1) = P \lbrace X \leq x_2 \rbrace - P \lbrace X \leq x_1 \rbrace = P \lbrace x_1 < X \leq x_2 \rbrace $ , 显然这个值 $ \geq 0 $ , 得证.
- F(x)是一个 右连续函数
理解这些性质之后, 有仨比较常用的公式, 做题常用, 也比较好理解, 这里提一下:
- $ P \lbrace a < X \leq B \rbrace = F(b) - F(a) $
- $ P \lbrace X > a \rbrace = 1 - F(a) $
- $ P \lbrace X < a \rbrace = F(a) - P \lbrace X = a \rbrace $
2.4 连续型随机变量及其概率密度函数
连续型相比于离散型的区别在于其随机变量的取值, 它能取 一段区间内的全部实数 . 因此不是很好理解.
2.4.1 概率密度函数
我们先来捯饬一下这个概率密度函数是个啥意思:
设X为随机变量, 存在一个非负可积的函数 $ f(x) , f(x) \geq 0 $
并且 $ \forall a < b, P \lbrace a < X \leq b \rbrace = \int_a^b f(x) dx $
我们称这样的 $ f(x) $ 就是随机变量X的 概率密度函数 .
这玩意确实不好理解, 读者请先明确, 这玩意是将概率用一个 积分 的形式来给出的. 也可以粗略的理解成函数图像的线下面积.
这玩意有好几个性质:
- $ f(x) \geq 0 $
- 如果这玩意能小于0, 那线下面积就是负的了, 概率显然不可能为负数.
- $ \int_{- \infty}^{+ \infty} f(x) dx = 1 $
- 随机变量X取遍整个实数域的概率显然是1
- 取个别点的概率为0
- $ 0 \leq P \lbrace X = x_0 \rbrace \leq P \lbrace x_0 - \Delta x \leq X \leq x_0 \rbrace = \int_{x_0 - \Delta x}^{x_0} f(x) dx $
- 显然, 当 $ \Delta x \to 0 $ 时, 右式趋近于0. 因此得证.
- 也正是由于这个性质, 在连续型随机变量求概率时 , 这几个式子是没区别的: $ P \lbrace a \leq X \leq b \rbrace = P \lbrace a < X \leq b \rbrace = P \lbrace a \leq X < b \rbrace = P \lbrace a < X < b \rbrace $
- $ F(x) = P \lbrace - \infty < X \leq x \rbrace = \int_{- \infty}^x f(x)dx $
- 根据密度函数的定义来的
- 连续性随机变量的分布函数 $ F(x) = \int_{- \infty}^x f(x) dx $ 一定是个连续函数.
- 对 $ F(x) $ 的连续点, 有 $ F’(x) = f(x) $
- 积分的逆过程就是求导嘛
2.4.2 概率密度函数 Vs 连续性随机变量的分布函数
我们直接给一个表, 展示一下这俩玩意的区别:
$$
\begin{array}{c|c}
f(x) & F(x) \\
\hline
0 \leq f(x) & 0 \leq F(x) \leq 1 \\
\hline
\int_{- \infty}^{+ \infty} f(x) dx = 1 & F(x) = \int_{- \infty}^x f(x) dx \\
\hline
可积, 不一定连续 & 一定连续 \\
\hline
增减性无要求 & 一定是不减函数 \\
\end{array}
$$
接下来我们给几个比较常见的连续型随机变量分布.
2.4.3 均匀分布
算是连续型里面最简单的一个, 我们直接给概率密度函数:
$$
X \sim f(x) = \begin{cases}
\frac{1}{b-a} & a \leq x \leq b \\
0 & else
\end{cases}
$$
我们将这种情况记作: $ X \sim U[a, b] $ , 它通常用于描述 概率在整个区间内均匀分布 的情况.
$$
F(x) = \begin{cases}
0 & x<a \\
\frac{x-a}{b-a} & a \leq x < b \\
1 & b \leq x
\end{cases}
$$
读者如果像得到这个 $ F(x) $ 求个积分就可以了, 应该不算难.
2.4.4 指数分布
还是先给概率密度函数:
$$
X \sim f(x) = \begin{cases}
\lambda e^{- \lambda x} & x>0 \\
0 & x \leq 0
\end{cases}
$$
我们将这种情况记作 $ X \sim E(\lambda) $ , 常用来描述各种电子元件的使用寿命(越长概率越小).
$$
F(x) = \begin{cases}
0 & x\leq 0 \\
1 - e^{- \lambda x} & x > 0
\end{cases}
$$
指数分布有个特别重要的性质, 在一些电子产品, 以至于信息行业中都广泛应用, 即它的 无记忆性 .
给出公式是这样的:
$$
\begin{align*}
\because & X \sim E(\lambda) , s>0, t>0 \\
\therefore & P \lbrace X>t \rbrace = P \lbrace X>s+t | X>s \rbrace
\end{align*}
$$
这玩意是啥意思呢? 我们翻译一下:
你的电子产品的使用寿命如果严格服从指数分布, 那么: 你刚拿到它能用t天不损坏的概率, 与你过一段时间拿到它能够再用t天不损坏的概率是相等的!
2.4.5 正态分布
老样子, 先给概率密度函数:
$$
X \sim f(x) = \frac{1}{\sqrt{2 \pi } \sigma} e^{- \frac{(x- \mu)^2}{2 \sigma^2}} , - \infty < x < + \infty
$$
我们将其记作 $ X \sim N(\mu, \sigma^2) $ , 这里的 $ \sigma > 0 $
那这玩意的分布密度函数:
$$
F(x) = \frac{1}{\sqrt{2 \pi } \sigma } \int_{- \infty}^x e^{- \frac{(x- \mu)^2}{2 \sigma^2}} dx, - \infty < x < + \infty
$$
这玩意如果想证明归一性需要用到微积分中的一个公式:
$ \int_{- \infty}^{+ \infty} e^{x^2} dx = \sqrt{\pi} $
这个公式读者想知道怎么证明应该可以上网搜, 挺多的.
有这个公式之后应该就好整了, 凑个微分就行, 在这就不详细说了.
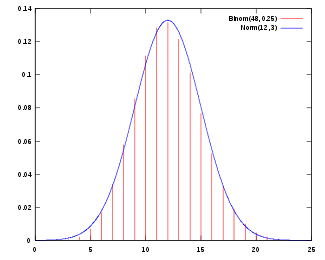
了解完这个, 我们来看一下正态分布的曲线, 这也是为啥它这么重要:
正态分布是一个以 $ x = \mu $ 为对称轴的 钟形曲线 .
长这样: ( $ \mu = 12 , \sigma = 3 $ )
这玩意着实比较有特点:
- $ x < \mu $ , 函数增, $ x > \mu $ , 函数减.
- $ \mu $ 只能影响函数的对称轴(左右移动)
- 最大值 $ x = \mu $ , $ y = \frac{1}{\sqrt{2 \pi } \sigma } $
- 又由于这个函数的积分值(线下面积)恒为1, 因此:
- $ \sigma $ 越大, 最大值越小, 取值越分散, 曲线越胖
- $ \sigma $ 越小, 最大值越大, 取值越集中, 曲线越瘦
2.4.6 标准正态分布
标准正态分布是正态分布的一种特殊情况:
$$
x \sim \phi(x) = \frac{1}{\sqrt{2 \pi }} e^{- \frac{x^2}{2}} , - \infty < x < + \infty
$$
记作 $ X \sim N(0, 1) $ , 其分布函数记作 $ \Phi(x) $
根据我们上面的结论, 能得到:
- 关于y轴对称 ( $ \phi(-x) = \phi(x) $ )
- $ \Phi(-x) = 1 - \Phi(x) $
- $ \Phi(0) = \frac{1}{2} $
- $ P \lbrace | X | \leq x \rbrace = \Phi(x) - \Phi(-x) = 2 \Phi(x) - 1 $
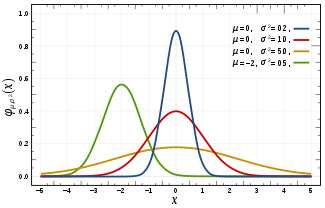
上图中的红线其实就是 标准正态分布 .
有这么标准的一条曲线, 我们能不能把所有正态分布都放在这条曲线上进行操作?
当然是可以滴.
定理如下:
$ X \sim N(\mu, \sigma^2) , f(x), F(x) $
则:
- $ f(x) = \frac{1}{\sigma} \phi(\frac{x- \mu }{\sigma}) $
- $ F(x) = \Phi(\frac{x- \mu }{\sigma}) $
有了这俩玩意, 我们就能算任意正态分布的 $ f(x), F(x) $ 了(只要知道 $ \mu , \sigma $ )
这个公式还有个更快捷的方式:
定理2:
对于 $ X \sim N(\mu, \sigma^2) , f(x), F(x) $ , 令 $ Y = \frac{x - \mu}{\sigma} $ , 则 $ Y \sim N(0, 1) $
因此:
$ P \lbrace a \leq X \leq b \rbrace = P \lbrace \frac{a - \mu}{\sigma} \leq \frac{x - \mu}{\sigma} \leq \frac{b - \mu}{\sigma} \rbrace = \Phi(\frac{b - \mu}{\sigma}) - \Phi(\frac{a - \mu}{\sigma}) $
这个玩意叫做 正态分布的标准化 .
除此之外, 还有个小结论, 读者想自己算一下也可以, 直接记住也行:
$ X \sim N(\mu, \sigma^2) $ ,
则:
X落在 $ | x - \mu | \leq \sigma $ 的范围内的概率为 0.6826;
X落在 $ | x - \mu | \leq 2 \sigma $ 的范围内的概率为 0.9544;
X落在 $ | x - \mu | \leq 3 \sigma $ 的范围内的概率为 0.9974;
可以通过这个结论记住这个 $ 3 \sigma $ 原则, 即正态分布几乎不会落在距离 $ \mu $ $ 3 \sigma $ 的范围外.
2.5 随机变量函数的分布
这里的 随机变量函数 指的是通过我们上面学过的几种典型的随机变量 构造出的新随机变量 .
2.5.1 离散型随机变量函数
非常简单, 离散型只有几个取值点对吧, 只需要将对应的取值点按照给出的函数操作即可.
给个例子: $ Y = 2X $
$$
\begin{array}{c|c|c|c}
X & 1 & 2 & 3 \\
\hline
Y & 2 & 4 & 6 \\
\hline
P & 0.3 & 0.3 & 0.4
\end{array}
$$
2.5.2 连续型随机变量函数
这种情况是最麻烦的, 因为往往涉及到函数的转换操作.
通常有两种解法:
- 通过 $ f(x) $ 求出分布函数 $ F_Y(y) $ , 随后 $ F_Y(y) $ 对 y 求导得到概率密度函数
- 通过 $ Y = G(X) $ 反解出 $ X = G^{-1}(Y) $ , 从而把 $ P \lbrace Y \leq y \rbrace $ 转化为 $ P \lbrace X \leq G’(y) \rbrace $ , 再通过讨论y的范围进行积分计算.
- 通过 $ f(x) $ 求出概率密度函数 $ f_Y(y) $ , 随后 $ f_Y(y) $ 对 y 积分得到分布函数
- 同样的 , 将 $ P \lbrace Y \leq y \rbrace $ 转化为 $ P \lbrace X \leq G^{-1}(y) \rbrace $ , 也就是 $ F_Y(y) = F_X(G^{-1}(y)) $
- 等式两侧同时对 $ y $ 求导, 得到 $ f_Y(y) = f_X(G^{-1}(y)) * G^{-1}(y)’ $ , 得到Y的概率密度函数
- 积分即可.
通过如上的步骤, 有这么两个结论要记一下:
对于均匀分布: $ X \sim U[a, b] , Y = cX + d $ .
$ Y \sim U[ac + d, bc + d] $
对于正态分布: $ X \sim N(\mu, \sigma^2) , Y = aX + b $
$ Y \sim N(a \mu + b, a^2 \sigma^2) $
当然, 上面只是非常简要的结论, 真正到比较复杂的函数变换时, 还是要照着此前的两种解法老老实实的干…
本章的内容就到这里了, 主要是关于随机变量的一些概念上的明晰, 以及几种重要的概率分布需要读者了解.
这篇博文就到这里~