写在前面：本课程会着重于半导体器件、逻辑代数以及逻辑门的学习，达到基本能够进行组合电路，时序电路以及运放（运算与放大）电路的识别、设计等操作。

数字逻辑基础

1. 计数体制

1.1 数制

我们将日常生活中由低位数向高位进位的规则称为 数制 。

在数字系统中，常用的数制包括：

• 十进制（Decimal）
• 二进制（Binary）
• 八进制（Octal）
• 十六进制（Hexadecimal）

它们分别表示逢几进一。

1.2 进制的转换

其他进制 -> 十进制

按权相加：将非十进制的各位权重乘以对应位的权重，再相加。
如：(10011.011)₂ -> (?)₁₀
其计算过程为：1 * 2⁴ + 1 * 2¹ + 1 * 2⁰ + 1 * 2^-2 + 1 * 2^-3

十进制 -> 其他进制

一般会将十进制的整数部分与小数部分分别转换并相加。
整数部分采用 除基取余法 ，小数部分采用 乘基取整法 。
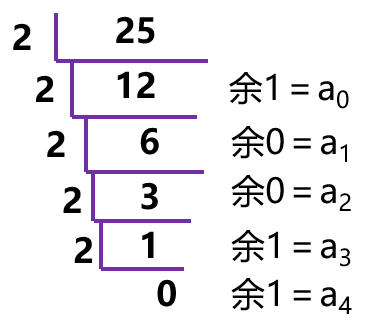
如：(25.25)₁₀ -> (?)₂
整数25部分：

小数0.25部分：

其他进制之间的互相转换

• 二进制 -> 八进制 / 十六进制：
  通常可以采用三位 / 四位二进制转为一位八进制 / 十六进制的方法进行快速转化

• 八进制 / 十六进制 -> 二进制：
  通常可以采用一位八进制 / 十六进制转为三位 / 四位二进制的方法进行快速转化

注：上述方法运用时从小数点开始往左 / 右进行转化，别忘记高位补0

2. 编码

由于在计算机内，处理、存储、传输的都是二进制数据，因此将外界信息通过二进制进行表示这一过程就显得尤为重要，这一过程被称为 编码

常见的编码有：

• BCD码
• ASCⅡ

BCD编码

利用四位二进制数来表示一位十进制数的过程被称为 BCD编码

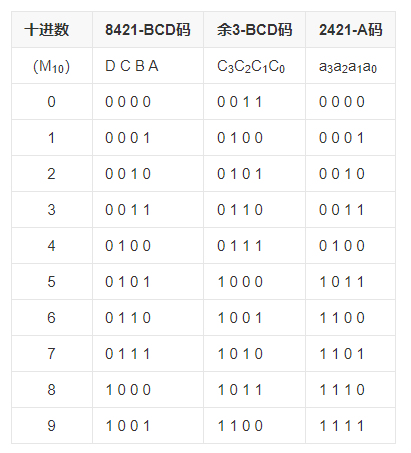
常用的BCD编码有：

• 8421码
• 余3码
• 2421码

其中8421码尤为常用，其名称代表着各个位次上二进制数字的权值

ASCⅡ

ASCⅡ（American National Standard Code for Information Interchange）用于通过八位二进制数来表示生活中常用的数字与符号，其中低七位用于表示，最高一位用于奇偶校验。

具体图片烦请读者自行上网搜索。

3. 逻辑代数基础

与现实中不尽相同，计算机由于采用二进制，因此其逻辑判断也仅有两种状态，即1（真）与0（假），在数字系统中，我们又常常将电位与真假相关联，即高电位（也称高电平）表示1，低电位（也称低电平）表示0。

3.1 基本逻辑运算与基本逻辑门

与运算

与运算 表示参与某一事件的全部条件都为真时，该事件才能发生。

或运算

或运算 表示参与某一事件的某一条件为真时，该事件就能发生。

非运算

非运算 表示将某一事件原本的真值倒置，1变0，0变1。

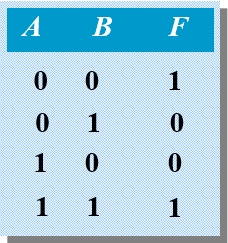
同或运算

同或运算 表示参与某一事件的两个条件相同时，该事件才能发生。

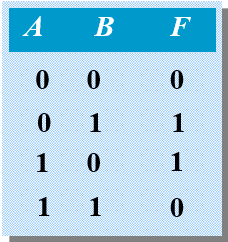
异或运算

异或运算 表示参与某一事件的两个条件不同时，该事件才能发生。

3.2 常用化简公式

数电中的化简方式繁多，这里给出一些常用的公式与定律，仅供参考
（有卡诺图谁用公式啊）

• 摩根定律 ：$\overline{\text{A * B}}$ = $\overline{\text{A}}$ + $\overline{\text{B}}$
  注：该公式来源于 反演率 ，即将公式中所有的乘加互换，01互换，原变量反变量互换，就可以得到原逻辑函数的反函数
• 吸收率 ：A * (A + B) = A
• 对偶规则 ：若两个逻辑函数相等，则它们的对偶式也对应相等。（对偶式的写法与摩根定律反演率相同）

3.3 逻辑函数的表示

逻辑函数通常有以下五种表达方式：

• 真值表
• 逻辑表达式
• 逻辑图
• 波形图
• 卡诺图

这其中，在手动化简时，以卡诺图最为常用：
具体表示为一个表格，表格横坐标与纵坐标均表示一个或多个逻辑变量，在相应的最小项处标记0 / 1表示假 / 真，而后利用偶数对画圈法将所有的1都圈起来，根据圈写出逻辑表达式。

这里举个例子：
假如m0, m1, m12, m13, m15, m14均为1，其他项均为0，则m0, m1为一组，表示为：$\overline{\text{A}}$ * $\overline{\text{B}}$ * $\overline{\text{C}}$ 。而剩余四个为一组，表示为： A * B
整体表达式为：
（$\overline{\text{A}}$ * $\overline{\text{B}}$ * $\overline{\text{C}}$ ）+ （A * B）

这篇博文就到这里~