发布日期: 2024-07-04

更新日期: 2024-07-28

文章字数: 5.5k

Blockchain(2)

在本节中, 我们主要会针对 以太坊 这一另一个主要的加密货币进行说明.
仍然需要写在前面, 本文主要基于《区块链技术与应用》(北京大学肖臻教授) 的课程进行笔记整理与内容扩展, 文中除开视频内容外,也会涉及到一些博主自己的思考, 烦请读者理性看待. 在此也附上视频链接(https://www.bilibili.com/video/BV1Vt411X7JF?p=1&vd_source=4565edcb254cb6582d6382ac80011294), 有了他们的工作, 才能让区块链这一技术为更多人所知.
在此对肖臻教授以及北京大学相应课程组表达诚挚的敬意与感激!

Part.1 以太坊概述

以太坊(Ethereum) 对于比特币中出现的各种问题进行了更为针对性的改进, 包括但不限于 出块时间 / 谜题设计 / 共识协议 等等方面.

与此同时, 以太坊相对于比特币的最显著的该进, 在于 智能合约(Smart Contract) 的提出.

为什么要提出智能合约?

在BTC时代, BTC实现的最重要的成就是它达成了一个真正的 去中心化的货币政策(Decentralized Currency) , 比特币通过技术手段取代了一部分本该通过政府来保证的公信力; 人们看到了BTC的成功, 并希望将这种去中心化的思路推而广之(If we can decentralize currency, what else can we decentralize?), 以太坊在此基础上设计出了 去中心化的合约设计(Decentralized Contract) , 智能合约类似地通过技术手段, 取代了一部分原本应当由司法机关来保证的合约公信力.

Part.2 账户

2.1 以太坊中的账户模型

在比特币中, 账户仅仅是一个 <公钥, 私钥>对, 这意味着账户十分容易创建, 而且一个人可以很轻松地拥有多个账户. 同时一个账户中的余额需要通过查询 UTXO 才能真正得知(比特币是基于交易的账本: Transaction based ledger).

这种方法的好处在于隐私性的保护较强, 但同时也意味着交易过程中有了很多麻烦 ~~(用户自己可能都说不清我有多少钱, 更别提别人了)~~

典型的麻烦在于, 当一个用户(我们后文称之为用户1)希望向另一个人转账时, 他必须将他此前参与交易的输出(相当于此前转到自己一个账户上的钱)全部花出去(这代表着假设交易金额与输出金额不等, 则用户1必须单独再创建一个账户来接受找零, 详情请见上一个章节的11.1). 显然, 这相当的别扭.

在以太坊中, 采用了传统的 基于账户的模型(Account Based Ledger) , 这代表着系统上必须显式记录每个账户上有几个ETH. 此时要检测交易是否合法, 则只需检查转账账户上是否有足够的金额即可, 无需像比特币一般说明金额的具体来源.

这种模型对 双花攻击(Double Spending Attack) 有天然的防御作用, 因为交易必定需要扣除余额.

重放攻击(Replay Attack)

重放攻击指的是 收款人 在收到付款人的交易请求后, 正常接收这个交易, 但在后续过程中再次向交易网络中重新转发这个交易, 达到让自己多次收款的目的.

以太坊采用的账户模型对于重放攻击是需要单独进行防护的, 以太坊对每个账户单独设置了一个域nonce, 表示 这个账户的总交易数 , 如果收款方重放该交易, 会由于总交易数nonce相同而被无恶意的节点拒绝.

2.2 账户的分类

以太坊中含有两类账户:

Externally owned Account: 也称外部账户(或普通账户), 这种账户很类似比特币中的账户, 利用公私钥控制. 这种账户的状态值包括:
- Balance: 账户余额
- nonce: 账户交易总数(类似计数器)
Smart contract Accound: 也称合约账户, 合约账户不是通过公私钥进行控制的, 同时合约账户也不能主动发起交易, 这代表着它涉及的所有交易都是由外部发起的, 同时每调用一次合约账户会导致其存储内的某些特定状态值发生变化. 其状态值包括:
- Balance
- nonce
- code: 代码
- storage: 存储(其他额外的状态值)

后续我们会进一步对上面的各种状态进行说明, 读者在这里不必过于纠结它们的用途.

2.3 为什么是账户模型 ?

以太坊为什么要改用 账户模型 ?

当然, 交易更方便, 速度更快是理由之一. 但更本质的原因, 在于以太坊创建的系统是 智能合约系统 , 而合约的根本, 在于交易双方必须要 保持稳定 , 想比特币那样收一笔钱换一个地方的做法在合约中显然是行不通的.

Part.3 数据结构

3.1 状态树

谈完了模型, 我们来说说实现方式.

我们需要实现的, 是一个从账户地址(Address)到账户状态(State)的有效映射. 在以太坊中, 账户地址是一个160bit的二进制数, 我们一般将其表示为40个16进制数.

我们先来排除一个错误选项: Merkle Tree 能当此任吗?

答案是否定的. 有两个原因.

首先, 我们如果通过哈希的方式将 以太坊中所有的账户 组织在同一颗 Merkle Tree 中, 会导致任何账户信息更新的操作的开销都十分庞大. 因为 Merkle Tree 这玩意通过哈希指针连接双亲结点与孩子节点, 因此牵一发而动全身, 而所有账户一起组成的 Merkle Tree , 实在是太大了.

其次, 比特币中能够采用 Merkle Tree 的原因在于 Merkle Tree 仅存在于一个区块中, 它仅仅组织一个区块内的交易排列, 以及包含的交易信息. 这个过程有一个很明确的 共识源头 即获取到记账权的那个节点(挖到这个区块的矿工). 但如果以太坊的账户管理仍然套用 Merkle Tree , 这个共识源头就不好找了, 意味着让所有节点形成共识的难度也过高.

因此, 我们排除利用 Merkle Tree 来存储账户信息的想法.

3.1.1 Trie(字典树)

我们揭晓以太坊的数据结构之前, 先来说说这个简化的数据结构: Trie(字典树) .

In computer science, a trie, also called digital tree or prefix tree, is a type of k-ary search tree, a tree data structure used for locating specific keys from within a set.

这种数据结构, 就是专门用于通过关键字来进行数据查找的. 通过例子也能够看出, 一般而言这种查找是通过字符串进行的.

提到字符串, 我们想一想能跟以太坊建立起什么联系?

前面提及到的, 以太坊的地址是160bit的二进制数, 而我们通常使用 40位16进制数 来表示. 这意味着, 如果使用Trie进行存储, 算上字符串结束符, 每个节点最多能够衍生出 17个分支 , 树的深度固定为 41.

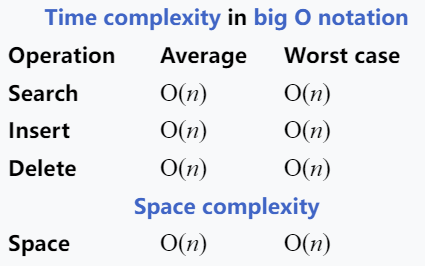
Trie相比于Merkle Tree有什么好处?

上图中, 我们发现对于Trie, 搜索, 插入, 删除的时间复杂度都取决于字符长度, 而我们这里字符长必定是40. 显然, 相比于 Merkle Tree , Trie的各种操作效率可高太多了.

此外, 不论怎么打乱重排给入这颗 Trie, 最后构造出的Trie应当是一样的, 因为Trie是根据字符串本身进行插入操作的.

最后, 当这棵Trie需要更新时, 也不用访问其他分支, 不用遍历, 只需要根据给定地址访问指定分支即可, 即更新局部性控制的很好.

按理来说, Trie已经挺不错了, 但人们还是不满足, 人们觉得查找效率还是不够高.

对于上面的例子而言, 像 inn 这样的节点, 我还需要找三次才能找到它, 但它过程中没有什么分支, 那我能不能再度简化查找过程?

3.1.2 Patricia Tree(路径压缩前缀树 / 压缩前缀树)

Patricia Tree(Trie) , 也称路径压缩前缀树(字典树) , 是一种在传统字典树上对于单一路径进行进一步压缩的前缀树.

我们给出一个路径压缩的例子:

这样的好处在于: 树的深度显著减少了, 查找花费的时间更短了.

当然, 我们也需要明确, 路径压缩也意味着需要插入新单词的时候可能涉及到更复杂的 路径拆分操作 . 同时, 路径压缩只在数中插入键值分布比较分散的时候比较有效.(举例而言, 单词很长, 但总数并不多时), 当键值分布过于密集, 意味着可供压缩的路径较少, 则这种方法与传统字典树的效率差的并不多.

当然, 我们这里只需要考虑这160位地址, 即以太坊的地址总空间有 $ 2^{160} $ 次方这么大, 这是个天文数字, 我们的地址分布也因此及其稀疏. 因此采用路径压缩的方式的效果还是很不错的.

3.1.3 Merkle Patricia Tree(梅克尔路径压缩前缀树 / MPT)

我们继续向下, 现在我们成功的将这棵树压缩了一下, 理论上讲, 相比于此前的Trie, 采用Patricia Tree的树应该要精简许多, 那我们现在想想, 是否能将这棵树中的指针换成哈希指针呢?

当然可以, 这正是我们现在的主流做法. 我们最终可以将这棵树的根哈希值放入块头中, 用于保证整棵树没有被改变过, 同时, 要查找时, 我们可以利用Patricia Tree的特点, 通过前缀快速查找到一个节点是否存在.

读者读到这里可能会有疑问, 为什么之前Merkle Tree行不通, 现在就突然能成了?

我们思考我们上面这一系列流程干了些啥: 我们通过用户地址将每个账户进行了标识, 明确了要利用 字典树 的性质来进行查找, 这保证了状态树查找时的效率; 我们通过 路径压缩 , 在以太坊的用户地址分布及其分散的情况下, 极大程度上降低了树的深度和宽度, 这保证了树的大小不会太大; 我们利用 梅克尔树 的性质, 在指针上附加哈希值, 保证了树的不易篡改性.

因此, 事实上, Merkle Patricia Tree 是一种对 数据完整性 / 存储效率 / 查找效率 的平衡.

我们此前在以太坊的账户章节(2.2)中提及: 以太坊中存在两种账户, 普通账户 与 合约账户 . 事实上, 这两种账户需要存储的内容不尽相同, 因此用于存储它们账户状态的 MPT 结构自然也不同.
那这两种账户是怎么同步在全球的以太坊树中的呢? 答案是, 通过我们前面提到的账户地址.
全球的以太坊树是一颗大的MPT, 它其中的每个叶子节点都是一个账户的地址, 这个地址指向一颗小的MPT. 至于指向的是哪种MPT, 则根据账户本身的类型来决定(普通账户MPT / 合约账户MPT).
因此, 以太坊的MPT存储方式是分级存储的.

这也代表着修改的便利性, 当一个新区块被添加到区块链中, 需要 根据全球MPT找到区块内所有涉及到的账户MPT -> 修改对应的账户MPT 即可完成操作, 其他不涉及到的内容可以原封不动的搬过来.

相对应的, 在修改账户MPT时, 也只需要寻找到需要修改的变量, 修改之, 即可. 不需要整体重新建立.

3.1.4 Roll Back

我们会发现, 以太坊中每个区块都要维护一个全局状态树和很多的个人账户状态树, 这看起来好像很浪费? 为什么要这么设计?

不同于比特币10分钟的出块时间, 以太坊的出块时间非常快, 接近15s. 这意味着很有可能产生临时性的分叉, 直到某一个分叉胜出后, 其余分叉才被判定为 Orphan Block 而被淘汰. 现在我们想一想, 当某一个节点所正在接受的分支被淘汰了, 它们应当怎样转到正确的分支上?

他们需要先进行 回滚操作(Roll Back) , 随后才能沿着新链条继续下去, 但这个回滚操作应当如何进行?

这就用到了此前区块中保存的状态树, 由于以太坊智能合约的存在, 以太坊的交易类型极大的复杂化, 因此必须要保存此前区块的全部状态树以保证 回滚的准确性 .

3.1.5 Key-Value Pair

我们倒腾了这么半天, 状态树这东西到底里面是什么?

说说白了, 就是一个个的键值对.

对于账户状态树而言, 其键(Key) 就是账户地址的哈希(那个160位二进制数的哈希值, 采用Keccak-256加密算法), 值(Value) 就是该地址对应的账户对象(包括余额 / nonce / {代码哈希} / {存储根} , 利用RLP进行字符数组序列化操作)

RLP(Recursive Length Prefix) 是一种数据编码方法, 目的在于将任意结构的数据进行高效的序列化 / 反序列化操作, 具体序列化完成后体现为字节序列.

状态树中的共享节点

状态树中这种键值对的存储方式决定了以太坊的账户状态树的运作模式, 即只有账户状态被改变时, 才需要新建一个分支来存储它, 在本区块中 某个账户状态未发生变化 , 则在本区块的状态树中, 可以原封不动的将上个区块的键值对搬过来(相当于还是指向同一个账户即可).

这代表着其实以太坊的状态树中, 存在大量的共享节点, 也使得存储效率得以提升.

3.2 交易树 / 收据树

在上一节中, 我们了解了以太坊中的状态树, 而这一节, 我们需要了解两个较小的树 交易树 & 收据树 , 之所以说它们比较小, 是因为相比于状态树, 这两棵树只会将 某个区块内涉及到的交易 / 收据进行存储 , 而不会像状态树一样存储所有账户的状态.

但从数据结构上来说, 交易树和收据树本质上还是 MPT . 不过与状态树不同的是, 交易树 / 收据树 无法共享节点 .

3.3 Bloom Filter

3.3.1 Bloom Filter 的定义

Bloom Filter 是一种用于 快速查找 的数据结构, 从理论上来讲, 它可以用于快速查找一个元素是否在一个集合中.

其原理是, 算法首先产生一个数组 , 将这个数组整体 初始化置0 , 此后对于集合中的每个元素都运用 一个或多个哈希函数 , 将其映射到数组中的 多个位置 , 对于这些位置, 置1 .

当需要查找某个元素是否在上文中的集合中时, 只需要将这个元素运用相同的哈希函数, 映射到数组的对应位置, 并 检查这些位置是否都为1 即可.

这样做的好处在于检查者不需要得知一个集合中全部的元素, 而只需要知道这个集合映射过后的一个指定数组就可以进行查找操作, 这是对空间复杂度与时间复杂度的极大优化.

A Bloom filter is a space-efficient probabilistic data structure, conceived by Burton Howard Bloom in 1970, that is used to test whether an element is a member of a set. False positive matches are possible, but false negatives are not – in other words, a query returns either “possibly in set” or “definitely not in set”.

但Bloom Filter也有缺陷, 由于其采用了哈希算法, 因此 哈希碰撞 就显得不可避免. 当要查询的元素(这个元素本身 并不在集合内 )进行哈希过后, 产生的哈希值与集合中某个元素完全一致时(即产生了哈希碰撞), 此时就会出现误判现象. 因此, Bloom Filter只能代表 元素一定不在集合中 或 元素很可能在集合中 这两种结果.

这也就是为何Bloom Filter可能采用一组而非一个哈希函数, 一组哈希函数的哈希碰撞率是很低的, 能够有效降低这种数据结构查找时的误判率.

除此以外, Bloom Filter还 无法删除元素 , 如果我们草率地将要删除的元素对应的数组位改为0, 如果集合中有同样映射到此位置上的元素, 则这个元素就会被误删.

3.3.2 Bloom Filter in Ethereum?

Bloom Filter 在以太坊中主要被用于区块头中的 交易树根 和 收据树根 的快速查找, 以此来提升以太坊的查询效率.

由于以太坊的交易复杂性, 导致频繁的查找某一 特定类型 的交易的操作是十分常见的. 因此以太坊引入了Bloom Filter数据结构, 以达到快速查找的目的.

以太坊中, 每个交易自身都有一个Bloom Filter(就是我们前面说的数组), 而区块头中的交易树根和收据树根则是所有交易Bloom Filter的并集 . 当查询者需要查找对应类型的交易时, 会先根据指定类型查找区块头中的交易树根 / 收据树根; 如果找到了, 则再遍历区块中所有交易的Bloom Filter, 查找区块中是否有指定类型的交易.

注意, 由于Bloom Filter的误判可能性, 因此可能会出现查询区块头时匹配成功, 但区块中其实并没有指定类型交易的情况(出现了哈希碰撞).

Part.4 共识协议: Ghost

我们进入Ghost之前, 先考虑一下为什么比特币的挖矿协议用在以太坊上不可行?

在比特币中, 出现分叉后, 会根据后续挖矿的进度来决定最长合法链, 而被抛弃的链条(Orphan Block)上面的一切改动都会被作废, 包括区块记账权获得者的铸币奖励. 这是因为比特币的出块时间非常长, 有10分钟, 因此这种临时性的分叉不会对整个网络造成太大影响.

但在以太坊中, 出块时间只有15秒, 分叉的可能性大大提高. 如果还像以前一样, 分叉上的交易 / 奖励全部作废, 这就代表着节点费劲千辛万苦挖出来的区块可能是个无用功, 这是不可接受的. 因此, 以太坊引入 Ghost 协议来解决这个问题.

需要明确的是, Ghost协议并不是以太坊的发明, 以太坊在初版Ghost的基础上进行了一定的修改, 并应用于自己的系统中.

4.1 Ghost Protocol

在此前 以太坊的出块奖励还未归零 时, Ghost规定, 如果当前区块链中存在 叔块(Uncle Block, 即比特币中的 Orphan Block) , 并且这个叔块 还未被主链接受(即此前还没有主链上的节点引用这个叔块), 则主链上的节点(Nephew Block)可以在其挖出区块的头部将这个叔块包含进来, 即将叔块的哈希值放入自己的区块头中. 这被称为 引用叔块 , 相对应的, 引用叔块的矿工会得到一笔引用奖励, 通常为 $ \frac{1}{32} $ 的常规区块奖励.

一个 Nephow Block 最多可以包括 2 个叔块.

需要明确的是, 以太坊中的叔块并不是严谨上的叔叔. 它在技术上的定义细节如下:

Uncle Block 的出块时间必须比 Nephew Block 的出块时间早.
Uncle Block 的高度必须比 Nephew Block 低 6个区块 以内.
Uncle Block 不能是 Nephew Block 的 直接祖先区块 .

必须满足这三点, 一个区块才能被视作叔块, 并被包含在Nephew Block中.

与此同时, 被引用的叔块的记账人也能够获得一笔补偿费, 在当时, 这个补偿费是 $ \frac{8-differce \space height}{8} $ 的常规区块奖励, 其中 $ difference \space height = nephewHeight - uncleHeight $ , 即叔块和当前块的高度差, 这样设计代表 以太坊鼓励出现分叉后立即合并 , 因为合并越早, 得到的奖励越多.