Chap.5 安全检索技术

5.1 安全检索的概念以及必要性

云存储使得数据的所有权和管理权相互分离, 因此如何保证云数据的安全性成为了问题.
通用的方法是用户首先使用安全的加密机制(各种加密算法)对数据进行加密后上传至云服务器. 随后需要本地取用则只需要将密文下载至本地即可.

这个过程有其问题, 因为它要求客户端需要有较大的存储空间和计算能力, 反而减弱了云存储的优势.

5.1.1 密文检索

密文检索(Searchable Encryption, SE) 的概念是:

云存储系统在密文场景下对用户数据进行检索，然后将满足检索条件的密文数据返回给用户。

显然, 云服务器在这个过程中收到的是密文, 因此无法获得用户的敏感数据和查询条件. 这保护了数据机密性和查询机密性.
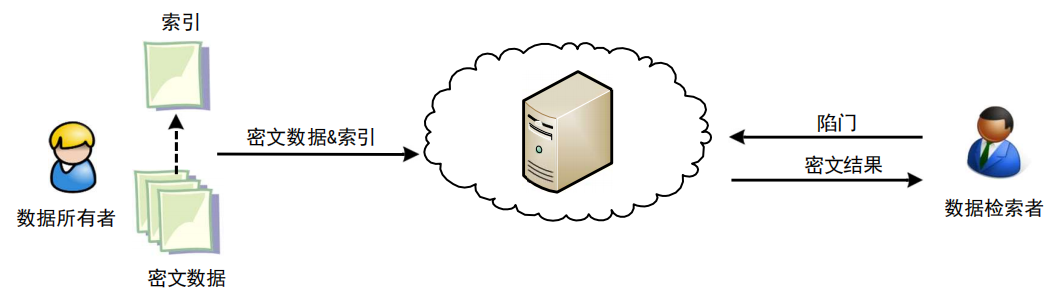
通常这个过程涉及到三种角色:

• 数据所有者: 即敏感数据的拥有者, 上传密文数据并生成索引
• 数据检索者: 查询请求的发起者, 生成陷门并发送给服务器
• 服务器: 为二者提供服务, 由云服务提供商进行管理和维护, 通过内置定义好的匹配算法将来自检索者的陷门和所有者的索引相匹配, 并返回给检索者以密文数据.

根据应用场景的不同, 可以分为两大类:

• 对称密文检索(SSE): 只有数据所有者拥有密钥, 也只有数据所有者可以提交数据 / 生成陷门. 这种情况下数据所有者和数据查询者是一个人.
• 非对称密文检索(ASE): 任何能够获取到数据检索者公钥的用户都能够提交数据, 但只有数据检索者能够生成陷门.

同时根据数据类型的不同, 又可以将检索分为两类:

• 关键词检索(主要搜索字符型数据)
• 区间检索(对数值型数据进行范围查询)

5.2 早期安全检索技术

5.2.1 PIR技术

PIR(Private Information Retrieval)主要针对公开数据库, 目标是允许用户不向服务器暴露意图的前提下得到自己需要的内容.

这个方案比较复杂, 我们用一个例子来解释:
我们假设有矩阵:

$$
\begin{pmatrix}
1 & 2 & 3 & 4 \\
5 & 6 & 7 & 8 \\
9 & 10 & 11 & 12 \\
13 & 14 & 15 & 16
\end{pmatrix}
$$

假设用户要查询一个 $ x_{3, 2} = 10 $ .
正常的思路是我直接给服务器发, 说我要查 $ x_{3, 2} $ , 但很可惜, 这样我们的意图就被服务器看的一清二楚.

因此我们想了个法子, 把我们的意图隐藏一下:
先把我们要查的东西转成一串二进制数: $ x_{3, 2} \to x_{i_1, i_2} = x_{0010, 0100} $ , 1在第几位就是坐标.
随后我们生成两个 随机数 : $ \delta = 1001, \tau = 0010 $ .
我们要让随机数跟我们要查询的坐标有点联系, 所以我们计算: $ \delta_1 = \delta \oplus i_1 = 1011, \tau_1 = \tau \oplus i_2 = 0110 $

我们要向多个服务器发送请求(假设每个服务器存储的信息是相同的, 也就是上面的这个矩阵).
怎么发呢:

• 向第一个服务器发送 $ \delta, \tau $
• 向第二个服务器发送 $ \delta, \tau_1 $
• 向第三个服务器发送 $ \delta_1, \tau $
• 向第四个服务器发送 $ \delta_1, \tau_1 $

服务器收到这些请求之后会返回结果: $ \oplus_{\delta(j_1) = 1, \tau(j_2) = 1} x_{j_1, j_2} $ . 这是个贼抽象的式子, 啥意思呢: 就是把第一个数为1的地方当作横坐标, 第二个数为1的地方当作纵坐标, 组合一下之后全部异或, 再返回这个值.

举个例子, 比如我们向第一个服务器发的值是 $ \delta, \tau = 1001, 0010 $ , 也就是取出 $ x_{1, 3} $ 和 $ x_{4, 3} $ 来异或, 返回这个结果: $ 3 \oplus 15 = 12 $

我们照着这个规律得到全部的返回结果:

• 第一个服务器返回12
• 第二个服务器返回0
• 第三个服务器返回7
• 第四个服务器返回1

随后客户端把这四个数再做异或, 就能得到正确结果 $ 12 \oplus 0 \oplus 7 \oplus 1 = 10 $

注意
上述方案是一个典型的4服务器PIR方案, 实际上, PIR服务器数量并不是固定的, 信息论上来讲, PIR的服务器只需要 $ \geq 2 $ 即可.
对于查询数字(也就是发给服务器数字)的长度, 通常是 $ \sqrt{n} $ , 其中n是数据总量.

5.2.2 ORAM技术

ORAM认为整个服务器的存储介质都是不安全的, 因此数据是加密的, 并且要向服务器隐藏读写两种操作.
ORAM实际上的思路是将一次操作转化为多次操作(其中可能混杂着不相关的操作), 这使得服务器完全不知道你的目的是什么, 即使它都知道你干了什么.

这种方式的技术实现难度要远高于PIR, 因此本博客中就不详细叙述了, 有兴趣的读者自行了解吧. (我也不会.jpg)

5.3 对称密文检索技术

我们上文提过, 对称密文检索技术即 数据所有者与数据检索者 是同一方. 这适用于大部分第三方存储.

通常一个对称密文检索技术包含四部分算法:

• Setup: 数据所有者执行, 生成用于加密数据 / 索引的密钥
• BuildIndex: 数据所有者执行, 根据数据内容建立索引
• GenTrapDoor: 数据检索者执行, 生成陷门(搜索凭证)
• Search: 服务器执行, 将接收到的陷门和本地索引进行比对, 引入预设计算过程并返回密文结果.

5.3.1 基于全文扫描的方案

该方案的核心思想是对明文进行分组加密, 并将加密后的结果与一个伪随机串异或得到索引.

这种方案的缺点是可以看出来的, 它依靠对全文进行顺序扫描来进行检索, 因此最坏情况下(比如关键词在全文最后), 它需要检索完整篇文章才能够返回对应的密文, 效率较低.

5.3.2 基于文档-关键词索引的方案

核心思路是为每篇文档建立单独的索引, 服务器搜索时遍历全部索引即可.

检索时间复杂度与文档数目成正比.

5.3.3 基于布隆过滤器的密文关键词检索方案

首先了解一下布隆过滤器是什么, 这是一个用于快速判断某一个元素是否位于一个集合中的方法.

构造位数组BF, 长度为m.
设待检索集合 $ S = [x_1, x_2, …, x_n] $
选取k个哈希函数 $ h_1, h_2, …, h_k $
分别对集合中的每个元素用这k个哈希函数进行运算, 并将运算出的哈希值记录下来, 将位数组对应位置的值记为1.

当需要判断y是否在S中时, 同样进行k次哈希运算, 如果得到的结果对应的位数组位置均为1, 则认为这个元素在S中.

5.3.4 基于关键词-文档的方案

相当于倒过来, 原先都是为文档单独创建索引, 这里为某个关键词单独创建索引. 这使得查找效率大大提升.

这种方式实现起来实在复杂, 就不整理了.

5.4 非对称密文检索技术

非对称密文我们在开始的时候也提及了, 是一个数据拥有者和检索者并非同一人的情形. 但其算法结构其实跟对称密文检索技术是相似的:

• Setup: 数据所有者执行, 生成用于加密数据 / 索引的密钥
• BuildIndex: 数据所有者执行, 根据数据内容建立索引
• GenTrapDoor: 数据检索者执行, 生成陷门(搜索凭证)
• Search: 服务器执行, 将接收到的陷门和本地索引进行比对, 引入预设计算过程并返回密文结果.

5.5 密文区间检索技术

提过哈, 就是涉及到数值区间问题的时候.

5.5.1 基于桶式索引的方法

对属性值域进行分桶, 为各桶分配一个唯一的标识(也就是记录的索引).
查询时, 用户将与检索区间相交的标识集发给服务器, 服务器将这些分桶全部发回给客户端.

显然, 这种方式分桶完全是服务器的活, 因此返回的数据很可能包括大量的冗余数据.

5.5.2 基于B+树的传统加密技术方案

这种方案为数据构造B+树, 服务器会将密文节点返回给用户, 用户解密后自行判断, 并通知服务器下一个节点位置.

这种方案需要客户端与服务器多轮交互.

还有一种基于矩阵加密的方式, 比较复杂, 这里不提了.

5.5.3 基于等值检索的方案

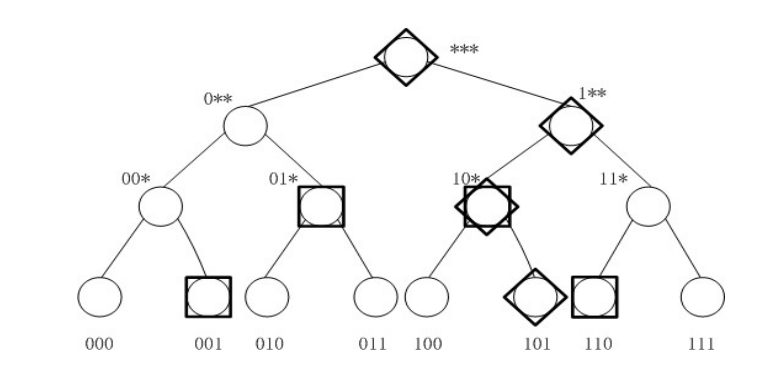
这种方案的想法是把区间检索转化为关键词检索. 将每个属性值当作一个关键词, 然后对区间内部的属性值进行枚举, 再对每个枚举结果进行关键词搜索即可.

不适用于检索区间精度高或者检索区间较大的情况 .

比如我要查询 [1, 6], 那只需要枚举 [001, 01*, 10*, 110] 这四种方案即可.