Chap.6 安全处理技术
6.1 安全处理技术的概念及必要性
6.1.1 同态加密的概念
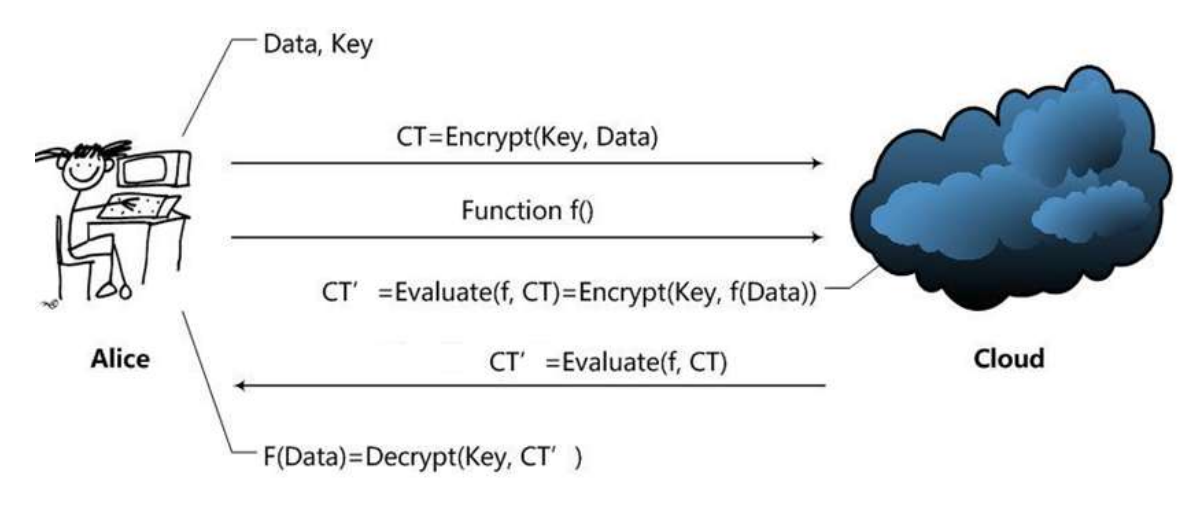
安全处理技术解决的情况是: 用户想让第三方帮自己处理数据, 但同时又不希望数据本身遭到泄露.
这种情况下, 同态加密 就应运而生, 其大致分为三步:
- 用户在客户端本地加密, 随后将数据发送给云
- 云端对加密过后的数据进行运算处理, 但本身由于数据加密无法得到有效信息
- 处理完成后用户拿回处理结果, 基于密钥对数据进行解密, 得到运算完毕后的数据.
相信大伙都看出来了, 这东西想要达成的目的是: 对密文数据进行计算, 解密后能得到与对明文数据直接计算相同的结果 .
6.1.2 同态加密的方案过程
同态加密通常有四个需要实现的过程:
- KeyGen: 生成公私钥(sk, pk)
- Encrypt: 输入明文m, 加密得到密文 $ c = Encrypt(pk, m) $
- Decrypt: 输入私钥sk和密文c, 得到明文 $ m = Decrypt(sk, c) $
- Evaluate: 输入公钥pk和布尔电路C以及密文 $ \vec{c} $ , 得到 $ c^* = Evaluate(pk, C, \vec{c}) $
需要给出三个定义, 供读者区分:
- 一个方案的正确性: 即对于一个方案 $ \epsilon = (KeyGen, Encrypt, Decrypt, Evaluate) $ 而言, 如果对于这个方案内给出的布尔电路, 加密完运算再解密的结果与直接运算的结果相同, 则说明这个方案是正确的.
- 同态加密: 即给出的加解密算法对于一类布尔电路 $ \mathbb{C} $ 是正确的
- 全同态加密(最严格的定义): 给出的加解密算法对于所有的布尔电路都是正确的
6.2 同态加密的基础: 语义安全性
6.2.1 可忽略函数
我们首先需要引入一个概念叫 可忽略函数 :
一个函数 $ f(n) $ 是可忽略的, 代表着对于任何正整数c, 都存在足够大的 $ n_0 $ 使得当 $ n > n_0 $ 时都有:
$$ f(n) < \frac{1}{n^c} $$
这代表着, $ f(n) $ 是随着安全参数n变大而变得非常小的函数, 小到比任何多项式的倒数都要小.
我们一般把一个可忽略函数记为 $ \mu(n) $ .
这玩意有啥用呢?
通常用它来衡量攻击者能够攻击成功的概率.
6.2.2 挑战游戏与语义安全性
通常语义安全性会与一个挑战游戏相关, 我们称之为 $ Game_{A, \epsilon}(\lambda) $ :
- 挑战者生成公私钥(pk, sk), 将公钥pk发给敌手A
- 敌手A得到pk, 生成两段等长的消息 $ m_0, m_1 $
- 挑战者选择第0条或者第1条消息加密发回给A, 选择记为 $ b $
- A去猜测这个加密过后的消息是来自 $ m_0 $ 还是 $ m_1 $ 的, 输出 $ b’ $
- 如果猜对了, 则游戏成功, 否则游戏失败.
我们说的 语义安全性 意思是:
攻击者无法从我们给出的密文中得到非常显著的, 能有助于其猜到加密原文的助益. 即:
$$ | Pr[b’ = b] - \frac{1}{2} | \leq \mu(n) $$
满足了语义安全性, 我们能确保计算方无法根据我们提交的密文得到我们的明文到底是什么.
6.3 计算结果的正确性
解决了机密性, 我们现在需要着眼于正确性, 对啊, 怎么能保证对面算出来的东西没错呢?
这个问题通常有几种方式:
- 复制: 让多个服务器都干这个活, 取最多的相同结果
- 审计: 我自己算一部分, 对比结果
- 可验证计算: 基于密码学的方法
6.3.1 两方参与的可验证计算
可验证计算的本质其实是将两方抽象化了:
- 验证方: 计算能力弱, 但可信(客户端)
- 证明方: 计算能力强, 但不可信(服务器)
实际上, 其思路就是: 我要让服务器给我一个简易的证明过程, 使得我能很方便的确认你给我的结果是没错的.
我们用数学语言写一下:
验证方给定输入 $ x $ 和函数(运算) $ f $ , 证明者期望产生一个输出 $ y $ 以及相应的证明 $ p $ , 证明内容就是 $ y = f(x) $ . 验证者要用这个证明 $ p $ 来验证整个计算的正确性.
当然, 这里涉及到两个前提, 都很好理解:
- 合理性条件: 就是说, 你产生的这个证明 $ p $ , 效率必须要高于我自己算一遍 $ f(x) $ .
(对啊, 要不然我为啥不自己算捏) - 安全性条件: 就是说, 你为造一个 $ y^* , p^* $ , 使得用 $ p^* $ 来证明 $ y^* = f(x) $ 是不可行的.(说白了就是你给我的这个证明必须是有效真实的, 要不然就没意义了)
读者可能很好奇了, 哎, 这种玩意真存在吗?
还真有, 因为我们要搞的是证明工作, 因此可以用概率的知识.
有种玩意叫 概率检测证明(PCP, Probabilistically Checkable Proof) , 就是证明者为了验证某一结论的合法性而给出的一个串, 其性质是验证者只需要查看PCP的一个常数常量就可以检测PCP的合法性.
6.3.2 比特承诺
比特承诺想干的事情比较简单:
A发送给B一个证明(承诺), 承诺的内容是一个比特:
- A在打开这个承诺之前, B无法得知里面是什么
- A也不能篡改这个打开的承诺
因此比特承诺也就自然的被分为了两个阶段:
- 承诺阶段: A选择一个比特(0, 1), 并将能够代表这个比特的消息c发给B
- 打开阶段: A把打开这个承诺的方案d以及承诺文b交给B, B打开c, 并验证里面是不是b.
需要满足的两个性质也比较好理解, 就是我们之前说的那两条:
- 隐藏性: 在承诺阶段,接收方无法知道被承诺的值
- 绑定性: 承诺方在揭示时无法更改自己原本承诺的值
上面这两种我们都比较熟悉(也许不熟悉? 请了解加密算法以及哈希后如闪电般归来!)
下面还有一种比较高级的, 它基于二次剩余.
回顾一下二次剩余, 定义如下:
对于X, d, p, 如果存在:
$$ X^2 \equiv d \space mod \space p $$
则称d是模p的二次剩余.
比如1, 2, 4就是模7的二次剩余.
现在我们来讲这个高级的法子奥:
基于Goldwasser-Micali的比特承诺
- 承诺阶段:
- 令 $ n = pq $ , 其中 $ p, q $ 都是大素数. 选择模n的 非二次剩余m .
- A随机选择 $ r \in Z_n^* , b \in \lbrace 0, 1 \rbrace $
- 计算 $ y = f(r, b) = m^b r^2 \space mod \space n $
- 打开阶段:
- A只需要揭示b, r即可
- B验证是否成立即可
6.3.3 交互证明
这个东西的本质是在用概率的方式来向他人证明我 有能力解决某个问题 / 有某个知识 .
这个例子很好的说明了交互证明的思想.
并能够引出我们之后想说的: 零知识证明(Zero Knowledge Proof)
6.3.4 零知识证明
零知识证明想解决什么问题呢?
即A向B证明我能解决某个问题, 但是B只能得到A的证明过程, 而自己仍然无法解出这道难题.
其必须具有的性质如下:
- 完备性: 证明者能够在多项式时间内提供证明过程
- 合法性: 验证者能够在多项式时间内跑完这个证明过程, 并确认其正确性
- 零知识特性: 证明过程不会暴露证明者所拥有的知识
显然, 这个零知识其实很难做到, 毕竟我们需要提供证明方案对吧.
- 完美零知识: 我提供的证明, 就算敌手的算力无穷无尽, 也无法通过我的这个证明得到任何有助于这个难题的信息
- 统计零知识: 我提供的证明, 确实与解决这个难题的方法微弱相关, 但是任何算力有限的敌手(多项式敌手)都无法通过这个证明来得到解题信息
6.4 安全多方计算
解决的是多个数据所有者在互不信任的条件下进行的协同计算.
6.4.1 Sharmir门限方案
秘密即构造一个k-1次多项式P(意味着只需要k个点就应该能够重现这个多项式), 而秘密通常被编码成这个多项式的一个点(截距, P(0))
$$ P(x) = S + a_1 x + a_2 x^2 + \ldots + a_{k-1} x^{k-1} \pmod p $$
现在假设总共N个人, 需要至少凑齐k个人才能还原多项式, 得到秘密.
因此步骤如下:
- 秘密分发:
- 选择模数p
- 选择N个不大于p的数 $ x_1, x_2, …, x_{N} $ , 分别计算 $ P(x_1), P(x_2), …, P(x_{N}) $
- 分发给N个人 $ (x_i, P(x_i)) $
- 秘密重构:
- 相当于集齐k个人, 就可以求出这个多项式, 并得到秘密.
这里重构多项式可以用拉格朗日插值法直接得到P(0):
$$ P(x) = \sum_{j=1}^{k} y_j \prod_{m=1, m \neq j}^{k} \frac{x - x_m}{x_j - x_m} \pmod p $$
当然, 如果多项式次数比较小, 也是可以直接解方程先解出多项式, 再求值.
6.4.2 混淆电路
这个情景是 A B 希望一块计算一个函数(可以看作是一个逻辑门), 即 $ f(x, y) = x \ AND \ y $
但是A不希望B知道我输入了什么, B也不希望A知道我输入了什么.
因此可以这样做:
这个过程中一定有一个 构造方 , 假设是A :
- 为自己的输入生成两个密钥 $ k_{0x}, k_{1x} $
- 为对方的输入生成两个密钥 $ k_{0y}, k_{1y} $
- 为输出生成两个密钥 $ k_{0z}, k_{1z} $
然后构造一个混淆真值表: 就是把这个
$$
\begin{array}{c|c|c}
A & B & A \land B \\
\hline
0 & 0 & 0 \\
\hline
0 & 1 & 0 \\
\hline
1 & 0 & 0 \\
\hline
1 & 1 & 1
\end{array}
$$
变成这个:
$$
\begin{align*}
E_{k_{0x}}(E_{k_{0y}}(k_{0z})) \\
E_{k_{1x}}(E_{k_{0y}}(k_{0z})) \\
E_{k_{0x}}(E_{k_{1y}}(k_{0z})) \\
E_{k_{1x}}(E_{k_{1y}}(k_{0z}))
\end{align*}
$$
随后:
- 把这四条打乱顺序发给B
- 把自己的选择对应的密钥(自己选0就发 $ k_{0x} $ ) , 发给B
- 把B的两个密钥( $ k_{0y}, k_{1y} $ )都发过去
B收到这些玩意, 拿A发过来的密钥以及自己的选择密钥来解密. 得到 $ k_{ _ z} $ , 再把这东西根据上面的翻译表得到结果, 把 结果(0 / 1) 发回给A.
A这时候就能知道最终的结果, 但A也不知道B的选择是啥.
注意
这个位置读者可能会很疑惑, 假如A选了1, 得到结果后不就自然能够得知B的选择了?
是的, 我们必须承认这种情况下A一定能够得到B的输出. 但还请读者注意, 这不是由于方案的问题, 这是函数的性质(因为我们选择的是一个简单的与门)
如果我们构造一个更加复杂的函数, (即通过我的选择和结果完全无法得知对方的选择时), 这种情况就不会发生.