Chap.3 加密防护的密码学基础
第二章的内容不是很重要, 被博主浓缩到了概述的1.3.0部分中, 这里我们直接进第三章.
3.1 密码学基本概念
3.1.1 密码体系五元组
这一部分其实对密码学有一些了解的读者会很熟悉, 我们简单过一下概念:
- 明文(plaintext): 通常用 $ M $ 标识明文空间, $ m \in M $ 表示其中一条明文
- 加密函数(encryption function): 通常用 $ E $ 表示, 以明文和密钥为输入, 密文为输出
- 密钥(key): 通常用 $ K $ 表示密钥空间, $ k \in K $ 表示其中一个密钥
- 密文(ciphertext): 通常用 $ C $ 表示密文空间, $ c \in C $ 表示其中一条密文
- 解密函数(decryption function): 通常用 $ D $ 表示, 以密文和解密密钥为输入, 明文为输出.
这就是密码系统中的五元组: <M, C, E, K, D> , 一般会满足以下要求:
- 系统是计算安全的(理论可破解, 实际破解花费时间过长, 无意义)
- 系统的保密性仅仅依赖于密钥(密码体制是公开的, 而使用者仅仅通过密钥保证安全, Kerckhoff原则)
- 便于实现 / 使用
密码系统遭受到的攻击一般分两类:
- 被动攻击: 对传输进行监听和监测.(窃听信道 / 流量分析)
- 主动攻击: 对信道中的数据进行篡改 / 伪造.(伪装, 重放, 篡改, 拒绝服务)
3.1.2 加密体制
当前的加密体制分以下两类:
- 对称加密: 加密和解密使用同一组密钥
- 非对称加密: 加密使用对方的公钥, 解密使用自己的私钥.
3.2 对称加密
3.2.1 对称加密的典型算法
DES(Data Encryption Standard): 是典型的分组加密算法. 所谓分组加密, 指的是将明文分为固定长度的一个分组, 随后对每个分组分别进行加密.
- 明文分组长度64比特(8字节), 密钥分组长度56比特(8字节, 每字节最低位是奇偶校验位), 输出为64比特(8字节).
- 有3DES的升级版本, 有两密钥 / 三密钥的加密方式.
- 两密钥加密方式原理如下: $ C = E_{k1}(D_{k2}(E_{k1}(M))) $ , 是一个 加密-解密-加密 的模式, 实际密钥区间为112位.
- 三密钥加密方式原理如下: $ C = E_{k3}(D_{k2}(E_{k1}(M))) $ , 同样是 加密-解密-加密 的模式, 实际密钥区间为168位.
3.2.2 对称加密模式
对称加密通常运用分组, 但怎么分组的加密方式有区别:
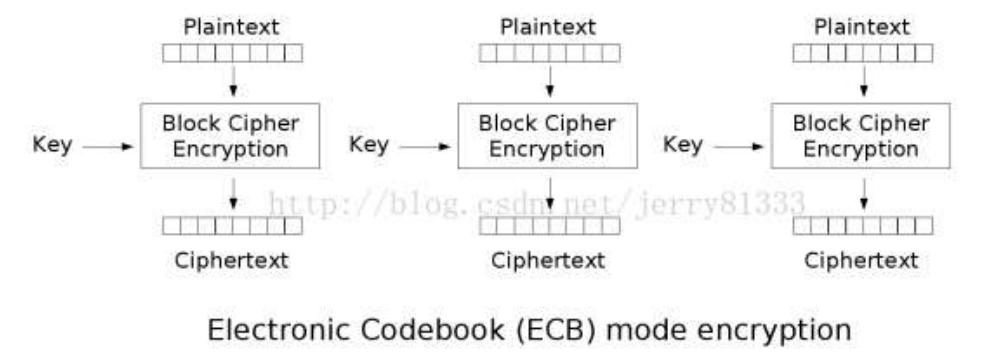
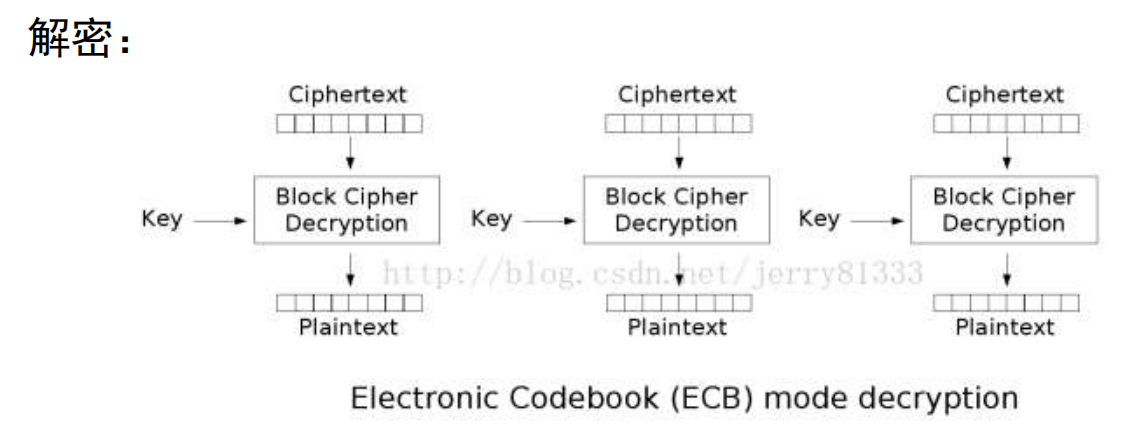
- 电码本模式(ECB)
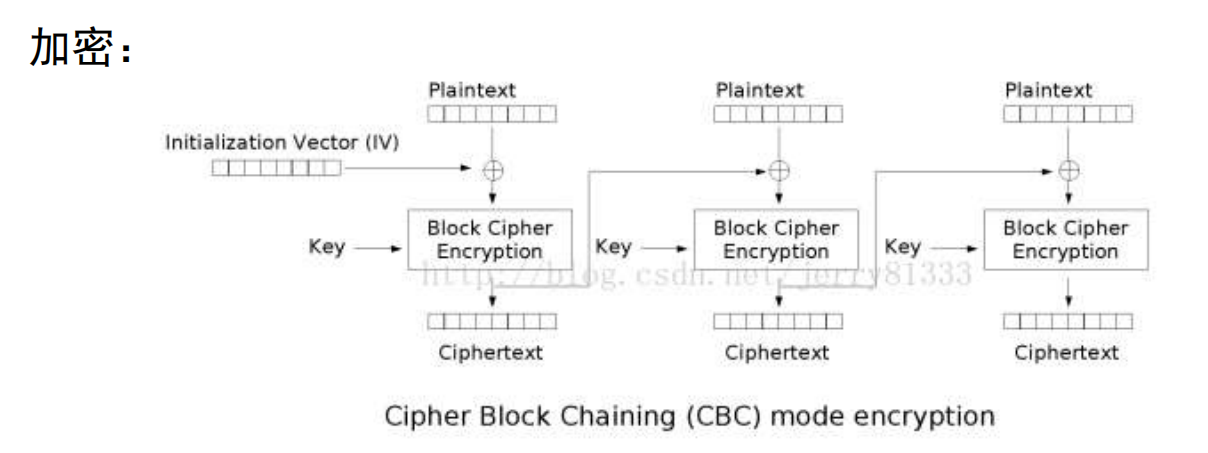
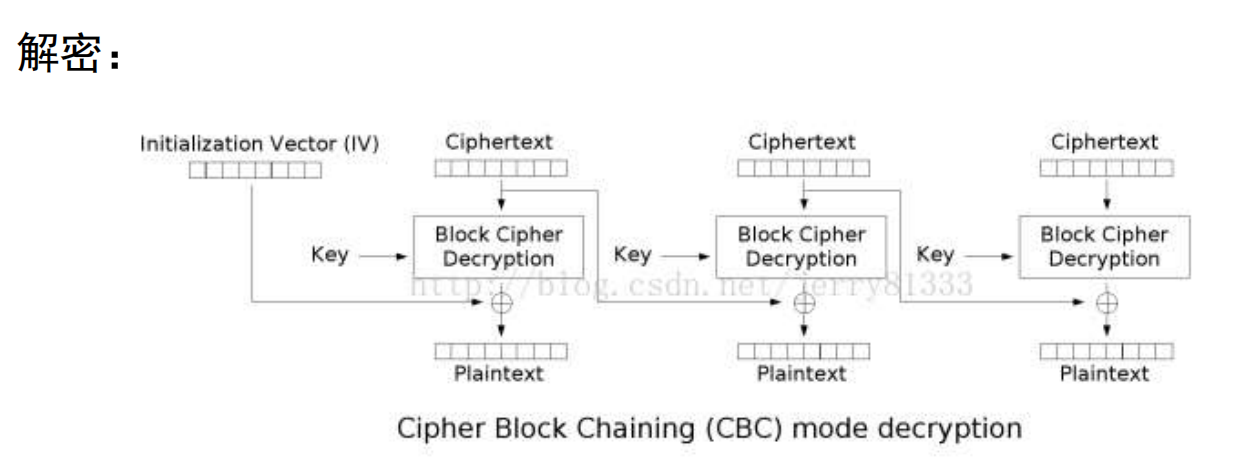
- 密文分组链接模式(CBC)
- 填充密码块链接模式(PCBC)
- 密文反馈模式(CFB)
- 输出反馈模式(OFB)
- 计数器模式(CRT)
电码本模式(ECB)是最简单的分组加密方式, 其直接将明文进行按照分组大小进行分组, 随后对每一组使用预先确认好的相同的密钥进行加密即可.
- 优势
- 简单, 各段数据之间互不影响, 利于 并行计算
- 密文块损坏时仅对应的明文损坏.
- 劣势
- 相同的明文块会得到相同的密文块, 不利于隐藏模式信息
- 加密消息块相互独立反而称为弱点(单独重放某一个密文块)
密文分组链接模式(CBC)尝试让后面的加密与前面建立联系, 会让每个明文块与前面的密文块异或之后再进行加密.(第一个明文块与初始向量 $ IV(Initialization \space Vector) $ 进行异或)
- 每一个分组都受到前面所有分组的影响
- 必须选择初始向量
- 不容易主动攻击(安全性比ECB强), 当密文块损坏(不管是由于攻击还是数据传输问题), 都会导致后续全部的密文无法正确解密.
- 串行加密, 无法并行化
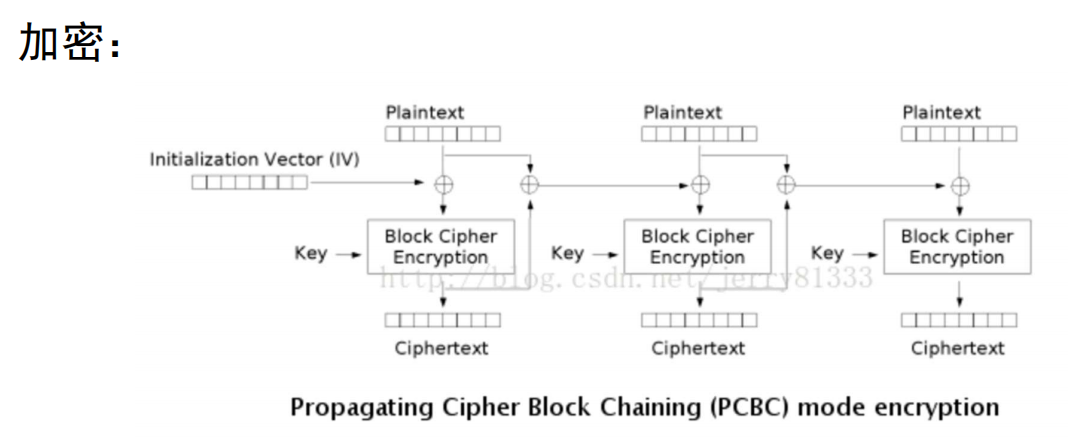
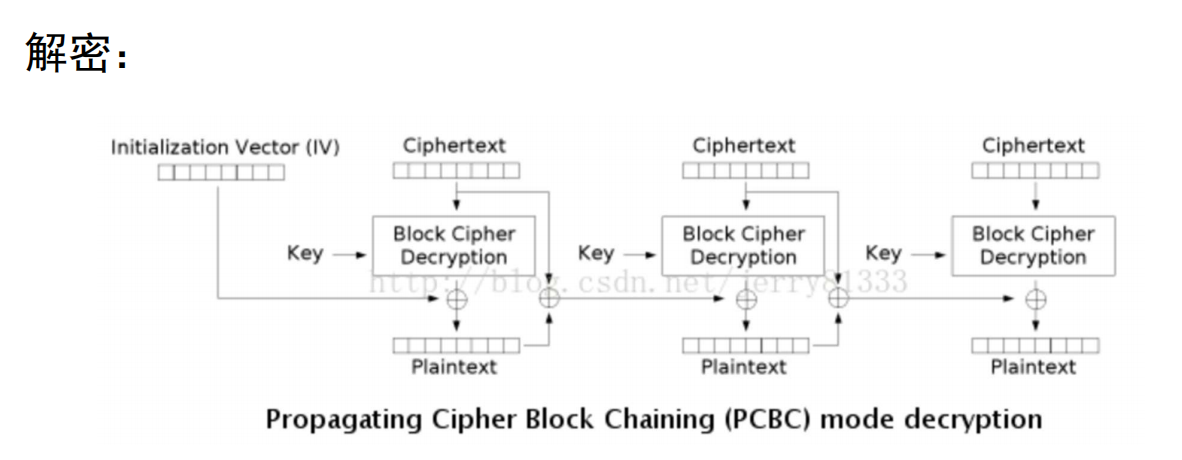
填充密码块链接模式(PCBC)尝试让前一个明文块和密文块都参与后续分组的加密, 每个分组加密前会异或上其前面那个分组 明文和密文的异或 .
- 密文中的微小更改会导致明文出现大部分错误
- 互换两个相邻的密文分组不会对后续的解密产生影响 .
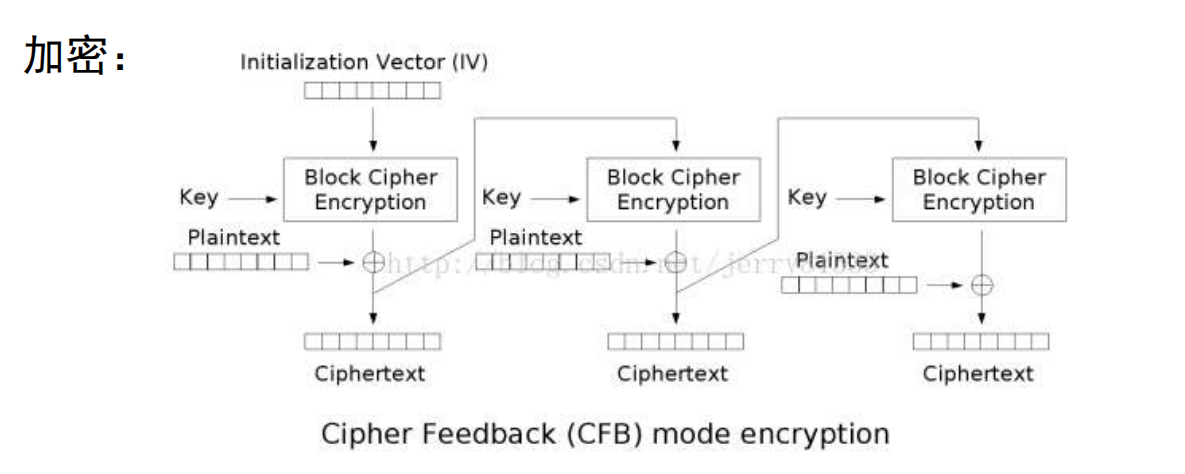
密文反馈模式(CFB)换了一种思路, 我不加密明文了, 我加密前面那个密文分组, 然后再跟明文异或以下得到当前分组的密文.
- 每一个区块的加密结果受之前所有区块内容的影响
- 明文的改变会影响后续的密文, 因此 加密不能并行化 , 但是 解密可以并行化
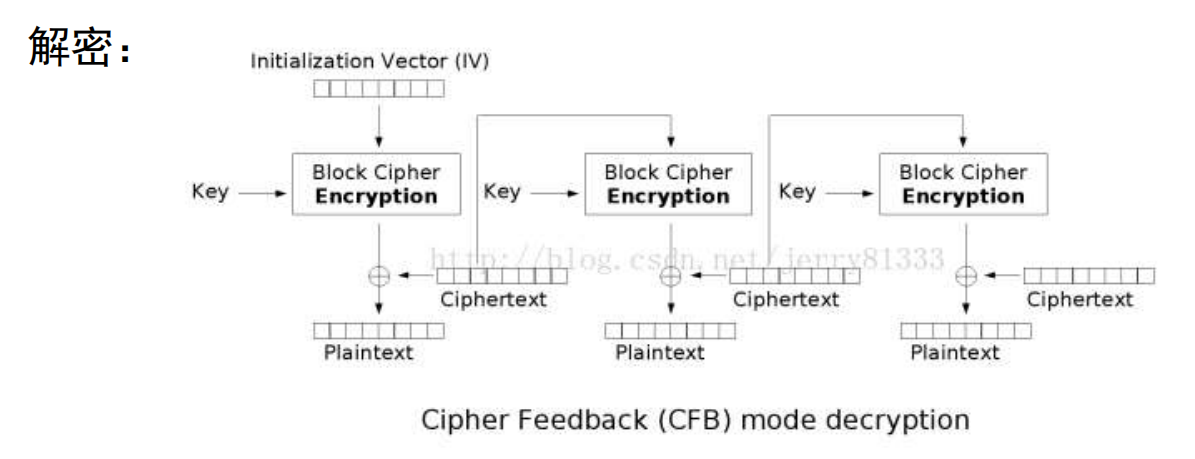
注意
注意看解密的图, 这个模式下全程不涉及到Decryption函数.
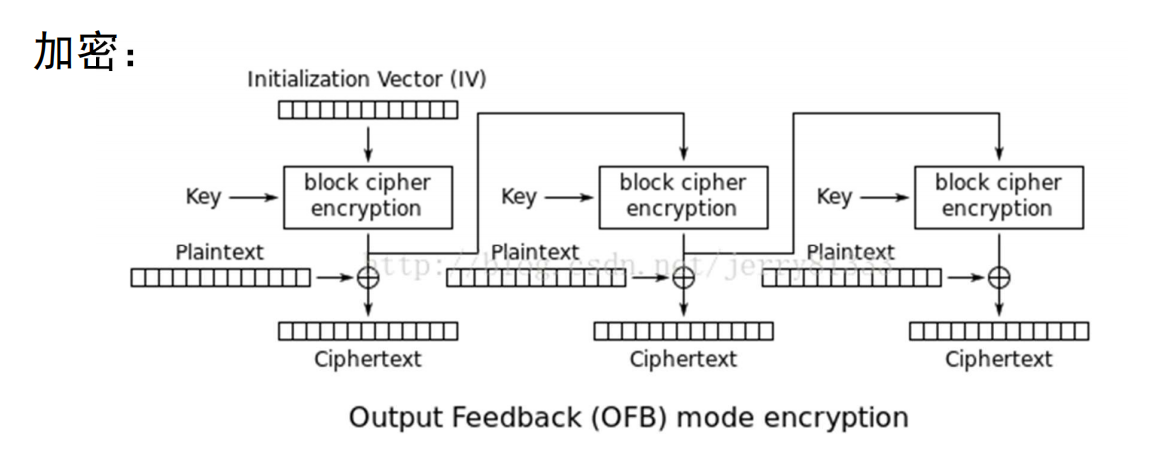
输出反馈模式(OFB)先用块加密器得到密钥流(Keystream), 随后再将密钥流跟明文异或得到密文.
- 加密可并行(因为可以提前对IV进行加密操作)
- 没有错误扩散, 密文中单个比特错误只会导致明文中单个比特错误
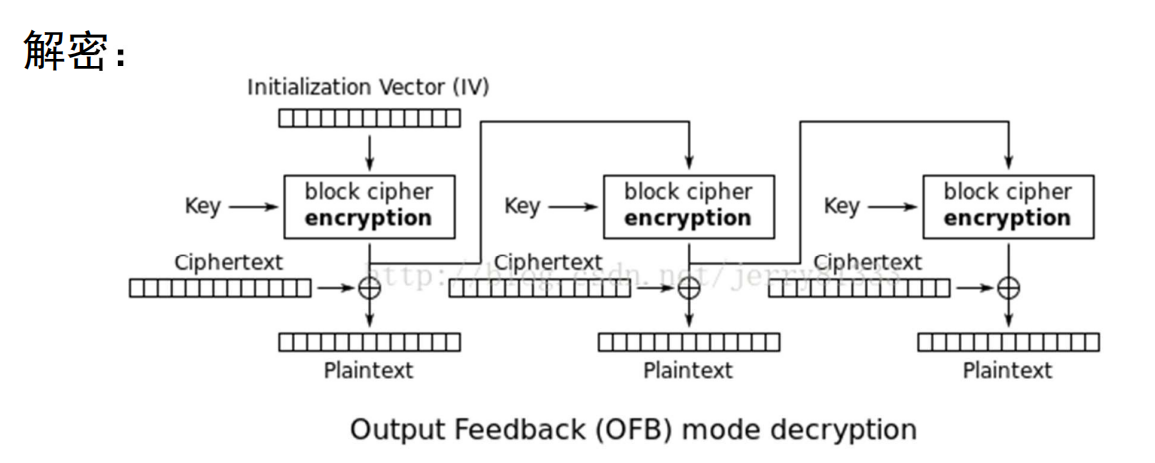
注意
这种方式与前一种密文反馈模式的区别在于它直接拿加密完的密文去参与下一个分组的加密过程了, 因此, 下一个分组的加密与前一个分组的明文就完全无关了.
同样要注意整个过程不涉及到Decryption函数.
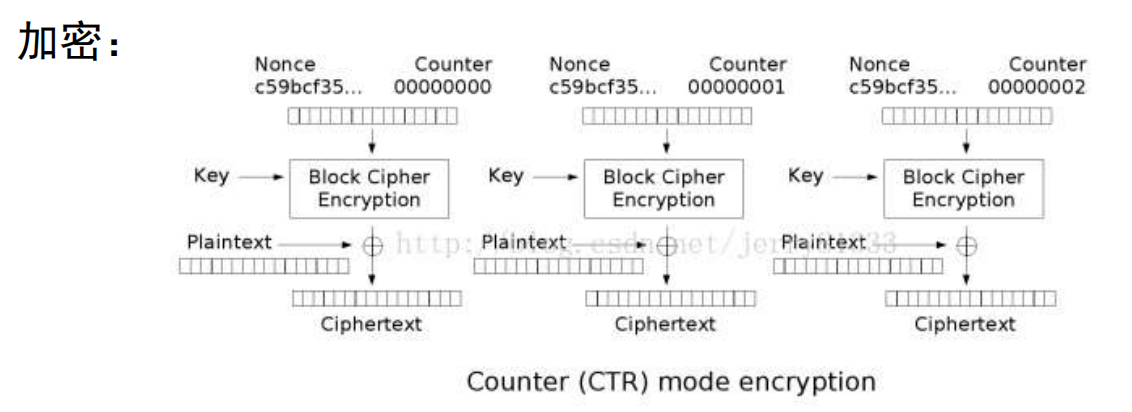
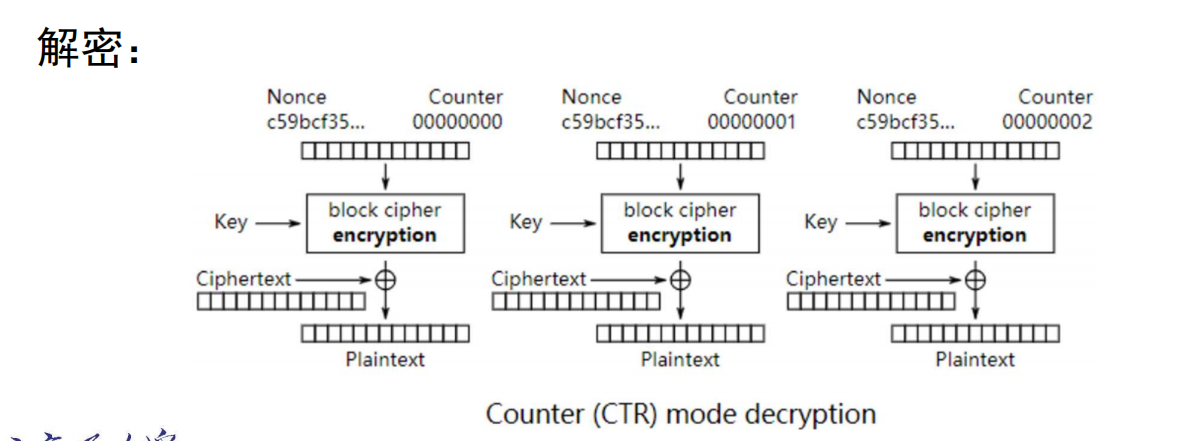
计数器模式(CTR)通过递增一个加密计数器产生连续的密钥流. 随后其余过程与OFB类似.
- 可并行, 可预处理, 高效
- 可以随意加密 / 解密任意一个分组
3.2.3 分组密码的填充
在分组密码中, 常见数据长度不够长的情况, 此时会进行填充. 有如下填充策略, 读者感兴趣请自行了解, 这里不费笔墨了:
- ANSI X9.23
- ISO 10126
- ISO/IEC 7816-4
3.3 非对称加密
非对称加密指的是创建一对密钥, <公钥, 私钥>(<PK, SK>), 加密时用对方的公钥加密, 对方收到后用自己的私钥解密.
3.3.1 RSA算法
该算法的数学基础在于数论:
寻求两个大素数比较简单, 但是将它们的乘积进行分解(即逆向求得这两个大素数)却异常困难. 这就是RSA的 陷门函数 .
RSA的算法过程如下:
- 选取两个不同的大素数 $ p, q $
- 计算 $ n = pq $ (公开), $ \phi(n) = (p-1)(q-1) $ (保密)
- 随机选取整数 $ e $ , 使得 $ gcd(\phi(n), e) = 1 $ (公开)
- 计算d, 满足 $ ed \equiv 1(mod \space \phi(n)) $ (保密)
将整数e作为公钥, 整数d作为私钥.
加密过程: $ C = M^e \space mod \space n $
解密过程: $ P = C^d \space mod \space n $
这其中涉及到一些数论的内容, 读者感兴趣可以去自行了解一下, 也可以看本博客的信安数学基础总结章.