数据库系统概论-Chap.6

数据库系统概论 Database
Study Notes 计算机专业课总复习篇
发布日期:   2025-06-14
更新日期:   2025-06-14
文章字数:   4.2k

Chap.6 关系数据理论

6.1 问题引入

我们在此前的章节中将数据库的定义, 操作, 完整性保障等方面都说完了, 但是好像一直没有说一个比较核心的问题: 到底该怎么设计出一个合理, 优秀的关系模式 ?

啥意思呢, 比如我们要存储学生的成绩, 我们此前一直使用学生表 / 课程表 / 成绩表三个表来存储, 那我为什么不放进一个表里? 一个表存所有的东西, 不好吗?
这就是我们这一章要讨论的.

我们考虑我们需要做到的目标:

  • 能较好地反映现实世界
  • 有良好的操作性能

我们该怎么解决这个问题? 需要先回到第二章中 关系模型 的定义中去.

6.1.1 Re: 关系模型的定义

$$ R(U, D, DOM, F) $$

  • R: 关系名
  • U: 组成该关系的属性名集合
  • D: 该关系属性来自的域
  • DOM: 属性向域的映射集合
  • F: 属性间数据的依赖关系的集合

6.1.2 数据依赖

我们对于数据依赖的定义为:

一个关系内部属性与属性之间的一种约束关系.

其主要类型包括:

  • 函数依赖(Functional Dependency, FD)
  • 多值依赖(Multi-Valued Dependency, MVD)

我们一个个说.

函数依赖(FD)

函数依赖的含义是: 某一个属性的值能被另一个属性唯一确定下来. 通常表现为:

$$ y = f(x) $$

这么写有点抽象, 我们举个例子:
我们之前写的学生表中, Sno是主键, 只要有Sno, 那么学生姓名 / 性别 / 专业等信息都能唯一确定对吧. 那就可以写成:

$$
\begin{align*}
Sname = f(Sno) \\
Ssex = f(Sno) \\
Sdept = f(Sno) \\
…
\end{align*}
$$

这个关系依赖其实挺好的, 但是读者可能目前体会不太到, 没关系, 我们现在举一个不是那么好的例子:
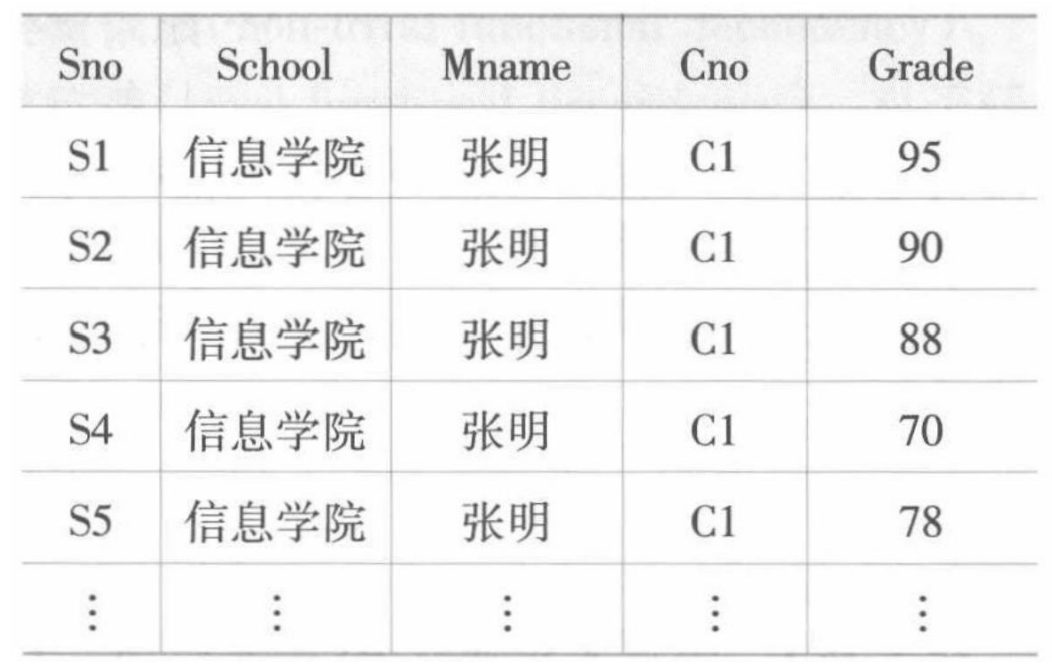
考虑这样一个关系模式的属性集合: $ U = { Sno, School, Mname, Cno, Grade } $

  • Sno: 学号
  • School: 学院
  • Mname: 学院院长
  • Cno: 课程号
  • Grade: 成绩

我们寻思一下这个模式的关系依赖关系:

$$ F = { Sno \to School, School \to Mname, (Sno, Cno) \to Grade } $$

这样看起来还是不够直观, 我们直接列出来就能知道了:

不够完善的数据依赖关系

这个数据关系显然有点问题:

  • 数据冗余 : 院长名出现次数过多
  • 更新异常 : 更换院长后, 一定会导致很多元组跟着一起改
  • 插入异常 : 如果一个学院还没有学生, 就没法将这个学院插入这个表
  • 删除异常 : 如果要给学院的学生全毕业了, 则需要把院长的信息一并删除

怎么改进呢?
我们直觉上, 觉得可以分成以下三个关系模式:

  • $ S(Sno,School, Sno \to School) $
  • $ SC(Sno,Cno,Grade, (Sno,Cno) \to Grade) $
  • $ DEPT(School,Mname, School \to Mname); $

6.2 规范化

6.2.1 函数依赖

6.2.1.1 函数依赖概述

我们的规范化工作极其依赖于我们对于函数依赖的判断. 因此在这里统一一下表示方法:
很复杂的定义我们就不写了, 说白了就是X如果能唯一确定Y, 就写成 $ X \to Y $

给个例子吧, 看这个关系模式: Student(Sno, Sname, Ssex, Sage, School), 假设没有重名学生, 则存在:

$$
\begin{matrix}
& Sno \to Ssex & Sno \to Sage & Sno \to School \\
& Sno \to Sname & Sname \to Sno & Sname \to Ssex \\
& Sname \to School & Sname \to Sage
\end{matrix}
$$

注意
还请读者明确, 一个函数依赖的前后并不一定是唯一一个属性, 它是一个属性集合.

6.2.1.2 平凡函数依赖 / 非平凡函数依赖

所谓平凡 / 非平凡, 其实就是标识一个函数依赖的特殊性. 啥意思呢?
假如Y属性集合本身是X属性集合的子集, 那我说 $ X \to Y $ , 这其实是一句废话. 这种情况我们称这个属性依赖是平凡的.
举个例子就是 $ Sname, Sno \to Sno $ , 废话, 知道前面两个肯定能唯一确定后面那个对吧.

只有Y属性不是X的子集, 但X却能决定Y时, 这时候这个函数依赖才有研究的价值, 我们称这种依赖叫 非平凡函数依赖 .

6.2.1.3 完全函数依赖 / 部分函数依赖

这俩概念在理解前面那个平凡的例子之后就很好解释.

完全函数依赖 的意思是, 假如 $ X \to Y $ , 并且X少了任意一个元素, 就无法唯一确定Y了, 就称 Y 完全依赖于 X .
比如 $ (Sno, Cno) \to Grade $ , 学生号和课程号少一个都不行.
记作:

$$ X \overset{F}{\to} Y $$

部分函数依赖 就是Y只依赖于X这个属性集中的部分属性. 比如: $ (Sno, Sname) \to Sname $ , 这种情况下, 知道Sname(X的)就能知道Sname(Y).
记作:

$$ X \overset{P}{\to} Y $$

6.2.1.4 传递函数依赖

如果 $ X \to Y $ , 而X不依赖于Y; $ Y \to Z $ , 而Y不依赖于Z, 则称 Z 传递依赖 于 X .记作:

$$ X \overset{T}{\to} Z $$

6.2.2 码

我们其实之前给过码的定义:

  • 码 : 能够 唯一标识 一个元组的一个 属性集
    • 这种属性集不一定只有一个, 因此每一个这种属性集都叫 候选码 .
    • 码不一定只有一个属性.
    • 码内的所有属性叫做 主属性 .
    • 不再码内的属性叫做 非主属性 .

我们这里用关系数据理论给一个更加严谨的定义:

对于R<U, F>关系模式, 找到其中的一个属性集(也可以是单个属性)K, 如果 $ K \overset{F}{\to} U $ (即K能 正好 唯一确定整个关系模型中的每一个属性) , 称K是R的一个 候选码 .

如果 $ K \overset{P}{\to} U $ , 则说明K中属性多了(去掉部分属性也能唯一确定整个元组), 这时候称K为 超码 .

如果一个关系模式有多个候选码, 就要从其中选一个作为 主码 .
特殊的, 如果整个属性组是主码, 称为 全码 .

外码 我们也给过:

  • 外码(外键) : 如果某个属性不是本关系的主码, 而是另一个关系的主码, 称之为本关系的外键.

6.2.3 范式

范式 是我们这一章中新的概念.

关系数据库中的关系必须满足一定的要求. 满足不同程度要求的为不同范式.

范式有以下几个种类:

  • 第一范式: (1NF)
  • 第二范式: (2NF)
  • 第三范式: (3NF)
  • BC范式: (BCNF)
  • 第四范式: (4NF)

它们对于数据库的要求是逐层增加的.

范式

6.2.4 1NF

1NF, 即第一范式, 这是关系型数据库的基本要求, 即 所有属性的取值都是原子值, 不可再分 .
用通俗易懂的话说, 就是不能有属性的取值是 集合 .\

给个反例:

学号姓名电话号码
001张三13800000000, 13900000000

把它改成 1NF:

学号姓名电话号码
001张三13800000000
001张三13900000000

6.2.5 2NF

2NF, 即第二范式, 它的本质是 消除了非主属性对于主码的部分依赖

举个例子:

$$ S-L-C(Sno,School,Sloc,Cno,Grade) $$

其中

  • 主键: $ (Sno, Cno) $
  • School: 学院
  • Sloc: 学院地址
  • Grade: 成绩

显然, 这个例子中存在这样的部分依赖关系:
$ School \overset{P}{\to} (Sno, Cno) $
$ Sloc \overset{P}{\to} (Sno, Cno) $

我们要将其改为这样的关系模式:

  • $ SC(\underline{Sno,Cno} ,Grade) $
  • $ S-L(\underline{Sno} ,School,Sloc) $

6.2.6 3NF

3NF, 即三级范式, 本质上是 消除了非主属性对主码的传递函数依赖

我们考虑上面2NF的例子, 会发现有这样的传递关系:
$ Sno \overset{T}{\to} Sloc $

这是因为 $ Sno \to School, School \to Sloc $
因此我们还要改, 把这俩也拆开:

  • $ S-S(Sno,School) $
  • $ S-SL(School,Sloc) $

6.2.7 BCNF

BCNF, 是3NF的更严格版本.
其防止的是: 存在某个决定因素不是候选键，但它却决定了某些属性

换一种更加严格的说法: 消除主属性对码的部分和传递函数依赖

举个例子: $ STJ(S,T,J) $ , 其中:

  • S: 学生, 学生选定某门课, 则能够得到对应的教师
  • T: 教师, 一个教师只教授一门课.
  • J: 课程, 每门课有若干教师

因此, 存在这样的关系:
$ (S, J) \to T $
$ (S, T) \to J $
$ T \to J $ (因为一个老师只教一门课)

这就出问题了, 因为T能决定J, 但是T 不是候选键 (无法决定一整个元组)

这样的情况下, 如果要满足BCNF:

  • ST(S,T)
  • TJ(T,J)

6.2.8 多值依赖

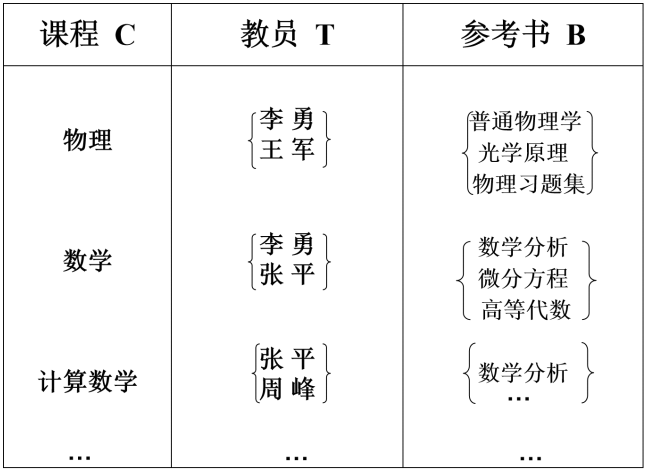
多值依赖是一个更加抽象的概念, 我们从一个例子讲起:
考虑这个关系模型: Teaching(C,T,B), 其中:

  • C: 课程
    • 物理
    • 数学
  • T: 教师
    • 李勇
    • 王军
    • 张平
  • B: 参考书
    • 普通物理学
    • 光学原理
    • 物理习题集
    • 数学分析
    • 微分方程
    • 高等代数

这三个属性之间有这么个关系:

多值依赖例

可以得到这样一个表:

课程C教师T参考书B
物 理李 勇普通物理学
物 理李 勇光学原理
物 理李 勇物理习题集
物 理王 军普通物理学
物 理王 军光学原理
物 理王 军物理习题集
………

我们寻思一下这玩意好像确实符合刚刚说的BCNF, 因为理论上这个表的主键就是它的属性全集(只有三个玩意才能唯一确定一行).
但它问题在哪? 我们发现对于同一门课, 一个参考书集合要在不同的老师中出现好几次, 这显然是一种空间浪费.

这种就叫做 多值依赖 . 其定义如下:

存在三个属性X / Y / Z, 其中X决定了Y的多个取值, 而Y和Z又相互独立(即他们之间可以出现全排列).

多值依赖还分为:

  • 平凡多值依赖: 即虽然X决定了Y的多个取值, 但是这个表里面没有其它属性了(Z是空集).
  • 非平凡多值依赖: X决定了Y的多个取值, 并且表中还有其它与Y独立的属性集.

上表中, 对于课程C, 教师T总是有一个固定的集合与之对应, 但是参考书B却跟教师T毫无关系.
反过来也一样, 对于课程C, 参考书B总是有一个固定的集合与之对应, 但是教师T却跟参考书B毫无关系.

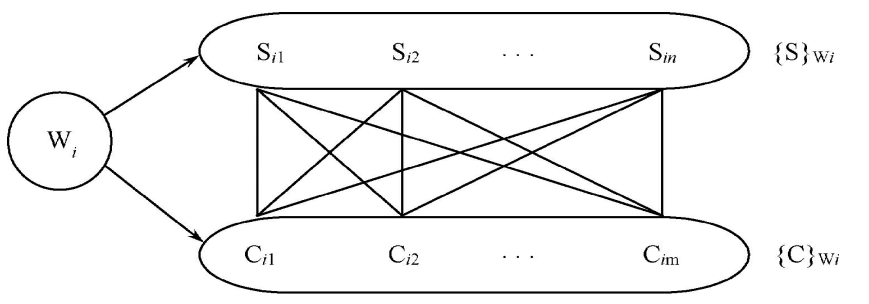
给个图读者应该能更明白一点:

多值依赖示意图

实际上, 函数依赖 其实是多值依赖的一种特殊情况.
函数依赖的意思是, X能够唯一确认Y; 多值依赖的意思是, X能够唯一确认Y的取值集合.
所以事实上, 函数依赖就是 多值依赖集合只有唯一一个元素的情况

读者可以这样理解多值依赖, 即假如有 $ A \to \to B $ , 则除了A, B的其余属性组成的一整个属性集C, 必须出现所有 C能够取到的全部可能性与B的全部可能性任意组合的全部元组 .

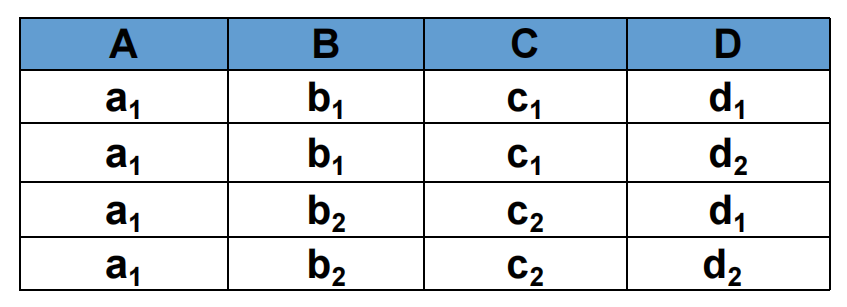
给个例子, 解释一下:

多值依赖例(2)

在这个案例里面:

  • $ A \to \to BC $ 是成立的.
    • 因为 BC 两个属性集, 其在这个表中的取值就两种: $ ( (b_1, c_1), (b_2, c_2) ) $
    • 而对于剩余的这D属性集, 取值也有两种: $ (d_1, d_2) $
    • 而这个表把上面这 2*2 = 4 种可能性都列出来了.
  • $ A \to \to B $ 是不成立的.
    • B有两种取值 $ (b_1, b_2) $
    • CD有四种取值 $ ((c_1, d_1), (c_1, d_2), (c_2, d_1), (c_2, d_2)) $
    • 显然, 上面这两组的全排列有 2*4 = 8种可能, 但是表里只出现了4种. 因此这个多值依赖不成立.

6.2.9 4NF

4NF, 即四级范式, 是基于多值依赖来说的.
它要求, 模式中没有非平凡非函数依赖的多值依赖.

因此, 我们拆解BCNF到4NF的方式就很简单了, 对于每个多值依赖, 把它拆成只有多值依赖的双方组成的一个表即可.

拿上面的课程C-教师T-辅导书B举例子:
由于 $ C \to \to T, C \to \to B $ , 那我们把它拆成两个表即可:

$ CT( \underline{C, T} ) $
$ CB( \underline{C, B} ) $

这两个表虽然多值依赖仍然存在, 但是只有依赖方和被依赖方, 没有第三方, 就符合4NF的要求了.(只有平凡多值依赖)

4.2.10 规范化总结

规范化的过程讨论到 4NF , 基本上就结束了.
其根本目的其实就是消除关系模式中不可以的关系依赖. 我们回顾一下整个过程:

  • 1NF: 基本要求, 不能有能再次拆开的属性
  • 2NF: 不能有依赖部分主键的属性, 要拆出去(Sno, Cno, School , Grade)
  • 3NF: 不能有间接依赖主键的属性, 要拆出去(Sno, School, Place )
  • BCNF: 不能有决定别的属性, 但是不是主键的属性.
  • 4NF: 不能有相互独立的两个属性集, 都多值依赖于主键.

注意
我们上面说的都是理论, 现实中并不是规范化程度越高越好.
因为规范化程度越高, 则数据分散性越高(因为一直在拆表嘛), 这会造成很严重的连接复杂化.
通常现实中只要做到 3NF 即可, 少部分要进一步做到 BCNF

6.3 数据依赖的公理系统

6.3.1 逻辑蕴含

有人为了这个数据依赖定义了一个公理系统, 并给出了一些结论.
我们还是把定义先写出来:

$$ R(U, D, DOM, F) $$

  • R: 关系名
  • U: 组成该关系的属性名集合
  • D: 该关系属性来自的域
  • DOM: 属性向域的映射集合
  • F: 属性间数据的依赖关系的集合

这里只关注 R(U, F), 即属性集合和依赖集合.
这个依赖集合中, 全体函数依赖关系叫做 F的闭包 , 记作 $ F^+ $ , 是个非常庞大的概念.

比如, 有R= (A,B,C), F={A→B, B→C}, 则 $ F^+ $ 有这么多:

F的闭包

6.3.2 ArmStrong 公理系统

为了能够系统的推导一下某些关系, 有人给出了这么个公理系统:

  • 自反律(reflexivity) : 如果属性集 $ Y \subseteq X \subseteq U $ , 则 $ X \to Y $ 一定在F中.(说白了就是X这个属性集已经包含Y的属性了, 那一组X一定可以唯一确定Y)
  • 增广律(augmentation) : 如果 $ X \to Y $ 在F中, 那 $ XZ \to YZ $ 一定也在F中.(左右加上了同样的属性集, 肯定还是成立的)
  • 传递律(transitivity) : 如果 $ X \to Y, Y \to Z $ 在F中, 那 $ X \to Z $ 一定在F中

还有三条导出规则:

  • 合并规则(union rule) : 如果 $ X \to Y, X \to Z $ 则 $ X \to YZ $
  • 伪传递规则(pseudo transitivity rule) : 如果 $ X \to Y, YW \to Z $ , 则 $ XW \to Z $
  • 分解规则(decomposition rule) : 如果 $ X \to Y, Z \subseteq Y $ , 则 $ X \to Z $

相信有了上面的铺垫, 这三条对于读者而言不是很难理解, 不举例子了.

这玩意为啥需要单拿出来呢? 因为有过证明(具体咋整的咱就别管了), 这个公理系统:

  • 有效(即通过F出发, 由ArmString得到的每个函数依赖肯定都在 $ F^+ $ 中)
  • 完备(即 $ F^+ $ 中的每一个函数依赖, 一定能通过F和ArmStrong推出来)

6.3.3 最小依赖集

说了半天, 其实关键还是这个F, 这是个啥呢?
说白了就是这最好是个 最小依赖集 , 它包括几个特点:

  • 这个集合中每一个依赖的右侧部分都只是一个属性.
  • 这个集合中的依赖应该能够推导出全部的 $ F^+ $ , 是说白了就是不能漏掉任何一个必要的依赖.
  • 在这个集合中的依赖不要任何的多余依赖

最小依赖集

本章其实ArmStrong只是一个理论上的东西, 它更多的是针对数据库本身的一些结构化操作而言的, 对于做题不是非常的重要. 理解即可.

最重要的是掌握怎么进行模式分解. 尤其是分解到3NF / BCNF的过程.

文章作者: MUG-chen
文章链接: http://mug-chen.github.io/posts/2069.html
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 MUG-chen !
数据库系统概论 Database
  目录